- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математическая игра 500 или 5х5
Содержание
- 2. Отборочный турИгрокам необходимо на листке написать ответы к предоставленным заданиям.
- 3. Задание 1. Найти ∠С в ∆АВС если:ВАСАВВВААССС50˚75˚70˚70˚50˚90˚ 5226
- 4. Задание 2. Какие утверждения верны?1) Все прямоугольные
- 5. Задание 3,4. Найти необходимые элементы треугольника, если…
- 6. Задание 5. Найти недостающий элемент прямоугольного треугольника.аbсa
- 7. Задание 6,7,8,9,10.Задание 6. Расположить в порядке увеличения
- 8. raaРадиус окружностиДлину окружностиСторону квадрата, вписанного в окружностьСторону правильного шестиугольника, вписанного в окружность
- 9. Тур первыйЗа каждый правильный ответ игрокам дается 1 балл
- 10. 1 Сколько прямых можно провести через 2
- 11. 4 Единственную плоскость можно всегда провести через:а)
- 12. 7 α⋂β=m. Существует ли третья плоскость γ
- 13. 10 Даны 4 точки: А, В, С
- 14. 13 Через три данные точки проведены
- 15. Тур второйЗа каждый правильный ответ игрокам дается 2 балла
- 16. 1 Диагонали прямоугольника принадлежат плоскости α. Сколько
- 17. 4 Плоскости α и р пересекаются
- 18. 7 Прямая проходит через центры вписанной и
- 19. 9 β - плоскость. Точка B
- 20. Тур третий За каждый правильный ответ игрокам дается 5 баллов
- 21. 2 На рисунке
- 22. 6 На рис. - куб.
- 23. Тур четвертыйЗа каждый правильный ответ игрокам дается 10 баллов
- 24. А1ВСЕDАВ1С1D13 Сколько граней куба содержат одновременно точки
- 25. Тур пятый За каждый правильный ответ игрокам дается 25 баллов
- 26. АDСВА1В1С1D1МN1 Сколько общих точек имеют плоскости АВС
- 27. Тур шестойЗа каждый правильный ответ игрокам дается 50 баллов
- 28. D1С1СNМА1В1АВD3 Прямые АС1 и B1Dа) параллельны; с) скрещивающиеся;в)
- 29. Тур седьмойЗа каждый правильный ответ игрокам дается 100 баллов
- 30. 1 Сколько в кубе ребер, пересекающих одно
- 31. 3 Плоскостям скольких граней куба принадлежит точка
- 32. 6 Сколько имеется ребер у куба, скрещивающихся
- 33. Тур восьмойЗа каждый правильный ответ игрокам дается 250 баллов
- 34. В заданиях 1-8 построить точку пересечения прямой
- 35. Тур девятыйЗа каждый правильный ответ игрокам дается 500 баллов
- 37. Скачать презентацию
- 38. Похожие презентации




























![Математическая игра 500 или 5х5 3 Плоскостям скольких граней куба принадлежит точка К?а] 1; с)3;в12: д]4.4 Построить точку пересечения](/img/tmb/13/1266184/5916f855fd6053464c7aad6b729a67d1-720x.jpg)





Слайд 4
Задание 2. Какие утверждения верны?
1) Все прямоугольные равнобедренные
треугольники подобны
2) Все равнобедренные треугольники подобны
3)Все равносторонние треугольники подобны
4)
Все прямоугольные треугольники, имеющие угол в 53˚, подобныОтветы располагать согласно последовательности заданных вопросов
Слайд 5
Задание 3,4.
Найти необходимые элементы треугольника, если…
(рисунок
представлен на доске)
∆АВС=∆МКР если…
∠А=∠М, ∠В=∠К
АВ=МК, АС=МР
АВ=МК, ∠А=∠М
∠А=∠М, ∠С=∠Р, АС=МР
Определить
верное(ые) утверждения
Слайд 6
Задание 5. Найти недостающий элемент прямоугольного треугольника.
а
b
с
a =
5, b = 12
2) c = 13, b =
123) a = b = 3
4) a = b, c = 3
Слайд 7
Задание 6,7,8,9,10.
Задание 6. Расположить в порядке увеличения длины
сторон правильного тре-, десяти-, двадцати-, тридцатиугольника, вписанных в одну
окружностьЗадание 7. Перечислить 3 свойства диагоналей ромба
Задание 8. В параллелограмме одна сторона равна 5, а высота, опущенная на смежную с ней сторону, равна 3. Найти синус каждого из 4 углов параллелограмма. (рисунок представлен на доске).
Задание 9. Написать 4 геометрических термина начинающихся на букву «Т».
Задние 10. написать 4 слова, составленных из букв слова «перпендикуляр».
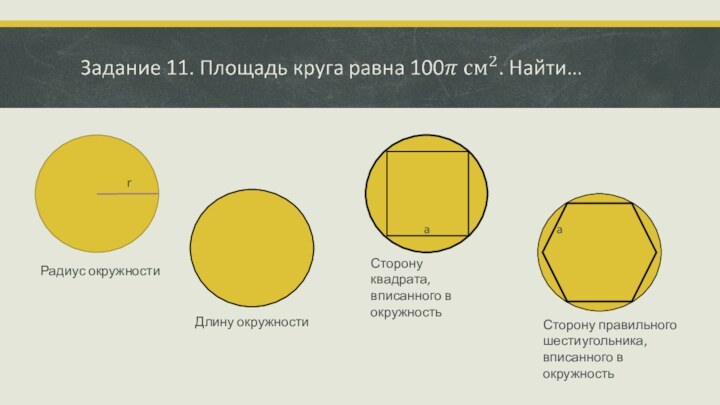
Слайд 8
r
a
a
Радиус окружности
Длину окружности
Сторону квадрата, вписанного в окружность
Сторону правильного
шестиугольника, вписанного в окружность
Слайд 10 1 Сколько прямых можно провести через 2 различные
точки?
а) только одну: с) сколько угодно;
в) только две; д) не всегда
можно.2 Сколько общих точек могут иметь 2 различные плоскости?
а) только одну; с) только три;
в) только две; д) бесчисленное множество.
3 Закончите предложение:
Через 2 прямые нельзя провести плоскость, если они:
а) пересекаются; c) скрещивающиеся;
В) параллельны; д) совладают.
Слайд 11
4 Единственную плоскость можно всегда провести через:
а) одну
прямую; с) прямую и точку вне ее;
в) прямую и точку
на ней; д) прямую и 2 точки вне ее.5 Даны две произвольные точки, через них всегда:
а) нельзя провести плоскость;
в) можно провести единственную плоскость;
с) можно провести ровно две плоскости;
д) можно провести сколько угодно плоскостей.
6 Точки А, В, Си D не лежат в одной плоскости. При этом:
а) каждые 2 из них не лежат на одной прямой;
в) каждые 3 из них не лежат на одной прямой;
с) все лежат На разных прямых;
д) все лежат на одной прямой.
Слайд 12 7 α⋂β=m. Существует ли третья плоскость γ такая,
что m⊂ γ?
а) не существует; с) существуют
2 такие плоскости; в) существует, причем единственная; д) их бесчисленное множество.
8 Прямая b пересекает плоскость β в точке В, прямая а не проходит через точку В, но лежит в плоскости β. При этом:
а) не существует прямая a; c) а и b – скрещивающиеся;
в) а||b; д) а и b - пересекаются.
9 АВСО - параллелограмм. Через две его вершины А, В и точку пересечения диагоналей надо провести плоскость. При этом условии:
а) нет такой плоскости;
в) только 2 вершины параллелограмма лежат в этой плоскости;
с) только 3 вершины параллелограмма лежат в этой плоскости;
д) все вершины параллелограмма лежат в этой плоскости.
Слайд 13 10 Даны 4 точки: А, В, С и
D, не лежащие в одной плоскости. При этом прямые
АС и BD:а) параллельны; с) скрещивающиеся;
в) пересекаются; д) совпадают.
11 Прямая b параллельна плоскости α и лежит в плоскости β. Плоскости α и β пересекаются по прямой т. При этом:
a) b ll m: с) b и m пересекаются;
в) b и m - скрещивающиеся; д) всякое может быть.
12 В плоскости даны 2 пересекающиеся прямые.
Надо провести прямую через точку их пересечения. При этом:
а) такая прямая не существует;
в) она пересекает данную плоскость;
с) она лежит в этой плоскости;
д) может лежать в этой плоскости, а может ее пересекать.
Слайд 14 13 Через три данные точки проведены три
различные плоскости. При этом эти точки:
а) лежат на одной
прямой; в) лежат на скрещивающихся прямых;
с) лежат на параллельных прямых;
д) такого не может быть.
14 ABCD - трапеция. Сколько существует различных плоскостей, в каждой из которых лежат все вершины трапеции?
а) одна; с) три;
в) две; д)бесчисленное множество.
В ∆АВС ∠С=90˚, О - центр описанной около него окружности. Сколько можно построить плоскостей, содержащих точки А, В и О, но не содержащих точку С?
а) нет таких плоскостей; с) две;
в) одну; д) бесчисленное множество.
Слайд 16 1 Диагонали прямоугольника принадлежат плоскости α. Сколько вершин
его лежат в этой плоскости?
а) 1; в) 3;
в) 2; д) 4.
2
Закончите предложение: две прямые являются скрещивающимися, если:а) они не параллельны; с) они лежат в двух разных плоскостях;
в) они не пересекаются; д) они не лежат в одной плоскости.
3 а и b - прямые, α - плоскость, а || α и b || α. Каково при этом взаимное расположение прямых а и Ь?
а] а || b; с) а и b пересекаются;
в) а и b - скрещивающиеся; д) возможно любое.
Слайд 17 4 Плоскости α и р пересекаются по
прямой m, а - прямая; a ll α, а||β.
Каково взаимное расположение прямых а и m?а) они пересекаются; c) они параллельны;
в) они совпадают; д) они скрещиваются.
5 α и β - плоскости, α || β. Прямая m лежит в плоскости β. Каково взаимное расположение m и α?
a) m II а; с) m ⊂ а;
в) они пересекаются; д) возможны любые ситуации.
6 ∆АВС расположен так, что АВ|| α и АС|| α. Каково взаимное расположение прямой ВС и плоскости α?
а) ВС ⊂ а; с) они пересекаются;
в) ВС II а; д) возможны любые случаи.
Слайд 18 7 Прямая проходит через центры вписанной и описанной
окружностей некоторого треугольника. Каково взаимное расположение этой прямой и
плоскости данного треугольника?а) они пересекаются;
в)они параллельны;
с) либо прямая лежит в плоскости треугольника, либо ее пересекает:
д) возможно любое.
8 Прямая проходит через центр окружности. Сколько общих точек она может иметь с этой окружностью?
а)0; с) 1 или 2;
в) 0 или 2: д) 1 или 3
Слайд 19 9 β - плоскость. Точка B ∈
β , прямая m ⊂ β, но B ∉
m. Сколько можно построить плоскостей, параллельных прямой m и содержащих В?а) нельзя построить; с) 2;
в) 1; д) сколько угодно.
10 Точка К не лежит в плоскости треугольника АВС. Каково взаимное расположение прямых АК и ВС?
а) скрещивающиеся: с) параллельны;
в) пересекающиеся; д) возможно любое.
Слайд 21 2 На рисунке –
куб. При этом примером скрещивающихся прямых являются:
ВС и С1D
3) С1D и ADAB и BC 4) С1D и АВ1
3 Тот же куб. При этом:
А1В1II (AB1C1) 3) BC II (AB1C1)
DD1II (AB1C1) 4) AA 1 II (AB1C1)
4 Тот же куб. При этом параллельными являются прямые:
AD и CC 1 3) AD и C 1D1
AD и BB 1 4) AD и B 1C 1
5 Тот же куб. При этом пересекающимися являются прямые:
C 1D и ВС 3) А1В1 и A 1 D 1
А1В1 и АВ 4) А1В1 и C 1D
1 А – точка, а – прямая, А ∈ а. Сколько прямых, перпендикулярных а, можно провести через точку А?
1) 1 2) 2 3)3 4) бесчисленное множество
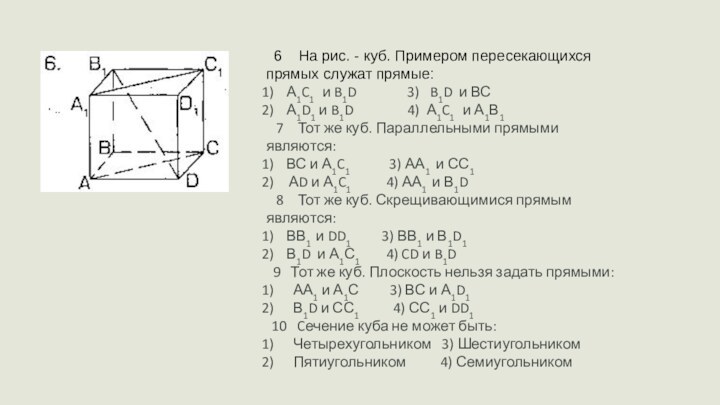
Слайд 22 6 На рис. - куб. Примером
пересекающихся прямых служат прямые:
А1C1 и B1D
3) B1D и ВСА1D1 и B1D 4) А1C1 и А1В1
7 Тот же куб. Параллельными прямыми являются:
ВС и А1C1 3) АА1 и СС1
АD и А1C1 4) АА1 и В1D
8 Тот же куб. Скрещивающимися прямым являются:
ВВ1 и DD1 3) ВВ1 и В1D1
В1D и А1С1 4) CD и B1D
9 Тот же куб. Плоскость нельзя задать прямыми:
АА1 и А1С 3) ВС и А1D1
В1D и СС1 4) СС1 и DD1
10 Cечение куба не может быть:
Четырехугольником 3) Шестиугольником
Пятиугольником 4) Семиугольником
Слайд 24
А1
В
С
Е
D
А
В1
С1
D1
3 Сколько граней куба содержат одновременно точки С.
С, и Е?
4 Сколько граней куба содержат одновременно точки
В, С и С1?5 Сколько у куба ребер, параллельных ребру CD?
1 Сколько граней куба содержат В?
2 Сколько граней куба содержат и точку В и точку С?
6 Если провести сечение куба плоскостью, проходящей через точки А1, С и Е, то по какой прямой секущая плоскость пересечет плоскость грани ВВ1С1С
7 Сколько перпендикуляров к данной прямой можно провести через точку, данную вне этой прямой?
Слайд 26
А
D
С
В
А1
В1
С1
D1
М
N
1 Сколько общих точек имеют плоскости АВС и
DB1С1?
2 Сколько общих точек имеют плоскости DD1C1 и DB1С1?
3
В какой точке прямая MN пересекает плоскость ВСС1.4 В какой точке прямая MN пересекает плоскость ADD
5 Найти точку пересечения прямой MN с прямой АВ.
6 Найти точку пересечения прямой MN с прямой А1В1
7 С плоскостями скольких граней куба пересекается прямая C1D?
8 С плоскостями скольких граней куба пересекается прямая B1D1?
9 Плоскости каких граней пересекает прямая А1N. Найдите точки пересечения
10 Назвать прямую, по которой пересекаются плоскости D,MN и АВВ,. 2
Слайд 28
D1
С1
С
N
М
А1
В1
А
В
D
3 Прямые АС1 и B1D
а) параллельны; с) скрещивающиеся;
в) пересекаются: д)
всякое может быть.
4 С помощью рисунка выяснить ответ на
вопрос. Каждая из двух данных прямых является скрещивающейся с третьей. Как при этом могут располагаться две данные прямые?а) скрещивающиеся; с) пересекаются;
в) параллельны; д) всякое может быть.
1 Найти точки пересечения прямых:
1. MN и A1D1; 3. MN и ВС;
2. MN и BD; 4. MD и A1D1.
2 Через точку D плоскости B,C,D проведена прямая, не принадлежащая этой плоскости. Может быть:
а)такой прямой нет; с) это DD1:
в) эto DA; д) это DB,.
5 Сколько всего ребер у куба?
а) 4; с) 8;
в) 6; д) 12.
Слайд 30 1 Сколько в кубе ребер, пересекающих одно какое-либо
ребро?
а) 1; с) 3;
в) 2; д) 4.
Сколько в кубе ребер,
лежащих на прямых, которые с прямой, на которой лежит данное ребро, являются скрещивающимися? а) 2; с) 4;
в) 3; д) 6.
Слайд 31
3 Плоскостям скольких граней куба принадлежит точка К?
а]
1; с)3;
в12: д]4.
4 Построить точку пересечения прямых В, М и ВС.
5
Найти на рисунке ребра куба, скрещивающиеся с DDV но пересекающиеся с ВС.a] CD; cl АВ:
в) АО; д]ВВ,.
Слайд 32 6 Сколько имеется ребер у куба, скрещивающихся с
А1В1 но пересекающих CD?
а) 1; с)3;
в) 2; д)4
7 Построить точку пересечения
прямых КМ и ВС.8 Построить точку пересечения прямых ЕМ и C1D1
9 Построить точку пересечения прямых А1М и АС.
10 Построить точку пересечения прямых КЕ и В1D1
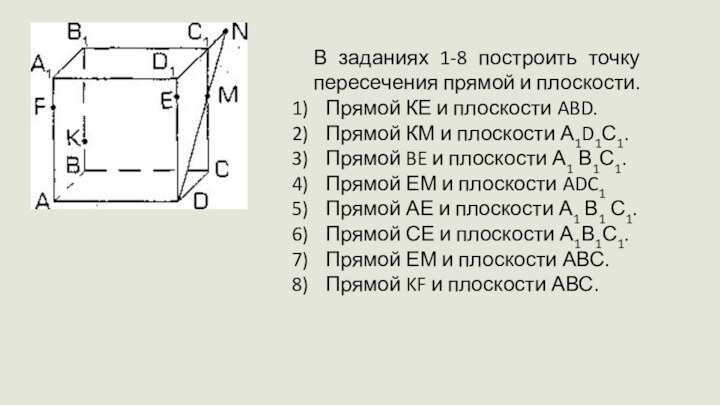
Слайд 34 В заданиях 1-8 построить точку пересечения прямой и
плоскости.
Прямой КЕ и плоскости ABD.
Прямой КМ и плоскости А1D1С1.
Прямой
BE и плоскости А1 В1С1.Прямой ЕМ и плоскости ADC1
Прямой АЕ и плоскости А1 В1 С1.
Прямой СЕ и плоскости А1В1С1.
Прямой ЕМ и плоскости АВС.
Прямой KF и плоскости АВС.





























