- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математические преобразования в МР-томографии
Содержание
- 2. План лекцииДвумерное преобразование ФурьеПреобразование ФурьеТеорема о сверткеФильтрация изображенийПреобразование РадонаПреобразование РадонаТеорема о центральном слоеFiltered back projection
- 3. Одномерное преобразование ФурьеПрямое преобразование сигнал во времени
- 4. Двумерное преобразование ФурьеАналогично одномерному случаю – прямое преобразованиеИ обратное преобразование
- 5. Двумерное дискретное преобразование ФурьеДля дискретного набора данных – прямое преобразованиеИ обратное преобразование
- 6. Двумерное преобразование ФурьеКак и в случае одномерного
- 7. Изображение и его пространственный спектр
- 8. Изображение и его пространственный спектр
- 9. Дискретная двумерная сверткаДля двух дискретных функций свертка
- 10. Связь свертки и преобразования ФурьеТеорема о свертке
- 11. Свертка, как фильтрТак как результатом свертки является
- 12. Ядро усредненияРассмотрим действие ядраИз определения свертки –
- 13. Ядро размытияПримеры действия ядра 3х3 9х9
- 14. Ядро усреднения по ГауссуРассмотрим действие ядраПри выборе
- 15. Усреднение по Гауссу
- 16. Градиент (производная первого порядка)Ядро Превитта (в зависимости от направления взятия производной)Ядро Собеля
- 17. Ядро ПревиттаПримеры действия ядра dx dy
- 18. Ядро СобеляПримеры действия ядра dx dy
- 19. ЛапласианСочетание двух производных второго порядка по двум
- 20. Лапласиан
- 21. Преобразование РадонаПрямое преобразование: переводит двумерную функцию в её интеграл вдоль произвольной оси rθ
- 22. Преобразование РадонаПример преобразования
- 23. Обратное преобразование РадонаОбратное преобразование радона (алгоритм обратной проекции)И его дискретная модель
- 24. Обратное преобразование РадонаТочность реконструкции зависит от числа проекций 5 12 180
- 25. Обратное преобразование РадонаОднако, даже при большом числе
- 26. Теорема о центральном сеченииФурье-преобразование проекции функции на
- 27. Алгоритм отфильтрованной обратной проекцииПредполагает реконструкцию исходного изображения из проекций, прошедших фильтрацию в частотном пространстве
- 28. Алгоритм отфильтрованной обратной проекцииПример преобразования
- 29. Скачать презентацию
- 30. Похожие презентации
План лекцииДвумерное преобразование ФурьеПреобразование ФурьеТеорема о сверткеФильтрация изображенийПреобразование РадонаПреобразование РадонаТеорема о центральном слоеFiltered back projection
























Слайд 2
План лекции
Двумерное преобразование Фурье
Преобразование Фурье
Теорема о свертке
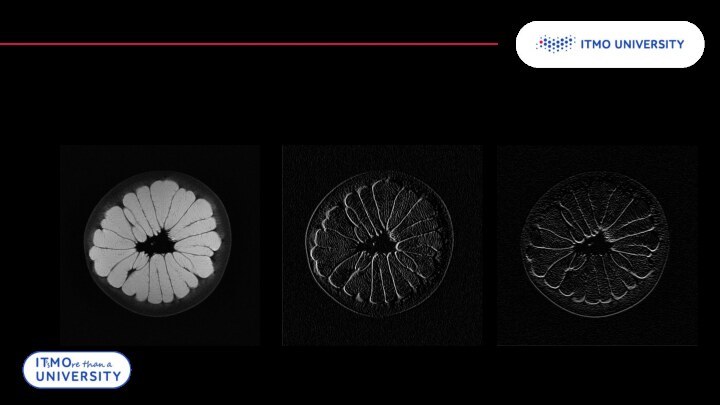
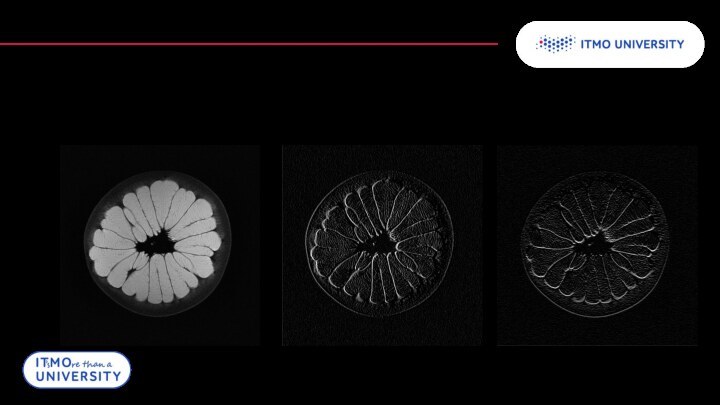
Фильтрация изображений
Преобразование
Радона
Слайд 3
Одномерное преобразование Фурье
Прямое преобразование сигнал во времени в
спектр по частоте
Обратное преобразование переводит спектр в сигнал по
времени
Слайд 4
Двумерное преобразование Фурье
Аналогично одномерному случаю – прямое преобразование
И
обратное преобразование
Слайд 5
Двумерное дискретное преобразование Фурье
Для дискретного набора данных –
прямое преобразование
И обратное преобразование
Слайд 6
Двумерное преобразование Фурье
Как и в случае одномерного преобразования
Фурье, двумерное преобразование является сменой базиса разложения функций
Для одномерного
преобразования – одномерные гармоники, для двумерного - двумерные
Слайд 9
Дискретная двумерная свертка
Для двух дискретных функций свертка определяется,
как
Пределы суммирования могут варьироваться в зависимости от областей определения
функцийСвертка функции представляет собой точки оригинальной функции, взвешенные ядром свертки h
Слайд 11
Свертка, как фильтр
Так как результатом свертки является модификация
каждого значения функции f, то операцию свертки можно использовать
для создания фильтровНапример, для размытия изображения, повышения резкости, поиска краёв изображения и других.
Слайд 12
Ядро усреднения
Рассмотрим действие ядра
Из определения свертки – сопоставит
значению функции значение, усредненное с 8 соседними
В общем случае
Слайд 14
Ядро усреднения по Гауссу
Рассмотрим действие ядра
При выборе большого
σ – фильтр размытия (усреднения)
При малом σ – не
влияет на изображение
Слайд 16
Градиент (производная первого порядка)
Ядро Превитта (в зависимости от
направления взятия производной)
Ядро Собеля
Слайд 19
Лапласиан
Сочетание двух производных второго порядка по двум координатам
Форма
– из численной аппроксимации второй производной для дискретных функций
Слайд 21
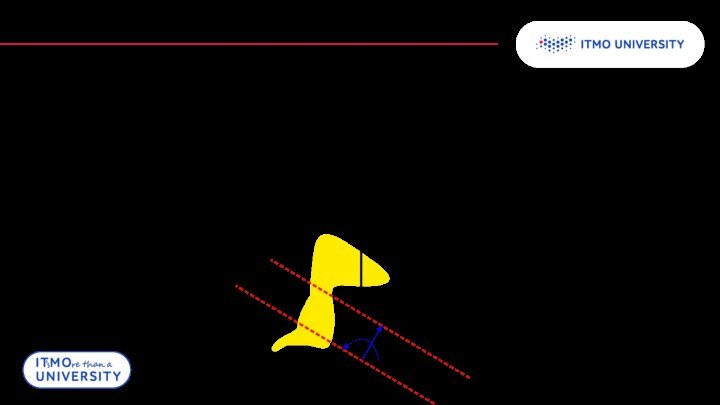
Преобразование Радона
Прямое преобразование: переводит двумерную функцию в её
интеграл вдоль произвольной оси
r
θ
Слайд 23
Обратное преобразование Радона
Обратное преобразование радона (алгоритм обратной проекции)
И
его дискретная модель
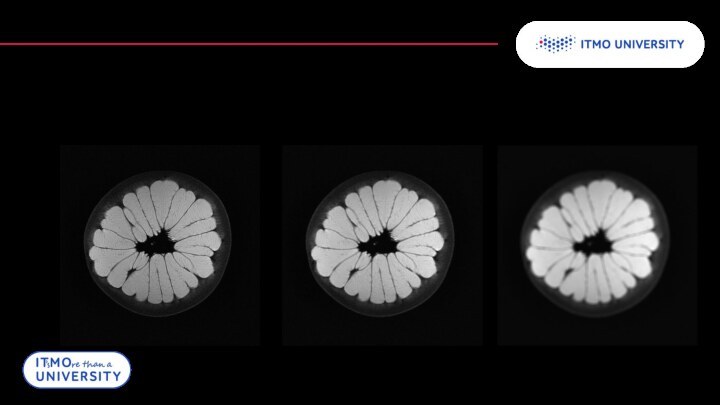
Слайд 25
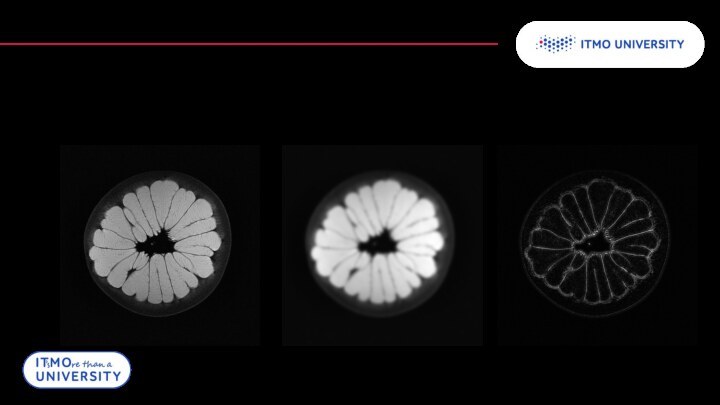
Обратное преобразование Радона
Однако, даже при большом числе проекций
реконструкция получается неточной
Для точечного источника реконструкция имеет вид 1/r
Для
практической реконструкции используется алгоритм отфильтрованой обратной проекции, основанной на теореме центрального сечения
Слайд 26
Теорема о центральном сечении
Фурье-преобразование проекции функции на ось
является Фурье-образом функции вдоль линии, проходящей через центр координат
под углом проекции