- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы решения неравенств с одной переменной (типовые задания С3) - 1
Содержание
- 2. 1. Алгебраические методы решенияЕсли исходить из определения
- 3. 1.1. Сведение неравенства к равносильной системе или
- 4. В общем случае, если решение неравенства не
- 5. Пример 1. (МИОО, 2009). Решите неравенствоРешение. Так
- 6. при x = 2 или x =
- 7. На числовой прямой Ox дано графическое представление
- 8. Пример 2. (МИЭТ, 2000). Решите неравенствоРешение. Выполняя равносильные преобразования данного неравенства, получим:
- 9. Неравенства, содержащие иррациональные выраженияПриведем некоторые стандартные схемы
- 12. Пример 3. Решите неравенствоРешение. Если 2 -
- 13. На рис. представлен способ графической интерпретации получения решения последней системы неравенств. В итоге получаем
- 14. Пример 4. (МИЭТ, 1999). Решите неравенствоРешение. Используя
- 15. Первое неравенство системы (I) приводим к виду:На
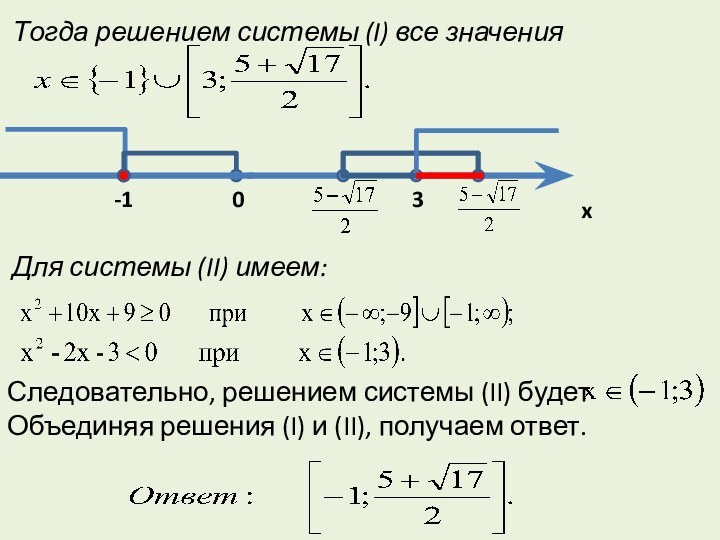
- 16. Тогда решением системы (I) все значения Для
- 17. При решении данного в примере 4 неравенства
- 18. Пусть x2-2x - 3 < 0. Так
- 19. Пример 5. (МИОО, 2009). Решите неравенствоРешение. Выполняя равносильные переходы, получим
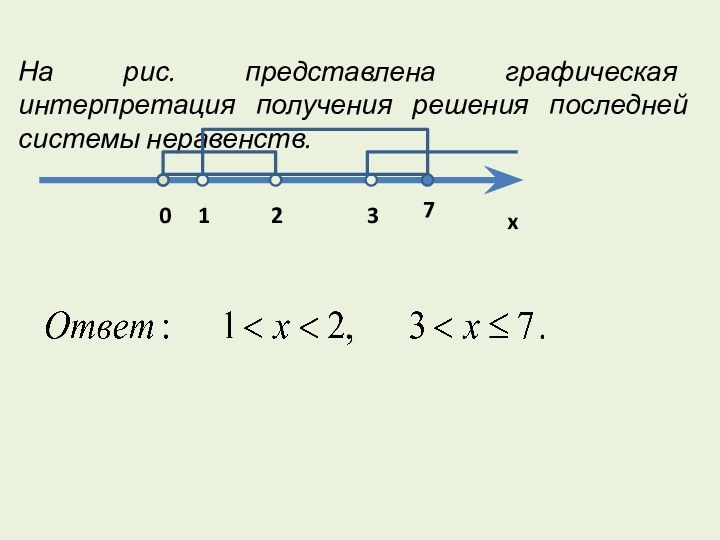
- 20. На рис. представлена графическая интерпретация получения решения последней системы неравенств.
- 21. Пример 6. Решите неравенствоРешение. Обозначим . Тогда выразим
- 22. Возвращаемся к переменной x :
- 23. Пример 7. (МИЭТ, 2002). Решите неравенствоРешение. Область
- 24. Так как на области определения исходного неравенства ,
- 25. На рис. представлена графическая интерпретация получения решения
- 26. Неравенства, содержащие показательные выраженияПриведем некоторые стандартные схемы
- 27. В частности:
- 28. Пример 8. Решите неравенствоРешение. 1-й способ. Область
- 29. Получаем неравенство2-й способ. Так както, используя схему (12), получаем:
- 30. Замечание. При решении неравенства log2(x2-1)
- 31. Пример 9. Решите неравенство (x2 + x +1)x
- 32. При решении данного неравенства использован формальный переход
- 34. Неравенства, содержащие логарифмические выраженияПриведем некоторые стандартные схемы
- 35. ● Если число 0 < a <
- 36. Пример 10. Решите неравенствоlog0.1(x2+x-2)>log0.1(x+3)Решение. Так как основание
- 37. Пример 11. (МИОО, 2009). Решите неравенствоРешение. Выполняя
- 38. На рис. представлена графическая интерпретация получения решения последней системы неравенств.
- 39. Пример 12. (ЕГЭ 2010). Решите неравенствоРешение. В
- 40. Так как при допустимых значениях переменной x
- 41. С учетом области определения данного неравенстваполучаем ответ.
- 42. Неравенства, содержащие выражения с модулямиПример 13. (МИЭТ, 2002). Решите неравенствоРешение. Данное неравенство равносильно совокупности двух систем:
- 44. Приведем некоторые стандартные схемы для решения неравенств
- 45. Пример 14. Решите неравенствоРешение. Используя схему (20)
- 46. Пример 15. Решите неравенствоРешение. Данное неравенство равносильно
- 47. Пример 16. Решите неравенствоРешение. Используя схему (22),
- 48. Для решения неравенств вида:где символ \/ заменяет
- 49. На каждом из промежутков, на которые найденные
- 50. Освобождаясь от знаков модулей, с учетом знаков
- 51. Если , то исходное неравенство равносильно неравенствуx -1+
- 52. Расщепление неравенствЕсли левая часть неравенства представляет собой
- 54. Пример 18. Решите неравенствоРешение. Приведем данное неравенство
- 55. Решим каждое неравенство системы (I).Для неравенства (1) имеем:Для неравенства (2) имеем:
- 56. Значит все значения x принадлежат (0; 1]
- 57. Значит все значения – решения системы (II).Объединяя решения
- 58. Скачать презентацию
- 59. Похожие презентации









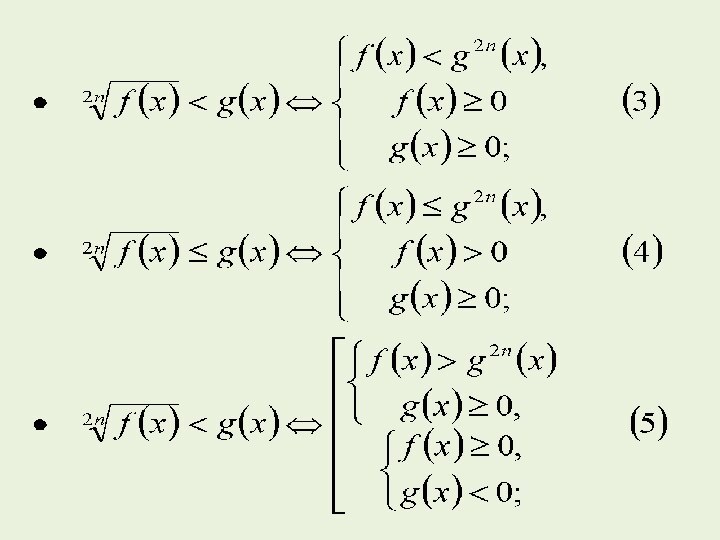



















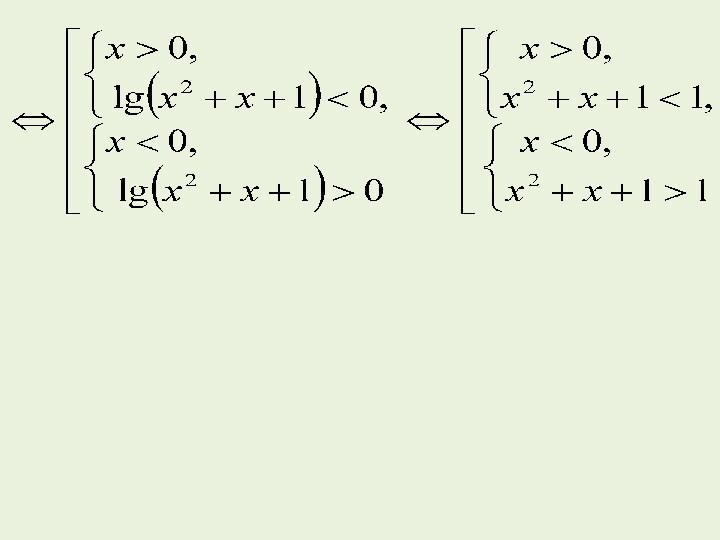



















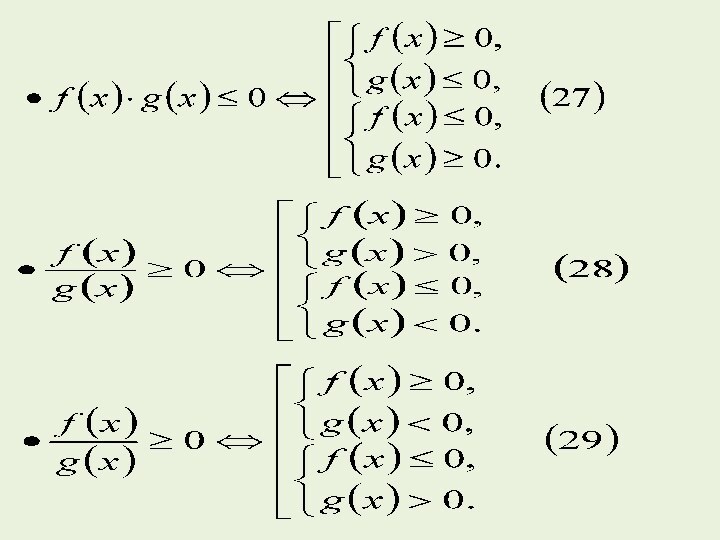


![Методы решения неравенств с одной переменной (типовые задания С3) - 1 Значит все значения x принадлежат (0; 1] – решения системы (I).Найдем решение](/img/tmb/12/1114071/650619a010968c6c599c19669c4e251f-720x.jpg)


Слайд 3 1.1. Сведение неравенства к равносильной системе или совокупности
систем
Как правило, преобразования используют для того, чтобы в неравенстве
освободиться от знаков корней, от знаков модуля, от степеней, от знаков логарифма. Поэтому ниже приведены схемы решения некоторых стандартных неравенств определенного вида. При этом отметим, что на практике некоторые цепочки преобразований делают короче, пропуская некоторые очевидные преобразования. Например, вместо длинной цепочки преобразованийСлайд 4 В общем случае, если решение неравенства не укладывается
в стандартную схему, ход решения разбивают на несколько логически
возможных случаев.
Слайд 5
Пример 1. (МИОО, 2009). Решите неравенство
Решение. Так как
x2 - 6x + 9 = (x-3)2 , то
область допустимых значений переменной x определяется условиями:Исходное неравенство при полученных ограничениях для переменной x равносильно неравенству
Слайд 6 при x = 2 или x = 4
. Значит, с учетом полученных ранее ограничений, x =
2 – решение, так как в этом случае левая часть неравенства (1) равна нулю.Слайд 7 На числовой прямой Ox дано графическое представление решения
последнего неравенства.
Замечание. При решении неравенства
использован метод интервалов.
С
учетом полученных ранее ограничений записываем ответ.
Слайд 8
Пример 2. (МИЭТ, 2000). Решите неравенство
Решение. Выполняя равносильные
преобразования данного неравенства, получим:
Слайд 9
Неравенства, содержащие иррациональные выражения
Приведем некоторые стандартные схемы для
решения иррациональных неравенств, в которых используют возведение в натуральную
степень обеих частей неравенства.
Слайд 12
Пример 3. Решите неравенство
Решение. Если 2 - x
> 0 или 2 - x = 0 ,
то исходное неравенство не выполняется, так какПусть 2 - x > 0 , тогда при возведении обеих частей неравенства в квадрат получим на ее области определения и при условии 2 - x > 0 равносильное неравенство.
Слайд 13 На рис. представлен способ графической интерпретации получения решения
последней системы неравенств. В итоге получаем
Слайд 14
Пример 4. (МИЭТ, 1999). Решите неравенство
Решение. Используя схему
(6), получим, что данное неравенство равносильно совокупности двух систем:
Для
системы (I) имеем:
Слайд 15
Первое неравенство системы (I) приводим к виду:
На числовой
прямой Ox дано графическое представление решения первого неравенства системы
(I).
Слайд 16
Тогда решением системы (I) все значения
Для системы
(II) имеем:
Следовательно, решением системы (II) будет Объединяя решения (I)
и (II), получаем ответ.Слайд 17 При решении данного в примере 4 неравенства использован
формальный переход к равносильной совокупности по схеме (6). Рассмотрим
содержательную сторону этого перехода. Если , то обе части неравенства неотрицательны. После возведения в квадрат обеих частей неравенства получим на его области определения и при условииравносильное не равенство, то есть систему неравенств
Слайд 18 Пусть x2-2x - 3 < 0. Так как ,
то исходное неравенство выполняется на области его определения, т.е.
получаем систему неравенствСлайд 20 На рис. представлена графическая интерпретация получения решения последней
системы неравенств.
Слайд 21
Пример 6. Решите неравенство
Решение. Обозначим . Тогда выразим x
= t 2 + 2 и приведем данное неравенство
к видуТак как t + 2 > 0, то получаем равносильное неравенство 2t 2 + 7 >t 2 + 4t + 4 или t 2 - 4t +3 > 0 при
Отсюда получаем
Слайд 23
Пример 7. (МИЭТ, 2002). Решите неравенство
Решение. Область определения
данного неравенства определяется условиями:
Запишем исходное неравенство в следующем виде
Слайд 24 Так как на области определения исходного неравенства , то,
умножив обе части неравенства (*) на получим неравенство, равносильное
исходному:Левая и правая части последнего неравенства неотрицательны при - 0,5
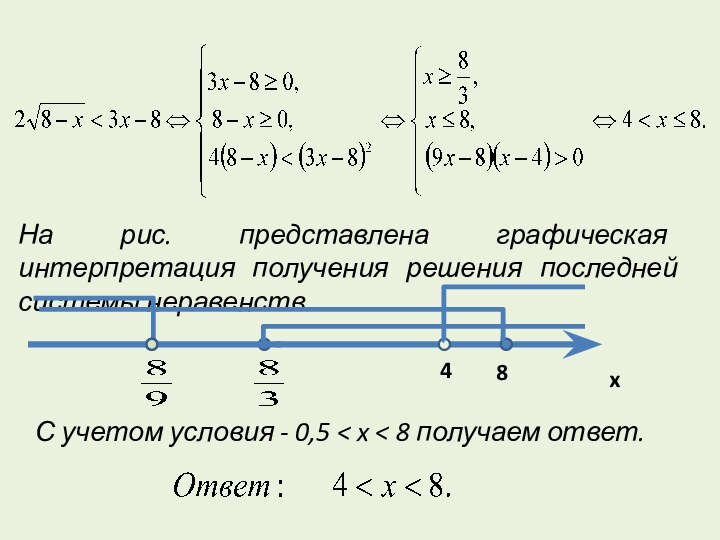
Слайд 25 На рис. представлена графическая интерпретация получения решения последней
системы неравенств.
С учетом условия - 0,5 < x
8 получаем ответ.
Слайд 26
Неравенства, содержащие
показательные выражения
Приведем некоторые стандартные схемы для решения
показательных неравенств, в которых используют логарифмирование обеих частей неравенства.
Слайд 28
Пример 8. Решите неравенство
Решение. 1-й способ. Область допустимых
значений переменной x определяется условием:
При допустимых значениях переменной преобразуем
левую часть данного неравенстваСлайд 30 Замечание. При решении неравенства log2(x2-1)
логарифмических неравенств (см. раздел неравенства, содержащие логарифмические выражения»).
Слайд 31 Пример 9. Решите неравенство (x2 + x +1)x
Решим систему (1) полученной совокупности:
Решим систему (2) совокупности:
Слайд 32 При решении данного неравенства использован формальный переход к
равносильной совокупности по схеме (9). Рассмотрим содержательную сторону этого
перехода. Выражение (x2 + x +1)x положительно, так как x2 + x +1 > 0 при всех значениях x э R . Прологарифмируем обе части данного неравенстваlg(x2 + x +1)x < lg1 x lg(x2 + x +1) <0
Слайд 34
Неравенства, содержащие
логарифмические выражения
Приведем некоторые стандартные схемы для решения
логарифмических неравенств, в которых используют потенцирование обеих частей неравенства.
В
частности:● Если число a >1, то
Слайд 36
Пример 10. Решите неравенство
log0.1(x2+x-2)>log0.1(x+3)
Решение. Так как основание 0,1
логарифмов, стоящих в обеих частях неравенства, удовлетворяют условию
0
< 0,1 < 1, то, используя схему (19), получаем, что данное неравенство равносильно системеНа рис. представлена графическая интерпретация получения решения последней системы неравенств.
Слайд 37
Пример 11. (МИОО, 2009). Решите неравенство
Решение. Выполняя равносильные
переходы, получим, что данное неравенство равносильно следующей системе неравенств
В
соответствии со схемой (17) для решения необходимо рассмотреть только случай, когда основание больше единицы, поэтому полученная система равносильна следующейСлайд 38 На рис. представлена графическая интерпретация получения решения последней
системы неравенств.
Слайд 39
Пример 12. (ЕГЭ 2010). Решите неравенство
Решение. В соответствии
с определением логарифма, входящие в неравенство выражения имеют смысл
при выполнении условий:Слайд 40 Так как при допустимых значениях переменной x по
свойствам логарифма справедливы равенства:
то исходное неравенство приводится к виду
Последнее
неравенство равносильно совокупности двух систем на множестве
Слайд 42
Неравенства, содержащие выражения с модулями
Пример 13. (МИЭТ, 2002).
Решите неравенство
Решение. Данное неравенство равносильно совокупности двух систем:
Слайд 44 Приведем некоторые стандартные схемы для решения неравенств с
модулями, которые опираются на определение модуля, его геометрический смысл
и свойства.
Слайд 45
Пример 14. Решите неравенство
Решение. Используя схему (20) получаем,
что данное неравенство равносильно системе неравенств
или после приведения подобных
членов
Слайд 46
Пример 15. Решите неравенство
Решение. Данное неравенство равносильно следующему
Используя
схему (23), получаем, что это неравенство, а значит и
исходное, равносильно совокупности неравенств
Слайд 47
Пример 16. Решите неравенство
Решение. Используя схему (22), получаем,
что данное неравенство равносильно совокупности неравенств
Используя схемы (20) и
(22), получаем, что эта совокупность равносильна следующей.
Слайд 48
Для решения неравенств вида:
где символ \/ заменяет один
из знаков неравенств: применяют метод промежутков. Для этого находят
ОДЗ неравенства, определяют точки разрыва функций f1(x), f2(x), ……, fn(x) и находят корни совокупности уравненийСлайд 49 На каждом из промежутков, на которые найденные точки
разбивают ОДЗ, функции, стоящие под знаком модуля, имеют постоянный
знак. Поэтому исходное неравенство на каждом промежутке заменяется на неравенство, не содержащее знаков абсолютной величины и равносильное исходному.Пример 17. Решите неравенство
Решение. Решением совокупности
являются числа 1 и 2.
Эти числа разбивают числовую прямую на три промежутка
Слайд 50 Освобождаясь от знаков модулей, с учетом знаков выражений
под знаком модуля решим данное неравенство на каждом из
этих промежутков+
_
Если x<1, то исходное неравенство равносильно неравенству - x +1- x + 2 > 3 + x , x < 0 . Получаем, что x < 0 есть решение исходного неравенства на рассматриваемом промежутке.
Если , то исходное неравенство равносильно неравенству x -1- x + 2 > 3+ x , x <-2 . Следовательно, на этом промежутке решений нет.
Слайд 51
Если , то исходное неравенство равносильно неравенству
x -1+ x
- 2 > 3+ x , x > 6
.Получаем, что x > 6 есть решение исходного уравнения на рассматриваемом
промежутке.
Объединяя полученные решения, запишем ответ.
Слайд 52
Расщепление неравенств
Если левая часть неравенства представляет собой произведение
двух выражений, а правая часть равна нулю, то схема
решения неравенства опирается на правило знаков при умножении (делении) положительных или отрицательных чисел.
Слайд 54
Пример 18. Решите неравенство
Решение. Приведем данное неравенство к
следующему виду:
В соответствии со схемой полученное неравенство равносильно совокупности
систем (I) и (II):Слайд 56 Значит все значения x принадлежат (0; 1] –
решения системы (I).
Найдем решение системы (II). Для неравенства (3),
используя решение (1), имеем:
Слайд 57
Значит все значения – решения системы (II).
Объединяя решения систем
(I) и (II), получаем ответ.
Для неравенства (4), используя решение
(2) и учитывая ограниченияимеем: