Презентация на тему Математические задачи компьютерной томографии

родственное преобразованию Фурье. Впервые введено в работе австрийского математика

Иоганна Радона 1917-го года.

Важнейшее свойство преобразования Радона — обратимость, то есть возможность восстанавливать исходную функцию по её преобразованию Радона.

функции f(x,y)
Формула обращения для двумерного преобразования Фурье
в полярных координатах

z = − xsinα + ycosα.
Таким образом, одномерное

преобразование Фурье по переменной s от преобразования Радона функции f даёт нам двумерное преобразование Фурье от функции f. Формула обращения преобразования Радона

или

.

следующих операций:

* формирования требуемой ширины рентгеновского луча (коллимирование);

* сканирования

объекта пучком рентгеновского излучения, осуществляемого движением (вращательным и поступательным) вокруг пациента устройства излучатель – детекторы;

* измерения излучения и определения его ослабления с последующим преобразованием результатов в цифровую форму;

* машинного (компьютерного) синтеза томограммы по совокупности данных измерения, относящихся к выбранному слою;

* построения изображения исследуемого слоя на экране видеомонитора (дисплея).

пространственной и по перепаду плотности. Первый тип определяется размером

клетки матрицы (1,5 x 1,5 мм), второй равен 5 ед. Н. (0,5 %). В соответствии с этими характеристиками теоретически можно различать элементы изображения размером 1,5 x 1,5 мм. При перепаде плотности между ними не меньше 5 ед. Н. (1 %) удается выявлять очаги величиной не менее 6 x 6 мм, а при разнице в 30 ед. Н. (3 %) — детали размером 3 x 3 мм.

определённая на всей плоскости и достаточно быстро убывающая на

бесконечности (так, чтобы соответствующие несобственные интегралы сходились). Тогда преобразованием Радона функции f(x,y) называется функция

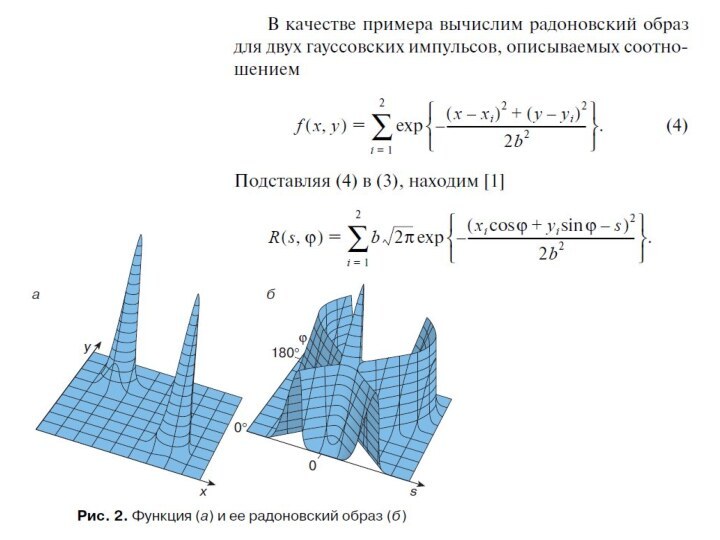
Преобразование Радона имеет простой геометрический смысл — это интеграл от функции вдоль прямой, перпендикулярной вектору n ̅ (АА’) и проходящей на расстоянии s (измеренного вдоль вектора n ̅, с соответствующим знаком) от начала координат.

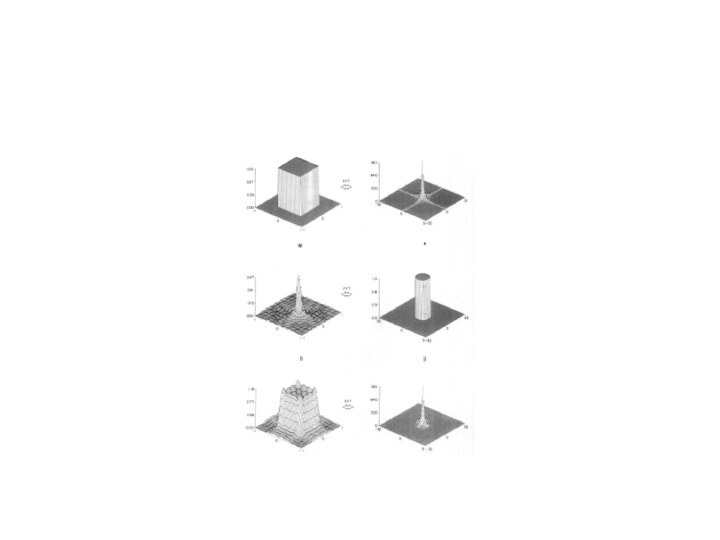
Двумерное преобразование Радона