- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математический словарь
Содержание
- 2. A1 4 По теореме ПифагораВариант 1
- 3. A2 3Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы, значитВариант 1
- 4. A3 1Цифрой десятков числа 123,756 является цифра 2, тогда при округлении до десятковВариант 1
- 5. A4 3Углы при основании равнобедренного треугольника равны, а
- 6. A5 3Вариант 1
- 7. A6 5График симметричен относительно начала координатВариант 1
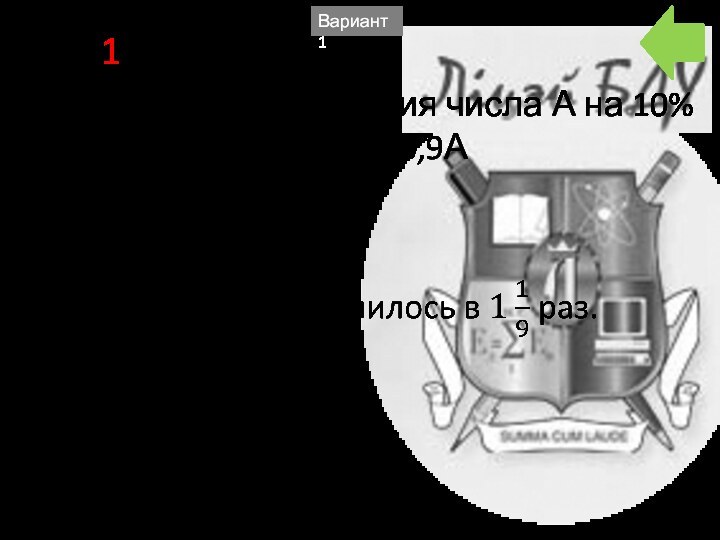
- 8. A7 1В результате уменьшения числа А на 10% получим число, равное 0,9АВариант 1
- 9. A8 5Вариант 1
- 10. A9 1Решим все данные неравенстваВариант 1
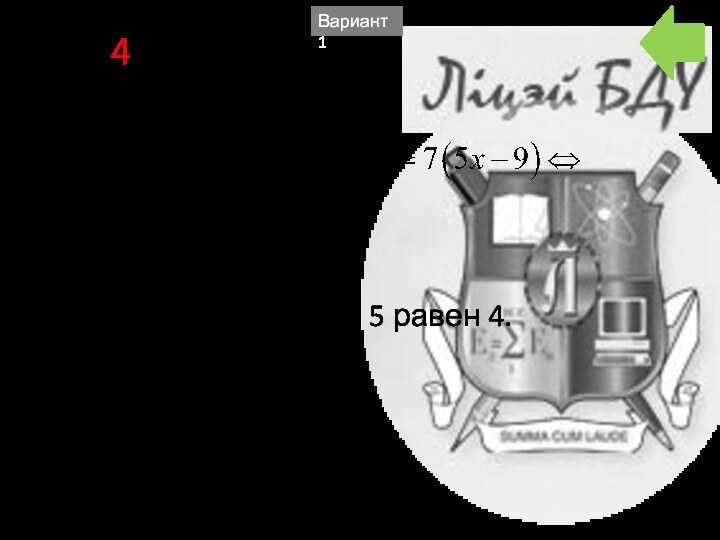
- 11. A10 4Решим уравнениеОстаток от деления 9 на 5 равен 4.Вариант 1
- 12. A11 3Если в трапецию вписана окружность, то
- 13. A12 2Вариант 1
- 14. A13 2Вариант 1
- 15. A14 4Верным является 4 утверждение, т.к.TAD; EDC, а значит прямая TE лежит в плоскости ADC.Вариант 1
- 16. A15 3Пусть было n упаковок по 10
- 17. A16 2В месяц (30 дней) семья из
- 18. A17 3Выделим полный квадратПодставим данное значение aВариант 1
- 19. A18 2Определим разность прогрессииЗапишем формулу n–го члена
- 20. B1 228ABCD – прямоугольная трапеция, площадь которой равнаВариант 1
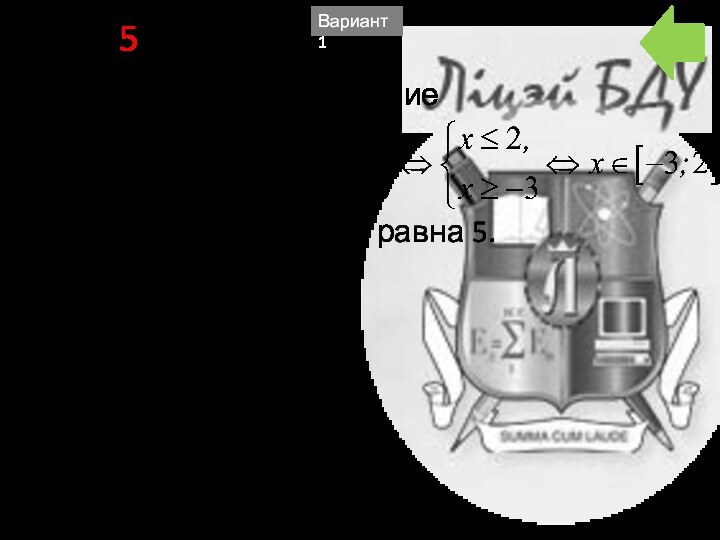
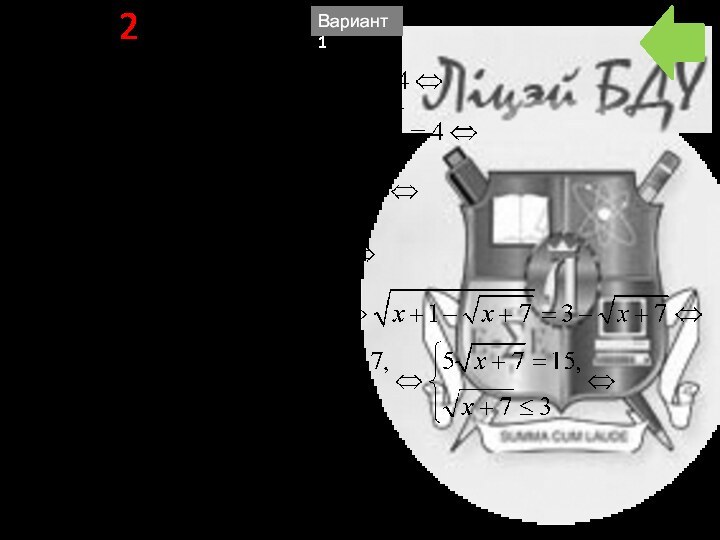
- 21. B2 5Требуется решить уравнениеДлина этого промежутка равна 5.Вариант 1
- 22. B3 -5ТогдаВариант 1
- 23. B4 2Область определения функции задается неравенствомА наибольшее целое число, принадлежащее области определения функции равно 2.Вариант 1
- 24. B5 -5+-+-+Сумма целых решений неравенства равна -3-2=-5Вариант 1
- 25. B6 5Т.к. плоскости α и параллельны,
- 26. B7 -2Вариант 1
- 27. B8 6OE||SD, AEC – сечениеAE=EC, т.к. основанием
- 28. B9 -9Вариант 1
- 29. B10 7Отметим на единичной окружности решения полученной совокупности (синие точки)Вариант 1
- 30. B11 2Вариант 1
- 31. B12 30Скорость плота равна v км/ч.Скорость моторной
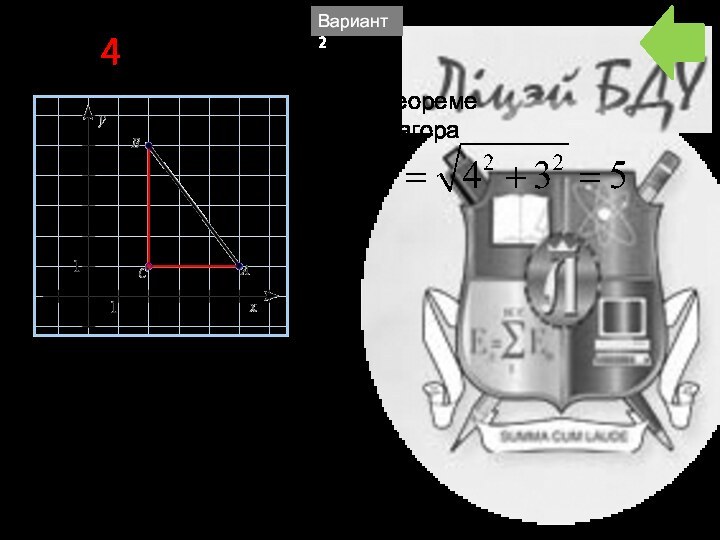
- 32. A1 4 По теореме ПифагораВариант 2
- 33. A2 5Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы, значитВариант 2
- 34. A3 2Цифрой десятков числа 234,678 является цифра 3, тогда при округлении до десятковВариант 2
- 35. A4 5Углы при основании равнобедренного треугольника равны, а
- 36. A5 2Вариант 2
- 37. A6 5График симметричен относительно начала координатВариант 2
- 38. A7 2В результате уменьшения числа А на 30% получим число, равное 0,7АВариант 2
- 39. A8 5Вариант 2
- 40. A9 2Решим все данные неравенстваВариант 2
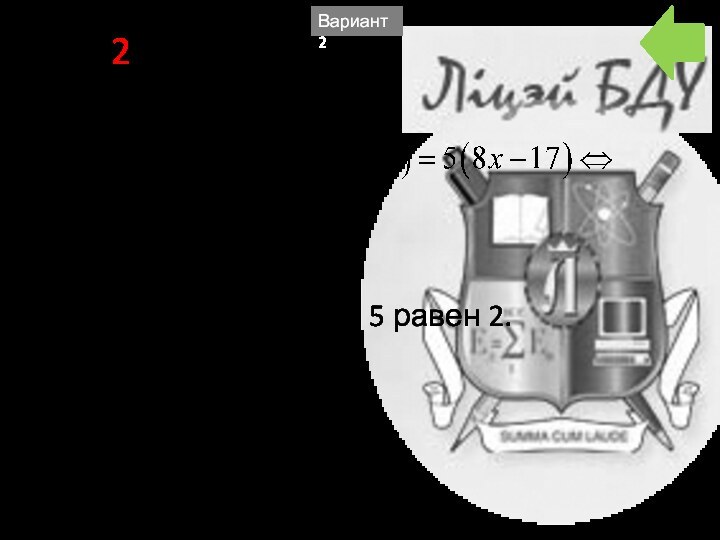
- 41. A10 2Решим уравнениеОстаток от деления 7 на 5 равен 2.Вариант 2
- 42. A11 4Если в трапецию вписана окружность, то
- 43. A12 4Вариант 2
- 44. A13 1Вариант 2
- 45. A14 4Верным является 4 утверждение, т.к.TDС; EBC, а значит прямая TE лежит в плоскости BDC.Вариант 2
- 46. A15 2Пусть было n упаковок по 10
- 47. A16 4В месяц (30 дней) семья из
- 48. A17 3Выделим полный квадратПодставим данное значение aВариант 2
- 49. A18 4Определим разность прогрессииЗапишем формулу n–го члена
- 50. B1 202ABCD – прямоугольная трапеция, площадь которой равнаВариант 2
- 51. B2 8Требуется решить уравнениеДлина этого промежутка равна 8.Вариант 2
- 52. B3 -4ТогдаВариант 2
- 53. B4 3Область определения функции задается неравенствомА наибольшее целое число, принадлежащее области определения функции равно 3.Вариант 2
- 54. B5 -7+-+-+Сумма целых решений неравенства равна -4-3=-7Вариант 2
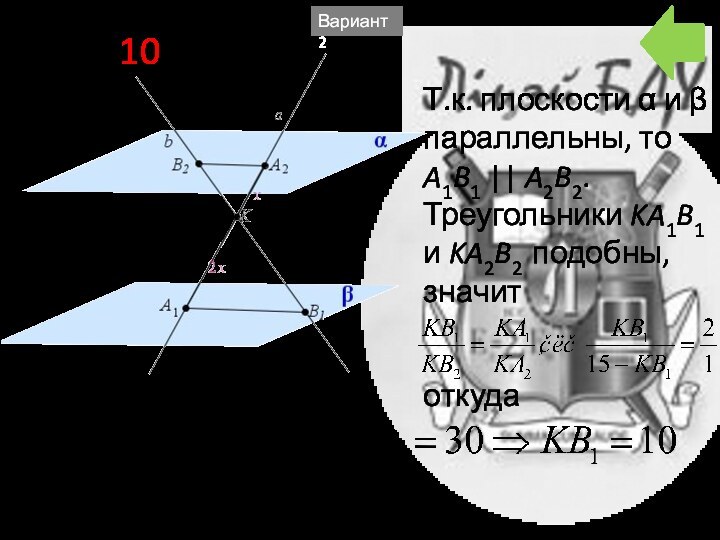
- 55. B6 10Т.к. плоскости α и параллельны,
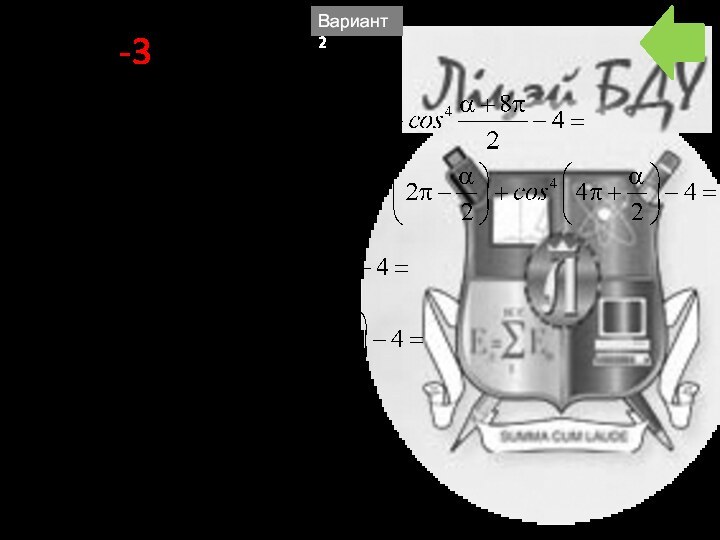
- 56. B7 -3Вариант 2
- 57. B8 3OE||SD, AEC – сечениеAE=EC, т.к. основанием
- 58. B9 -4Вариант 2
- 59. B10 5Отметим на единичной окружности решения полученной совокупности (синие точки)Вариант 2
- 60. B11 4Вариант 2
- 61. Скачать презентацию
- 62. Похожие презентации
A1 4 По теореме ПифагораВариант 1





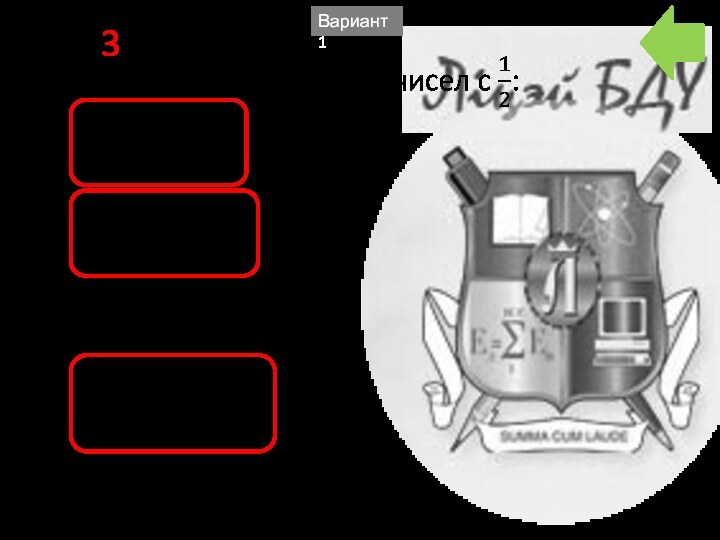















































Слайд 3
A2 3
Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна
половине гипотенузы, значит
Слайд 4
A3 1
Цифрой десятков числа 123,756 является цифра 2, тогда
при округлении до десятков
Вариант 1
Слайд 5
A4 3
Углы при основании равнобедренного треугольника равны, а сумма
всех трёх углов треугольника равна 180, значит, искомый угол
равенВариант 1
Слайд 12
A11 3
Если в трапецию вписана окружность, то BC+AD=AB+CD,
а значит BC+AD=AB+CD=половине периметра трапеции=12.
Средняя линия l равна полусумме
оснований, т.е. 12:2=6Вариант 1
Слайд 15
A14 4
Верным является 4 утверждение, т.к.
TAD; EDC, а
значит прямая TE лежит в плоскости ADC.
Вариант 1
Слайд 16
A15 3
Пусть было n упаковок по 10 книг
и m упаковок по 13 книг. Получим уравнение
Очевидно, что
решениями этого уравнения являются натуральные числа n и m.При умножении на 10 получается число, оканчивающееся нулем, значит m должно быть таким, чтобы 13m оканчивалось 7. Такому условию удовлетворяют числа 9, 19, 29, … Также очевидно, что 13m не может быть больше 237. Получаем, что m=9. Тогда
Суммарное количество упаковок равно 12+9=21.
Вариант 1
Слайд 17
A16 2
В месяц (30 дней) семья из 4
человек может потребить
литров или 16,8м3 воды.
Это количество воды
будет оплачиваться по тарифу 885 р. за кубометр. По условию, семья потребила 20м3 воды. Лишние 3,2 м3 будут оплачиваться по тарифу 2580 р. за кубометр.
Значит за месяц семья заплатит за потреблённые 20 м3 воды
рубля
Вариант 1
Слайд 19
A18 2
Определим разность прогрессии
Запишем формулу n–го члена прогрессии
Требуется
найти номер первого положительного члена прогрессии, т.е.
т.е.
Номер первого
положительного члена прогрессии равен 12.Вариант 1
Слайд 23
B4 2
Область определения функции задается неравенством
А наибольшее целое
число, принадлежащее области определения функции равно 2.
Вариант 1
Слайд 25
B6 5
Т.к. плоскости α и параллельны, то
A1B1 || A2B2.
Треугольники KA1B1 и KA2B2 подобны, значит
откуда
Вариант 1
Слайд 27
B8 6
OE||SD, AEC – сечение
AE=EC, т.к. основанием правильной
4-ой пирамиды является квадрат, значит EO – медиана и
высота треугольника AEC.Вариант 1
Слайд 29
B10 7
Отметим на единичной окружности решения полученной совокупности
(синие точки)
Вариант 1
Слайд 31
B12 30
Скорость плота равна v км/ч.
Скорость моторной лодки
по течению равна v+10 км/ч, против течения равна 10-v
км/ч.Пусть плот до встречи с лодкой проплыл s км. Лодка выехала на 1 ч позже, значит
Плот плавает на 1 час больше, его скорость постоянна, значит он проплывет
И это число должно быть больше 15, т.е.
Лодка догнала катер и вернулась обратно, затратив на весь путь время
Очевидно v+30>0 и v<10, тогда получим v-5>0, т.е. 5 Вариант 1
Слайд 33
A2 5
Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна
половине гипотенузы, значит
Вариант 2
Слайд 34
A3 2
Цифрой десятков числа 234,678 является цифра 3, тогда
при округлении до десятков
Вариант 2
Слайд 35
A4 5
Углы при основании равнобедренного треугольника равны, а сумма
всех трёх углов треугольника равна 180, значит, искомый угол
равенВариант 2
Слайд 42
A11 4
Если в трапецию вписана окружность, то BC+AD=AB+CD,
а значит BC+AD=AB+CD=половине периметра трапеции = 14.
Средняя линия l
равна полусумме оснований, т.е. 14:2=7Вариант 2
Слайд 45
A14 4
Верным является 4 утверждение, т.к.
TDС; EBC, а
значит прямая TE лежит в плоскости BDC.
Вариант 2
Слайд 46
A15 2
Пусть было n упаковок по 10 книг
и m упаковок по 17 книг. Получим уравнение
Очевидно, что
решениями этого уравнения являются натуральные числа n и m.При умножении на 10 получается число, оканчивающееся нулем, значит m должно быть таким, чтобы 17m оканчивалось 2. Такому условию удовлетворяют числа 6, 16, 26, … Также очевидно, что 17m не может быть больше 232. Получаем, что m=6. Тогда
Суммарное количество упаковок равно 13+6=19.
Вариант 2
Слайд 47
A16 4
В месяц (30 дней) семья из 4
человек может потребить
литров или 16,8м3 воды.
Это количество воды
будет оплачиваться по тарифу 885 р. за кубометр. По условию, семья потребила 19м3 воды. Лишние 2,2 м3 будут оплачиваться по тарифу 2580 р. за кубометр.
Значит за месяц семья заплатит за потреблённые 19 м3 воды
рубля
Вариант 2
Слайд 49
A18 4
Определим разность прогрессии
Запишем формулу n–го члена прогрессии
Требуется
найти номер первого положительного члена прогрессии, т.е.
т.е.
Номер первого
положительного члена прогрессии равен 16.Вариант 2
Слайд 53
B4 3
Область определения функции задается неравенством
А наибольшее целое
число, принадлежащее области определения функции равно 3.
Вариант 2
Слайд 55
B6 10
Т.к. плоскости α и параллельны, то
A1B1 || A2B2.
Треугольники KA1B1 и KA2B2 подобны, значит
откуда
Вариант 2
Слайд 57
B8 3
OE||SD, AEC – сечение
AE=EC, т.к. основанием правильной
4-ой пирамиды является квадрат, значит EO – медиана и
высота треугольника AEC.Вариант 2





























