- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математика геометрия
Содержание
- 2. ГЛАВА 1. История математикиГЛАВА 2. МатематикаГЛАВА 3. ГеометрияИ последнее….
- 3. Что такое математика Она изучает числа
- 4. Что такое цифры и числа
- 5. Как появились цифры Но не все делали
- 6. Египетские цифры У каждой цифры
- 7. Римские цифры Древние римляне изобрели свою систему
- 8. 1. Если меньшая цифра стоит слева
- 9. Цифры народов майяи ацтеков У ацтеков было
- 10. Китайские цифры Одна вертикальная палочка обозначала единицу,
- 11. Наша система исчисления Тогда же были позаимствованы
- 12. Неприметный ноль Как бы не так -
- 13. Зачем нужна геометрия Как вы думаете,
- 14. И даже название придумали. Слово "геометрия" состоит
- 15. История геометрии Сначала люди просто наблюдали природу
- 16. Евклидова геометрия Первым математиком-геометром был древнегреческий ученый
- 17. Разделы геометрии Стереометрия - это раздел геометрии,
- 18. Фигура и плоскость Фигура -
- 19. Угол Угол обычно измеряют в градусной мере.
- 20. Многоугольники У каждого многоугольника есть вершина
- 21. Треугольники Треугольник - это многоугольник, у которого
- 22. Если у треугольника равны две боковые
- 23. Круг и окружность Окружность и круг -
- 24. Диаметр - это отрезок, который соединяет две
- 25. Параллели Вы уже знаете, что если
- 26. Умножение - деление Вы знаете, что
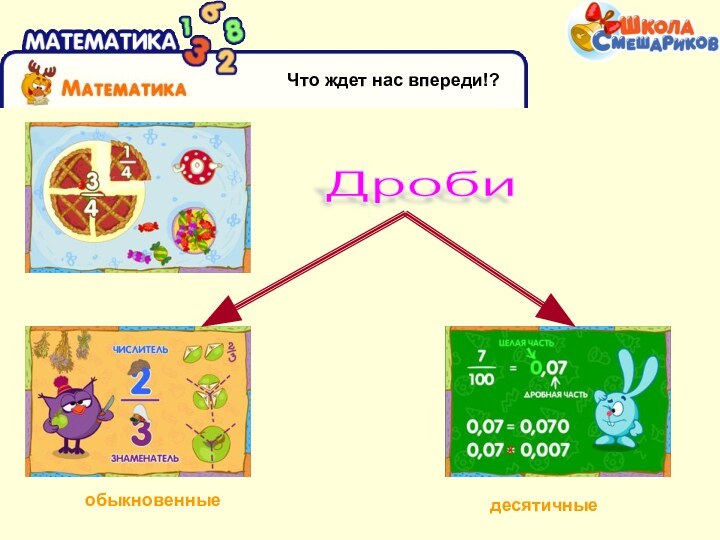
- 27. Что ждет нас впереди!?Дроби обыкновенныедесятичные
- 28. Умножение - деление (+частные случаи - квадрат и куб) степени корни
- 29. прогрессия арифметическая геометрическая
- 31. Скачать презентацию
- 32. Похожие презентации
























Слайд 3
Что такое математика
Она изучает числа и величины,
отношения и характеристики элементов множества, их сходства и отличия,
форму и объем предметов, и способ решения задач с помощью действий!Поэтому, математика и объединяет в себе много различных разделов:
арифметика, геометрия, алгебра, логика и другие, не менее интересные.
Вы знаете, что математика возникла в Древней Греции еще в 6 - 5 веках до нашей эры? У греков эстафету переняли арабы, а уж потом эта новая наука дошла и до европейцев.
Слово "математика" происходит от греческого слова mathema - знание, учение, наука.
Слайд 4
Что такое цифры и числа
А вот древние
люди, для того, чтобы показать какое-то количество чего-либо, использовали
пальцы рук и ног! На протяжении многих веков люди писали числа, считали и вычисляли их в разных формах. Цифры - это одно из древнейших изобретений, которые до нас дошли. Из цифр (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) складываются числа: большие (например, 105) и очень большие (например, 100058945798900014656215)! Мы постоянно используем числа в повседневной жизни. Мы сталкиваемся с ними на каждом шагу (чтобы измерить, купить, продать, позвонить, написать, сосчитать), и настолько свыклись с ними, что даже и не замечаем, насколько они важны.
Слайд 5
Как появились цифры
Но не все делали засечки
на камне или дереве. Вот, например, жрецы Египта писали
на папирусе, а жители Месопотамии - на мягкой глине. Первые цифры представляли собой черточки (для единиц) и разнообразные метки (для десятков и сотен), и у каждой культуры они были свои. Но постепенно знаки становились все сложнее и все понятнее. Первые написанные цифры (о которых нам известно), появились в Египте и Месопотамии около 5000 лет назад. Они представляли собой засечки на дереве или камне.
Слайд 6
Египетские цифры
У каждой цифры от 1 до
10 был свой специальный значок. А еще специальные значки-иероглифы
использовались для обозначения десятков, сотен тысяч, миллионов и даже десятков миллионов! Древняя Египетская цивилизация возникла около 5 тысяч лет назад на севере Африки. Египтяне изобрели папирус, различные системы письма и много сделали для развития геометрии и арифметики.
Писали египтяне иероглифами - то есть, использовали рисунки, чтобы изобразить какой-то объект. И свои цифры они тоже изображали иероглифами.
Слайд 7
Римские цифры
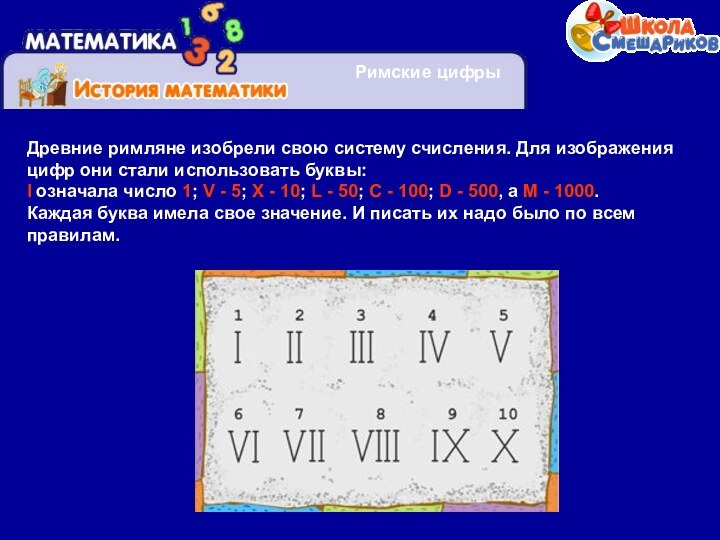
Древние римляне изобрели свою систему счисления. Для
изображения цифр они стали использовать буквы: I означала число
1; V - 5; X - 10; L - 50; C - 100; D - 500, а M - 1000. Каждая буква имела свое значение. И писать их надо было по всем правилам.Слайд 8 1. Если меньшая цифра стоит слева от большей,
то она вычитается, если справа - то прибавляется. Например,
если поставить цифру I (1) перед числом X (10), то получится цифра IX (9), а если ту же самую единичку поставить после X, то получится XI (11)! 2. Все буквы пишутся слева направо, начиная с самого большого значения (например, XIII - это 13, XCIX - это 99, а MCMLXXXVII - это 1987)! 3. Буквы I, X, C и M, могут повторяться подряд три раза (например, III - это 3, а XXX - 30), а вот буквы V, L, D повторять нельзя. 4. Горизонтальная линия над буквой увеличивает значение числа в 1000 раз. Римскими цифрами пользовались очень долго.Сегодня римская система счисления используется там, где это удобно: в литературе (нумерация глав), в оформлении документов и в декоративных целях (на циферблате часов).
Слайд 9
Цифры народов майя
и ацтеков
У ацтеков было четыре
знака. Точка обозначала цифру один, буква h - 20,
перо - 400, а мешок, полный зерна - 8000.Из-за того, что ацтеки использовали так мало знаков, цифры приходилось повторять по много раз, что их ряды были похожи на настоящие иероглифы.
Племена майя использовали всего лишь 3 знака: точку, линию и эллипс. Точка обозначала единицу, а линия - цифру пять. Составляя различные комбинации из точек и линий, можно было написать любое число до 19! А эллипс увеличивал написанное в 20 раз.
Слайд 10
Китайские цифры
Одна вертикальная палочка обозначала единицу, 5
палочек - пятерку, У цифр от 6 до 9
сверху еще добавлялась горизонтальная палочка - все было легко и понятно. Эта система отличалась тем, что была "позиционной", то есть число зависело от того, какое место занимала цифра в ряду. Если, например, хотели написать 1953, то просто подряд ставили цифры 1, 9, 5 и 3.В конце 19 века крестьяне-земледельцы нашли много черепашьих панцирей и костей животных. Они были исписаны знаками древней китайской системы исчисления.
Оказывается, древние китайцы придумали эту систему очень давно - между 1500 и 1200 годами до нашей эры. Палочками из слоновой кости или бамбука они обозначали цифры от одного до девяти.
Слайд 11
Наша система исчисления
Тогда же были позаимствованы и
цифры. Впервые индийскую систему записи использовал арабский учёный Мухаммед
ибн Муса аль-Хорезми. Он написал Китаб аль-Джебр ва-ль-Мукабаля, книгу, от названия которой произошёл термин "алгебра". Современные цифры не сильно похожи на индийские, потому что арабы их видоизменили и приспособили к своему письму. Да и со старыми арабскими цифрами у них немного общего. Может быть, потому что для экономии места арабские цифры изображались боком.Цифры, которыми мы с вами привыкли пользоваться, называются арабскими. Они имеют арабское происхождение, но на самом деле, они были заимствованы арабами у индийцев.
Самый расцвет науки в мусульманском мире произошел между 8 и 13 веками. Как раз тогда мусульмане тесно общались и сотрудничали и с азиатской, и с европейской культурами, и, конечно, брали у этих культур все самое лучшее.
Слайд 12
Неприметный ноль
Как бы не так - без
ноля никак не прожить!
Вот, например, припишите к любому
числу обычный нолик, и значение числа возрастет в 10 раз. Или поделите полученное число на ноль, и получится бесконечность. А при умножении все наоборот! Самое огромное число, прикоснувшись к нолику, тут же становится нолем. Фантастика!
Знаете, какая цифра в математике - самая удивительная?
Конечно же, ноль!
Поначалу ноль никому не был нужен. Давным-давно эту цифру боялись, ненавидели, и даже запрещали! Все думали, что, раз за этим значком не скрывается никакой реальной величины, то он не пригодится.
Слайд 13
Зачем нужна геометрия
Как вы думаете, зачем нам
нужна геометрия? А вы посмотрите вокруг - геометрия повсюду!
Высотные здания, космические станции, автомобили, бытовая техника, дорожные развязки и городские парки - это все геометрия. Куда же без нее?Геометрия - это раздел математики, которая изучает формы предметов и их пространственные отношения.
Родоначальниками геометрии были древние греки. Они были настоящими учеными, потому что, переняв у египтян ремесло измерения земли и объемов тел, смогли превратить его в науку. Самая главная книга "Начало" была написана в 3 веке до нашей эры греческим математиком Евклидом.
Слайд 14 И даже название придумали. Слово "геометрия" состоит из
двух древнегреческих слов: geo - "земля" и metreo -
"измеряю", "землемерие".Это из-за того, что главной задачей геометрии в древности было измерение земельных участков.
Геометрия - одна из самых древних математических наук. Родоначальниками геометрии считаются древние греки. Они были настоящими учеными, потому что, переняв у египтян ремесло измерения земли и объемов тел, смогли превратить его в науку
Слайд 15
История геометрии
Сначала люди просто наблюдали природу и
учились измерять. Они измеряли длины дорог, величины углов и
площади земельных участков. Потом придумали способы и формулы, с помощью которых можно было узнать те вещи, которые так просто (при привычном измерении) узнать было невозможно.И уж только потом ученые поняли, что правильность формул и наблюдений нужно доказывать - так появились доказательства. Это было очень давно - в первом тысячелетии до нашей эры!
Слайд 16
Евклидова геометрия
Первым математиком-геометром был древнегреческий ученый Евклид.
Еще в III веке до нашей эры он написал
книгу под названием "Начала".Геометрию греков сейчас так и называют - евклидова или элементарная. Евклидова геометрия занималась изучением самых простых форм: прямых, плоскостей, отрезков, многоугольников, шаров, цилиндров, призм и многого другого.
Именно эту геометрию мы с вами изучаем в своих школах.
Слайд 17
Разделы геометрии
Стереометрия - это раздел геометрии, который
изучает фигуры в пространстве.
Геометрия делится на два раздела: планиметрия
и стереометрияИменно с планиметрии начинается изучение геометрии в школах. Планиметрия происходит от латинского "planum"-плоскость, и греческого "metreo" - измеряю.
Этот раздел геометрии изучает двумерные фигуры, то есть фигуры, которые располагаются на плоскости: точка, прямая, плоскость и расстояние.
Слайд 18
Фигура и плоскость
Фигура - латинское слово, означающее
образ, вид, начертание. Этот термин появился в 12 веке.
А до 12 века чаще говорили другое латинское слово - "форма".Оно тоже означало наружный вид и внешнее очертание предмета.
В наше время геометрическая фигура - это часть плоскости, которая ограничена со всех сторон линиями.
Плоскость - это одно из самых главных понятий в геометрии. Это абсолютно ровная бесконечная поверхность. Представьте себе ровный бесконечный стол или лист бумаги. Представили? Вот вам и плоскость!
На плоскости располагаются разные фигуры.
Слайд 19
Угол
Угол обычно измеряют в градусной мере. Полный
круг равен 360о. Это означает, что он разделен на
360 одинаковых частей. Значение 90о считается самым основным для определения вида угла. Углы же разные бывают: прямые, острые и тупые. Прямой угол равен 90о. Если угол меньше 90о, то его называют острым. А если он больше 90о, то - тупым. Все просто!А часть плоскости между двумя пересекающимися линиями называют углом.
Две прямые, расположенные на одной плоскости, могут пересекаться.
Точка, в которой эти прямые пересекаются, называется точкой пересечения
Угол
Слайд 20
Многоугольники
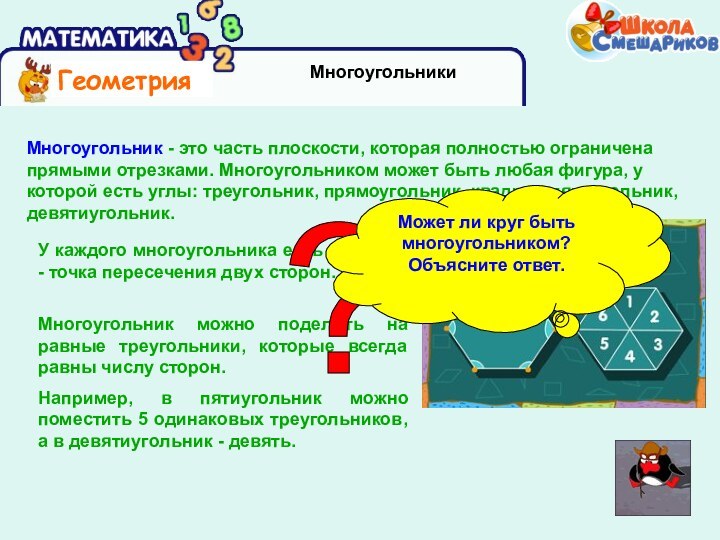
У каждого многоугольника есть вершина - точка
пересечения двух сторон.
Многоугольник можно поделить на равные треугольники,
которые всегда равны числу сторон. Например, в пятиугольник можно поместить 5 одинаковых треугольников, а в девятиугольник - девять.
Многоугольник - это часть плоскости, которая полностью ограничена прямыми отрезками. Многоугольником может быть любая фигура, у которой есть углы: треугольник, прямоугольник, квадрат, пятиугольник, девятиугольник.
?
Может ли круг быть многоугольником? Объясните ответ.
Слайд 21
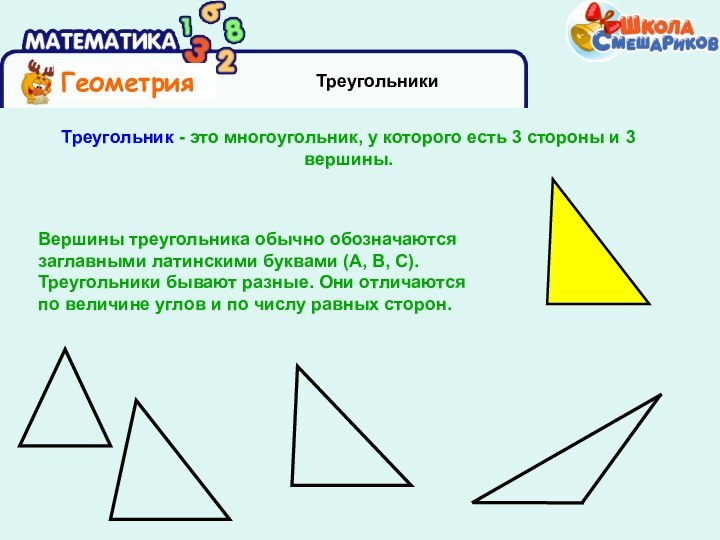
Треугольники
Треугольник - это многоугольник, у которого есть
3 стороны и 3 вершины.
Вершины треугольника обычно обозначаются заглавными
латинскими буквами (A, B, C). Треугольники бывают разные. Они отличаются по величине углов и по числу равных сторон.
Слайд 22 Если у треугольника равны две боковые стороны и
два угла, он называется равнобедренным.
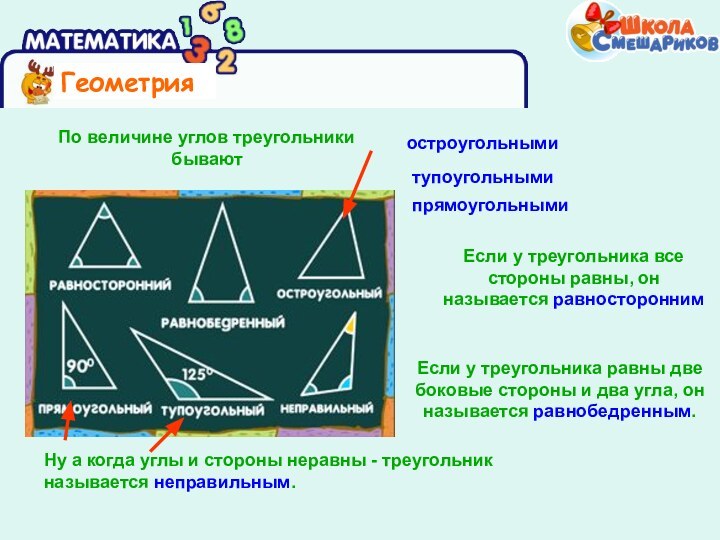
По величине углов треугольники
бываютостроугольными
тупоугольными
прямоугольными
Если у треугольника все стороны равны, он называется равносторонним
Ну а когда углы и стороны неравны - треугольник называется неправильным.
Слайд 23
Круг и окружность
Окружность и круг - не
одно и то же. Окружность - это замкнутая прямая
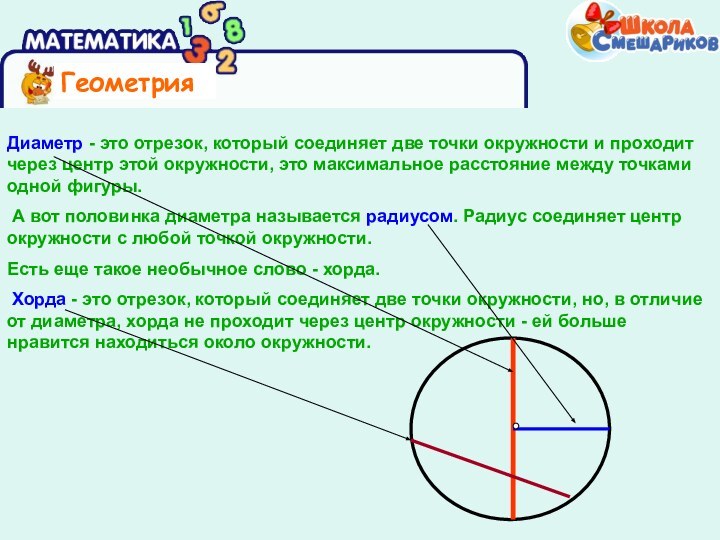
линия, все точки которой расположены на одинаковом расстоянии от одной внутренней точки, которая называется центром. А круг - это часть плоскости, ограниченная окружностью.Слайд 24 Диаметр - это отрезок, который соединяет две точки
окружности и проходит через центр этой окружности, это максимальное
расстояние между точками одной фигуры.А вот половинка диаметра называется радиусом. Радиус соединяет центр окружности с любой точкой окружности.
Есть еще такое необычное слово - хорда.
Хорда - это отрезок, который соединяет две точки окружности, но, в отличие от диаметра, хорда не проходит через центр окружности - ей больше нравится находиться около окружности.
Слайд 25
Параллели
Вы уже знаете, что если две прямые
линии пересекаются в какой-то точке, то они образуют угол.
А вот если они не пересекаются, то они называются параллельными прямыми. Если две прямые параллельны третьей прямой, значит, между собой эти две прямые тоже параллельны.
Слайд 26
Умножение - деление
Вы знаете, что такое умножение
и деление?
Да знаем, конечно, - мы же в
Школу ходим! В пятый класс!!!Но все равно, давайте, я вам напомню! И умножение, и деление - это математические действия. С помощью умножения определенное число складывается само с собой несколько раз.
Сколько раз? А столько, сколько указывает другое число! Например, 5*3 означает, что 3 числа 5 будут сложены друг с другом: 5+5+5=15.
А при делении, все происходит наоборот! Деление разделяет число на несколько равных частей.
Например, 15:3=5, то есть 1/3 от 15 - это 5. А теперь давайте проверим - сложим друг с другом три пятерки: 5+5+5=15!