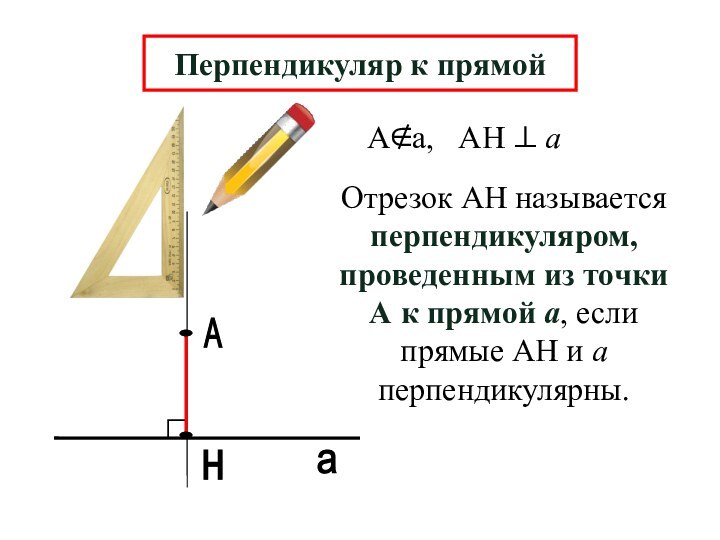
точки А к прямой а, если прямые АН и
а перпендикулярны.А∉а, АН ⊥ а
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






А∉а, АН ⊥ а