- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод искусственного базиса
Содержание
- 2. Вспомогательная задача к ЗЛП (1): (2)Вектор составлен
- 3. Искусственные переменные не несут никакого экономического смысла.
- 4. Теорема. (О существовании плана ЗЛП).
- 5. П р и м е р: Рассмотрим ЗЛП:Приведем данную ЗЛП к каноническому виду:
- 6. Единичного базиса
- 8. Решив данную вспомогательную задачу симплекс-методом, мы найдем
- 9. Признак неограниченности целевой функции ЗЛП в канонической
- 10. В уравнении
- 11. Теорема. О неразрешимости ЗЛП.Если для некоторого БДП
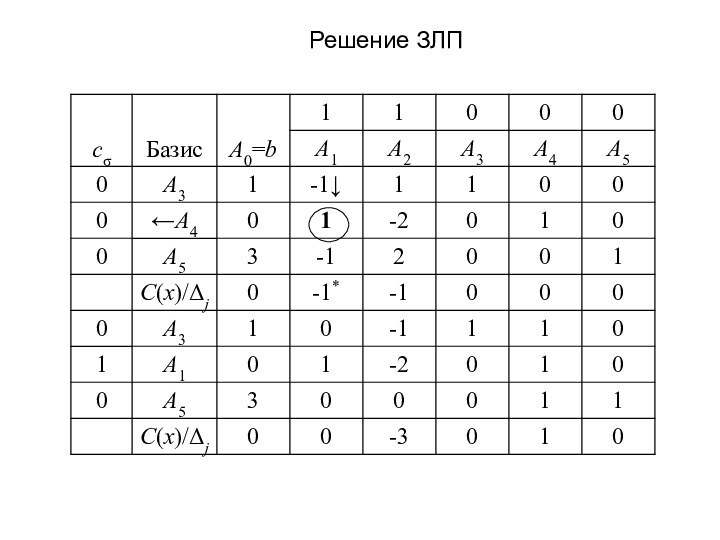
- 12. Пример:Единичный базис состоит из векторов А3, А4,
- 13. Решение ЗЛП
- 14. Скачать презентацию
- 15. Похожие презентации
Вспомогательная задача к ЗЛП (1): (2)Вектор составлен из естественных переменных ЗЛП (1.) и искусственных переменных, введенных в ЗЛП (2):






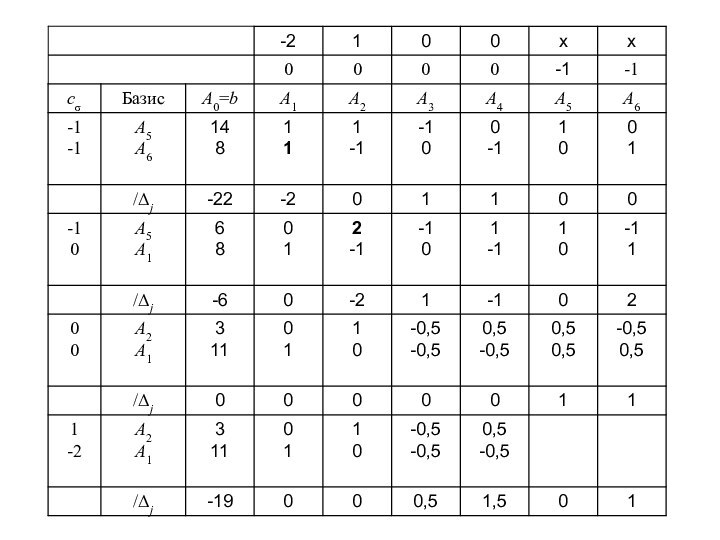






Слайд 3 Искусственные переменные не несут никакого экономического смысла. Они
необходимы только для поиска начального БДП.
Единичные векторы An+1,
An+2, …, An+m образуют искусственный базис системы ограничений ЗЛП (2). Они представляют собой единичную матрицу размера m × m. В ЗЛП (2) мы имеем начальный БДП, в котором первые n координат равны нулю.
Пусть множество допустимых планов задачи (1) - D1, а множество допустимых планов задачи (2) - D2.
Слайд 4
Теорема. (О существовании плана ЗЛП).
Пусть
оптимальный план ЗЛП (2), тогда:
Если , то план является планом задачи (1), т.е. ∈D1.
Если , то ЗЛП (1) не имеет допустимых планов, т.е. D1 есть пустое множество (D1 = ∅).
Замечание. Вспомогательная задача (2) всегда имеет оптимальный план.
Слайд 6 Единичного базиса нет,
поэтому построим вспомогательную задачу, предварительно введя две искусственные переменные
х5 ≥ 0 и х6 ≥ 0.Слайд 8 Решив данную вспомогательную задачу симплекс-методом, мы найдем ее
оптимальный план и значение целевой функции на этом плане:
Оптимальный
план вспомогательной задачи есть начальный БДП основной задачи. После чего необходимо приступить к ее решению также симплекс-методом. Оптимальный план основной задачи:х* = (11; 3; 0; 0); С1(х*) = – 19; С(х*) = 19
Слайд 9
Признак неограниченности целевой функции
ЗЛП в канонической форме:
Пусть
х0 = (х10, х20,…, хn0) - БДП задачи (1)
Ax0 = b эквивалентно (1)
σ - носитель плана, следовательно - ,
или в матричной форме записи:
(2)
Слайд 10 В уравнении (2)
хσ0 представляет часть исходного вектора х0 , из которого
удалены нулевые (свободные) компоненты. Для плана х0 можно построить симплекс-таблицу, причем предположим, что среди двойственных оценок имеются отрицательные , т.е. план не оптимальный.
Слайд 11
Теорема. О неразрешимости ЗЛП.
Если для некоторого БДП х0
существует Δk < 0 и все элементы k-го вектор-столбца
меньше или равны нулю, т.е. , i∈σ, то ЗЛП неразрешима. Другими словами, в данной ситуации целевая функция не ограничена на допустимом множестве, т. е. С(х) → + ∞.