- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методика исследования функций и построение их графиков
Содержание
- 2. Структура работыТеоретическая частьТехнологическая частьГотфрид Вильгельм Лейбниц
- 3. Теоретическая частьВозникновение развития понятия функции Определение функции
- 4. Термин «функция» принадлежит Лейбницу и происходит от
- 5. Функции непрерывные и разрывные
- 6. С помощью теоремы Больцано можно решить, например,
- 7. Функции вида Многочлены – основные средства
- 8. Исследование функции и построение графикаОбласть определения и
- 9. Исследование функций и построение их графиков с
- 10. Технологическая частьРазличные подходы к определению понятия функция
- 11. Различные подходы к определению понятия функция •
- 12. Основные подходы к введению понятия «функция»
- 13. Методика введения понятия функции в учебниках различных
- 14. Особенности изучения отдельных классов функцийа)прямой и обратной
- 15. Единый государственный экзамен преподносит нам немало сюрпризов,
- 16. Тип урока: семинарТема урока «Основные
- 17. Тип урока: урок повторения
- 18. Тематическое планирование факультативного курса«Исследование функций и построение
- 19. Основные способы преобразования
- 20. Основные способы преобразования графиковСимметрия относительно осей координат относительно оси ??относительно оси ??
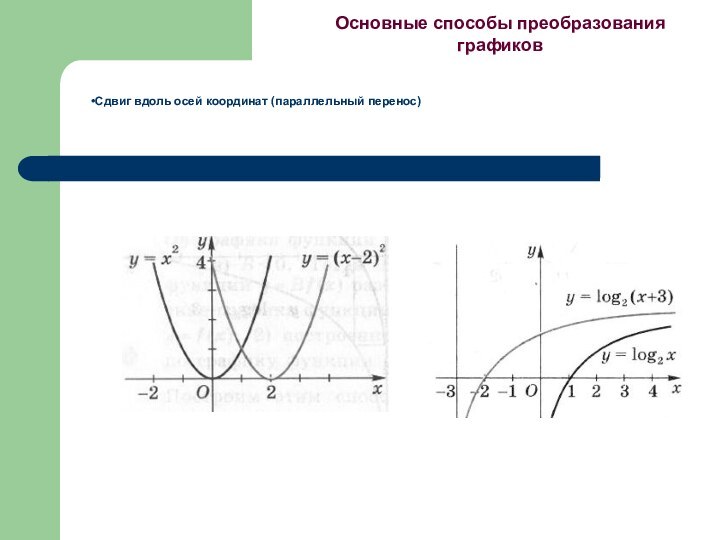
- 21. Сдвиг вдоль осей координат (параллельный перенос)Основные способы преобразования графиков
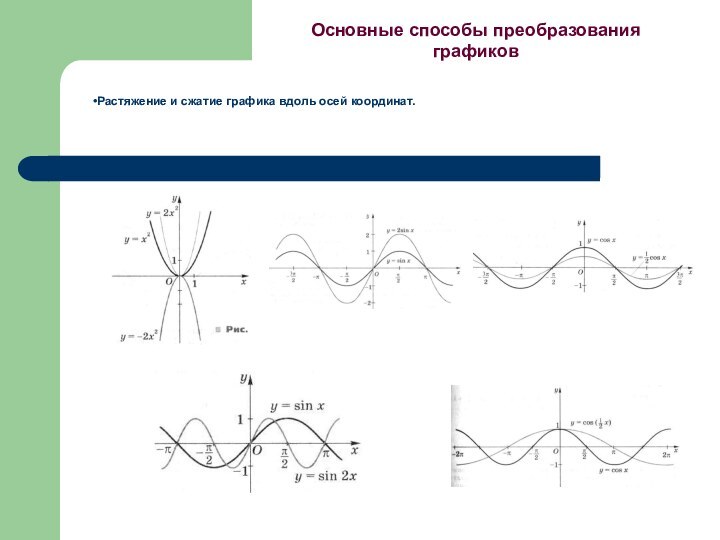
- 22. Растяжение и сжатие графика вдоль осей координат.Основные способы преобразования графиков
- 23. Графики функций, связанных с модулем.Основные способы преобразования графиков
- 24. Скачать презентацию
- 25. Похожие презентации



















Слайд 3
Теоретическая часть
Возникновение развития понятия функции
Определение функции
Элементарные
функции и их свойства
Способы задания функции
Функции непрерывные
и разрывные Исследование функций и построение их графика
Готфрид Вильгельм Лейбниц
Слайд 4 Термин «функция» принадлежит Лейбницу и происходит от латинского
слова functio,что означает «выполнение», «осуществление».
Способы задания функции
степенные, показательные,
логарифмические,
тригонометрические,
обратные тригонометрические,
гиперболические,
обратные гиперболические,
Табличный
Аналитический
Графический
Словесный
а также функции, получаемые из них с помощью четырех арифметических действий (сложения, вычитании, умножения и деления) и с помощью операции взятия функции от функции.
элементарные функции:
Слайд 5
Функции непрерывные и разрывные
Рисунок 1
Рисунок 2
одним росчерком карандаша без
отрыва от бумагииз двух непрерывных фрагментов
график нельзя нарисовать без отрыва карандаша от бумаги
Непрерывные функции образуют основной класс функций
«чрезвычайно разрывные» функции
- функция Дирихле
Владимир Игоревич Арнольд
Лежен Дирихле
Среди разнообразных функций одной переменной выделяются те, график которых можно нарисовать одним росчерком карандаша без отрыва от бумаги. Такова функция, представленная на рисунке 1.
Слайд 6 С помощью теоремы Больцано можно решить, например, такую
известную занимательную задачу.
Некий путешественник в 9 утра начал
подъем в гору и ровно в 6 вечера достиг вершины. Заночевав на вершине, на следующий день он ровно в 9 утра начал спуск по той же тропе и ровно в 6 вечера достиг исходного пункта у подножия. Верно ли, что в каком-то месте на тропе путешественник находился в одно и то же время первого и второго дня путешествия?Бернард Больцано
Иллюстрация к доказательству теоремы о непрерывной функции
Слайд 7
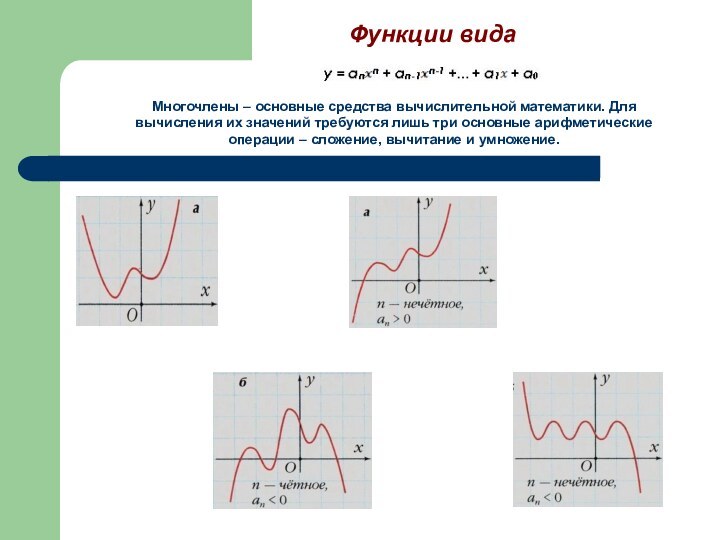
Функции вида
Многочлены – основные средства вычислительной
математики. Для вычисления их значений требуются лишь три основные
арифметические операции – сложение, вычитание и умножение.
Слайд 8
Исследование функции и построение графика
Область определения и область
изменения функции
Ограниченность функции
Четность, нечетность, периодичность функций
Промежутки возрастания, убывания, знакопостоянства
и нули функциисхематический
график
Наглядность графика является вспомогательным средством исследования функции. График только иллюстрирует свойства функции, но не доказывает их.
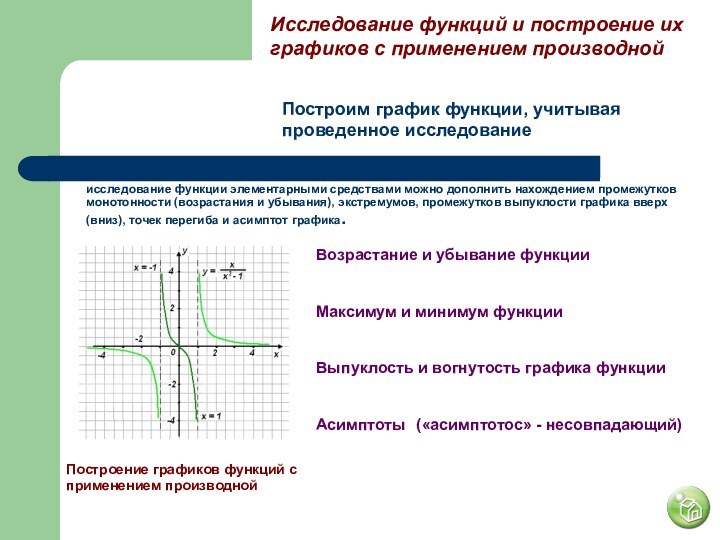
Слайд 9 Исследование функций и построение их графиков с применением
производной
Возрастание и убывание функции
Максимум и минимум функции
Выпуклость и вогнутость
графика функцииАсимптоты
Построение графиков функций с применением производной
Построим график функции, учитывая проведенное исследование
(«асимптотос» - несовпадающий)
исследование функции элементарными средствами можно дополнить нахождением промежутков монотонности (возрастания и убывания), экстремумов, промежутков выпуклости графика вверх (вниз), точек перегиба и асимптот графика.
Слайд 10
Технологическая часть
Различные подходы к определению понятия функция
Методика введения понятия функции в
учебниках различных авторовМетодические особенности изучения отдельных классов функций
Разработка уроков
Тематическое планирование факультативного курса
«Исследование функций и построение их графиков»
Слайд 11
Различные подходы к определению понятия функция
• цель
и значение изучения понятия функции учащимися;
• подходы к определению
функции;• вопрос функциональной пропедевтики;
• место и объем функционального материала в курсе школьной математики.
линейные функции и их графики;
квадратичные функции;
функции обратной пропорциональности и дробно-линейные функции;
тригонометрические функции;
показательные и логарифмические функции.
три основные направления введения понятия «функция»:
• упорядочение имеющихся представлений о функции, развертывание системы понятий, характерных для функциональной линии (способы задания и общие свойства функций, графическое истолкование области определения, области значений, возрастания и т. д. на основе метода координат);
• глубокое изучение отдельных функций и их классов;
• расширение области приложений алгебры за счет включения в нее идеи функции и разветвленной системы действий с функцией.
Хинчин
Александр Яковлевич
классы функций:
понятие функциональной зависимости должно стать не только одним из важнейших понятий школьного курса математики, но тем основным стержнем, проходящим от элементарной арифметики до высших разделов алгебры, геометрии, тригонометрии, вокруг которых группируется все математическое представление.
Слайд 13
Методика введения понятия функции в учебниках различных авторов
Учитывая
восприимчивость к новым математическим понятиям, основные свойства функций перенесли
на старшую ступень авторы учебников под редакцией А.Г.Мордковича и С.М.Никольского.Приоритетной линией комплекта А.Г. Мордковича является функционально-графическая линия:
Функциональная линия в комплекте учебников под редакцией С.М.Никольского занимает ведущее место среди тем учебного курса.
овладеть методами исследования функций и построения их графиков;
усвоить понятие предела функции и непрерывности функции в точке и на интервале;
усвоить понятие функции, обратной данной, и научить находить функцию, обратную данной;
научить находить производную любой элементарной функции;
научить применять производную при исследовании функций и решении практических задач.
Слайд 14
Особенности изучения отдельных классов функций
а)прямой и обратной пропорциональной
зависимости:
• опора на знания о пропорции и пропорциональной
зависимости величин.• индуктивный подход к введению понятия.
• использование приема «загущения» точек при построении графика.
б)линейной функции:
а) нанесение нескольких точек;
б) наблюдение — все построенные точки расположены на одной прямой; проведение этой прямой;
в) проверка: берем произвольное значение аргумента и вычисляем по нему значение функции; наносим точку на координатную плоскость — она принадлежит построенной прямой. Отсюда делается вывод о графике данной линейной функции.
построение графика методом «загущения» точек ;
оценочное исследование функции;
характеристическим точкам;
с помощью преобразования графика простейшей функции ? = ?².
в)степенной, показательной и логарифмической функций:
Строится по аналогичным схемам. Главной особенностью является наличие больших ограничений на параметры, ограничение области определения функции.
г)тригонометрических функций
нахождение значений всех тригонометрических функций в «главных» точках.
Сначала по точкам строится график, а затем с помощью графической интерпретации исследуются все свойства функции.
д)квадратичной функции:
Слайд 15 Единый государственный экзамен преподносит нам немало сюрпризов, где
помимо нахождения самого множества значений функции, его подмножеств, наибольшего
или наименьшего значения функции и т. д., требуется применить его к решению уравнений либо неравенств. Часто, решая задачи, мы сталкивается с необходимостью отыскания области значений той или иной функции.Тип урока: лекция Мастер - класс
Тема урока «Множество значений функции: нестандартные задачи»
1.Найдите множество значений функции y = sin ? + cos ?.
(способом введения вспомогательного угла)
.
2.Найдите множество значений функции ? =
Выясним, при каких значениях, а уравнение
=
имеет решение
Уравнение равносильно системе:
.
3.Числа ? и ? удовлетворяют равенству
Найдите все значения, которые может принимать сумма ?² + y².
Найдем все значения
:
, :
которых имеет решение система уравнений при
Цель нашего урока – представить различные методы нахождения множества значений функции.
Слайд 16
Тип урока: семинар
Тема урока «Основные свойства
функции»
Цель урока:
1. Повторить основные
свойства функции.2. Рассмотреть дробно-линейную и дробно-рациональную функции, мало изучаемые
в школьной программе.
3. Рассмотреть примеры функций, содержащих модуль.
4. Прививать интерес к построению графиков функций повышенной сложности.
Задачи урока:
1. Углубление и систематизация знаний по теме «Основные свойства функции».
2. Подготовка учащихся к вступительным экзаменам в технические ВУЗы.
3. Воспитание учащихся целеустремленности, умение доводить все начатое до логического конца, культуры построения графиков функций.
Сообщения по заданным темам.
1) Функции в природе и технике
2) Дробно-линейная функция и ее график
3) Графики функций, содержащих модуль
4) Дробно-рациональная функция
5) Тригонометрические функции
в)? =
Рис.19 Рис.20 Рис.21 Рис.22
.
Построить графики:
а) ? =
?
в)? =
г) у = 2
Слайд 17 Тип урока: урок повторения
Тема урока «Свойства функции и их графики»
Уроки повторения имеют своей целью не только восстановление в памяти
учащихся основного материала, но и обобщение, уточнение и
систематизацию их знаний по алгебре и началам анализа за курс средней школы элементом на уроке повторения должна быть самостоятельная работа учащихся.
Цель урока:
обобщить теоретические знания по теме, рассмотреть решения задач, связанных с этой темой, базового и повышенного уровня сложности;
организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных у них знаний.
Слайд 18
Тематическое планирование факультативного курса
«Исследование функций и построение их
графиков»
• Тема 1. «Понятия функции и графика. Задание
функций».• Тема 2. «Классы функций».
• Тема 3. «Разрывные функции и их графики».
• Тема 4. «Кусочно-линейные функции и модули».
• Тема 5. «Графики многочленов».
• Тема 6. «Графики дробно-рациональных функций».
• Тема 7. «Тригонометрические функции».
• Тема 8. «Построение графиков сложных функций».
• Тема 9. «Использование графиков функций для решения различных задач».
• Тема 10. «Итоговая диагностика».
Слайд 19 Основные способы преобразования
графиков
Симметрия относительно осей координат
Сдвиг вдоль осей координат (параллельный перенос)
Растяжение и сжатие графика вдоль осей координат.
Построение графика функции ? = ??(?(?‒?))+? по графику функции ?=?(?).
Графики функций, связанных с модулем.
график функции, содержащий модуль