- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы аппроксимации, интерполяции, экстраполяции в математическом пакете Mathcad. (Лекция 4)
Содержание
- 2. Аппроксимация Замена одних математических объектов другими, в
- 3. Аппроксимация функций заключается в приближенной замене заданной
- 4. На отрезке [a, b] заданы n + 1 точки
- 5. В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь решений.
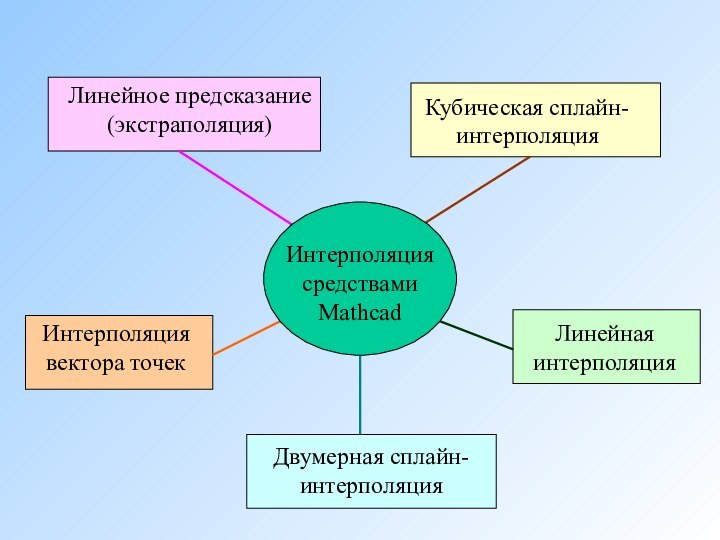
- 6. Виды интерполяции
- 7. Интерполяция средствами Mathcad
- 8. Является простейшим и часто используемым видом локальной
- 9. Линейная интерполяция в MathCADПри линейной интерполяции MathCAD
- 10. Линейная интерполяция в MathCAD
- 11. Наиболее широкое практическое применение, в силу их
- 12. В общем случае для функции y =
- 14. Кубическая сплайн-интерполяция в MathCADПроводит кривую через набор
- 15. Построения кубического сплайна через набор точек:Создать векторы
- 16. Кубическая сплайн-интерполяция в MathCAD
- 17. Можно использовать оператор векторизации, чтобы вычислить сразу
- 18. Функция predict В Mathcad позволяет оценить значения
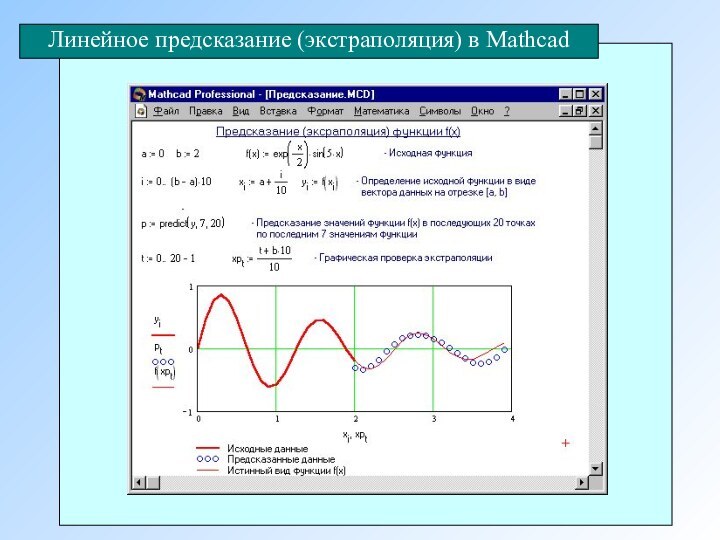
- 19. Линейное предсказание (экстраполяция) в Mathcad
- 20. Двумерная сплайн-интерполяцияИспользуют для повышения качества построения 3D-графиков.
- 21. Построения двумерной сплайн-интерполяции Первый шаг точно такой
- 22. Скачать презентацию
- 23. Похожие презентации

![Методы аппроксимации, интерполяции, экстраполяции в математическом пакете Mathcad. (Лекция 4) На отрезке [a, b] заданы n + 1 точки xi = х0, х1, . . ., хn, которые называются узлами интерполяции,](/img/tmb/15/1481242/cc101818d9af2a4ad5ab37068b48a924-720x.jpg)












Слайд 3
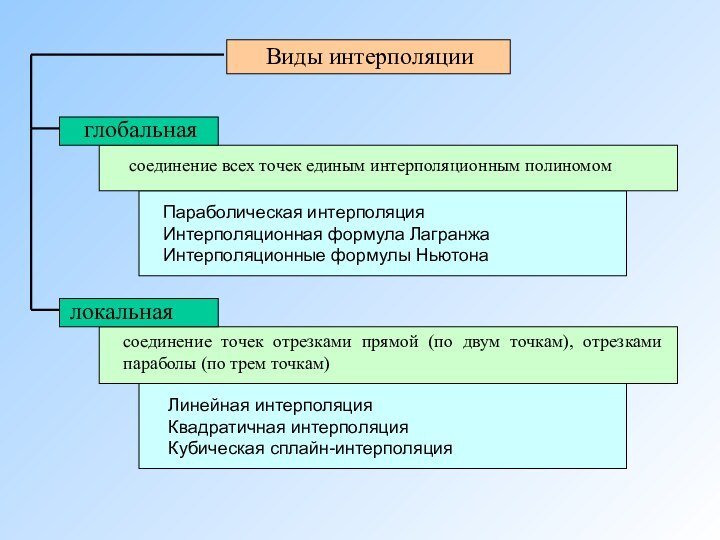
Аппроксимация функций заключается в приближенной замене заданной функции
f(x) некоторой функцией φ (x) так, чтобы отклонение функции
φ (x) от f(x) в заданной области было наименьшим. Функция φ (х) при этом называется аппроксимирующей.
Слайд 4
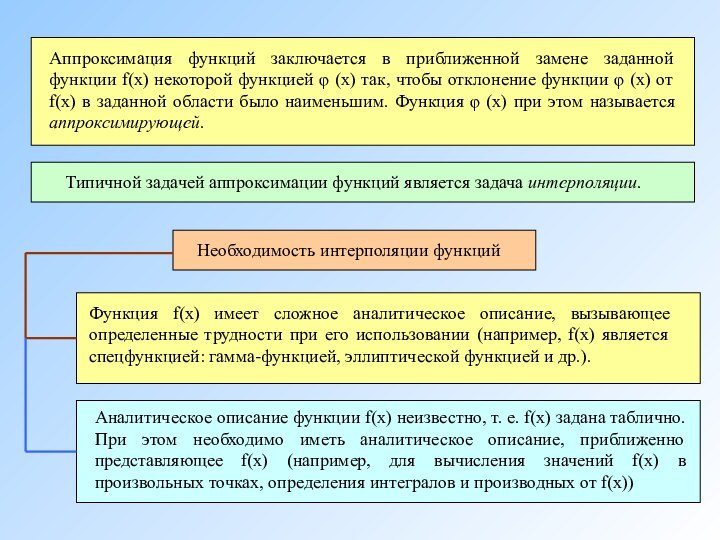
На отрезке [a, b] заданы n + 1 точки xi = х0, х1, . . ., хn,
которые называются узлами интерполяции, и значения некоторой функции f(x)
в этих точкахПростейшая задача интерполяции
f(x0) = y0, f(x1) = y1, . . ., f(xn) = yn.
Требуется построить функцию F (х) (интерполяционная функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т. е. такую, что
F(x0) = y0, F(x1) = y1, . . ., F(xn) = yn.
Геометрически это означает, что нужно найти кривую y = F (х) некоторого определенного типа, проходящую через заданную систему точек M(xi, yi) (i = 0, 1, ..., n)
Слайд 5
В такой общей постановке задача может иметь бесконечное
множество решений или совсем не иметь решений.
Слайд 8
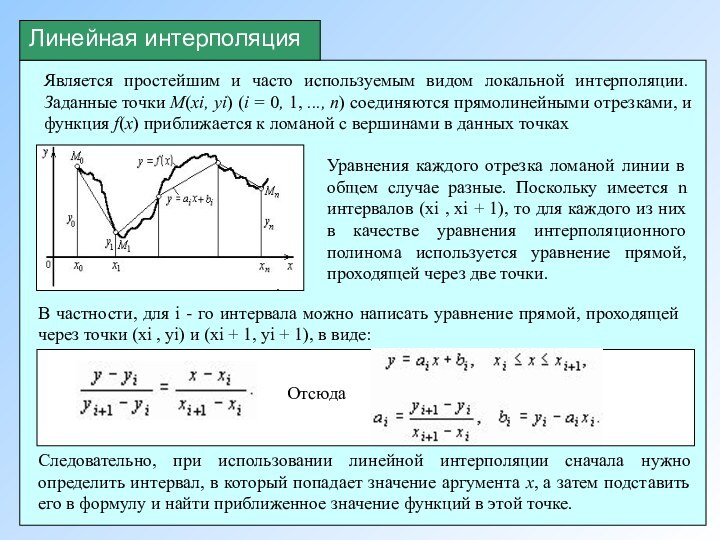
Является простейшим и часто используемым видом локальной интерполяции.
Заданные точки М(xi, yi) (i = 0, 1, ...,
n) соединяются прямолинейными отрезками, и функция f(x) приближается к ломаной с вершинами в данных точкахУравнения каждого отрезка ломаной линии в общем случае разные. Поскольку имеется n интервалов (xi , xi + 1), то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки.
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу и найти приближенное значение функций в этой точке.
Линейная интерполяция
В частности, для i - го интервала можно написать уравнение прямой, проходящей через точки (xi , yi) и (xi + 1, yi + 1), в виде:
Слайд 9
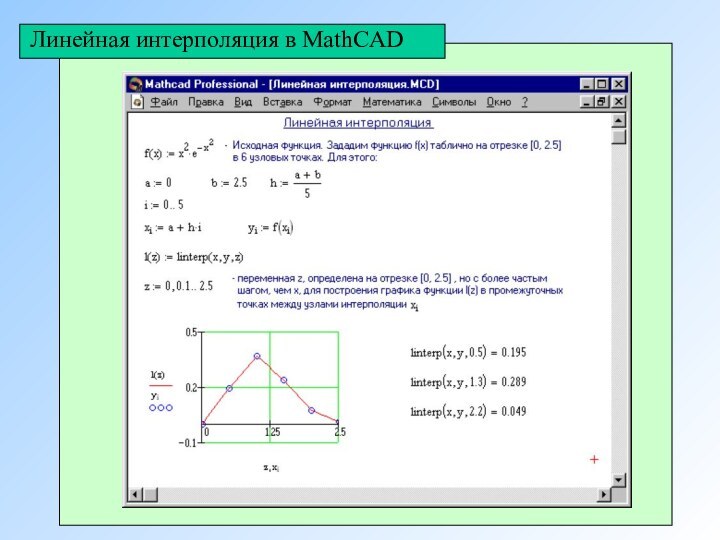
Линейная интерполяция в MathCAD
При линейной интерполяции MathCAD соединяет
существующие точки данных прямыми линиями (соединяет точки данных отрезками
прямых, создавая таким образом ломаную). Это выполняется функцией linterp.
Слайд 11
Наиболее широкое практическое применение, в силу их простоты,
нашли кубические сплайны. Основные идеи теории кубических сплайнов сформировались
в результате попыток математически описать гибкие рейки из упругого материала (механические сплайны), которыми издавна пользовались чертежники в тех случаях, когда возникала необходимость проведения через заданные точки достаточно гладкой кривой. Известно, что рейка из упругого материала, закрепленная в некоторых точках и находящаяся в положении равновесия, принимает форму, при которой ее энергия является минимальной.Кубическая сплайн-интерполяция
Теория сплайнов - новый раздел современной вычислительной математики, интенсивно развивающийся в последние годы.
Линейная интерполяция, по существу, является простейшим сплайном первой степени, квадратичная интерполяция - второй.
Сплайны позволяют эффективно решать задачи обработки экспериментальных зависимостей между параметрами, имеющих достаточно сложную структуру.
Это фундаментальное свойство позволяет эффективно использовать сплайны при решении практических задач обработки экспериментальной информации.
Слайд 12
В общем случае для функции y = f(x)
требуется найти приближение y = φ (x) таким образом,
чтобы f (xi) = φ (xi) в точках x = xi, a в остальных точках отрезка [a, b] значения функций f(x) и φ (x) были близкими между собой.
Слайд 14
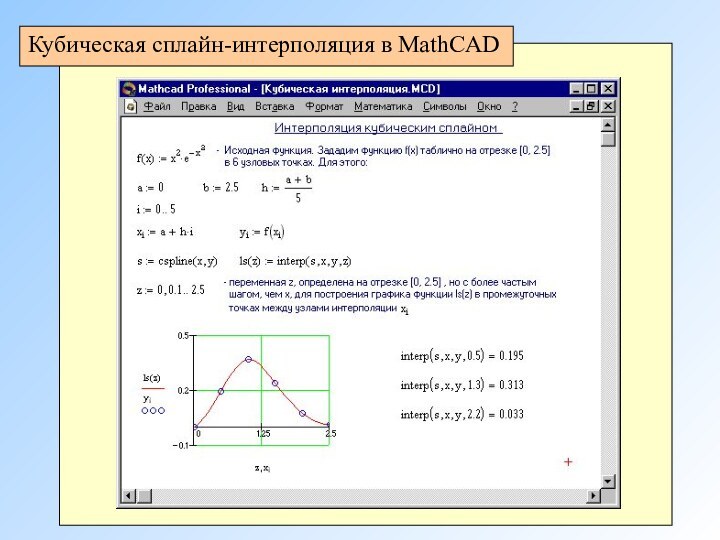
Кубическая сплайн-интерполяция в MathCAD
Проводит кривую через набор точек
таким образом, что первые и вторые производные кривой непрерывны
в каждой точке. Кривая образуется путем создания ряда кубических полиномов, проходящих через наборы из трех смежных точек. Кубические полиномы затем состыковываются друг с другом, чтобы образовать одну кривую.interp(vs, vx, vy, x) - возвращает интерполируемое значение y, соответствующее аргументу x. Вектор vs вычисляется на основе векторов данных vx и vy по одной из функций pspline, lspline или cspline.
Слайд 15
Построения кубического сплайна через набор точек:
Создать векторы vx
и vy, содержащие координаты x и y, через которые
нужно провести кубический сплайн. Элементы vx должны быть расположены в порядке возрастания.Вычислить вектор vs = cspline(vx,vy). Вектор vs содержит вторые производные интерполяционной кривой в рассматриваемых точках. Чтобы найти интерполируемое значение в произвольной точке x0 , вычислите
interp(vs, vx, vy, x0) , где vx, vy - векторы, описанные ранее.
или
Вычислить interp(cspline(vx, vy),vx, vy, x0)
Слайд 17
Можно использовать оператор векторизации, чтобы вычислить сразу целый
набор интерполируемых значений, соответствую-щих вектору заданных точек. Это можно
сделать и с interp, и с linter.Интерполяция вектора точек
На примере показано, как выполнить эту операцию. Чтобы применить оператор векторизации к функции, щелкните мышью на имени функции и нажимайте клавишу пробел, пока в рамку не попадет нужная функция. Затем нажмите Ctrl + - (минус).
Слайд 18
Функция predict В Mathcad позволяет оценить значения формул
в точках, находящихся вне области расположения сетки, на которой
заданы значения функции. Эта функция использует линейный алгоритм предсказания, который является полезным, когда экстраполируемая функция является гладкой и осциллирующей, хотя не обязательно периодической. Линейное предсказание можно рассматривать как разновидность экстраполяции, но нельзя путать с линейной или полиномиальной экстраполяцией.Линейное предсказание (экстраполяция)