- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы решения логарифмических уравнений
Содержание
- 2. ПланВведениеИсторическая справка Определение уравнения, виды уравнений Свойства функций Нестандартные методы решения уравнений Заключение
- 3. Актуальность Актуальность моей работы заключается
- 4. Цель моей работы- ознакомление с нестандартными методами
- 5. Задачи: собрать сведения из истории математики о
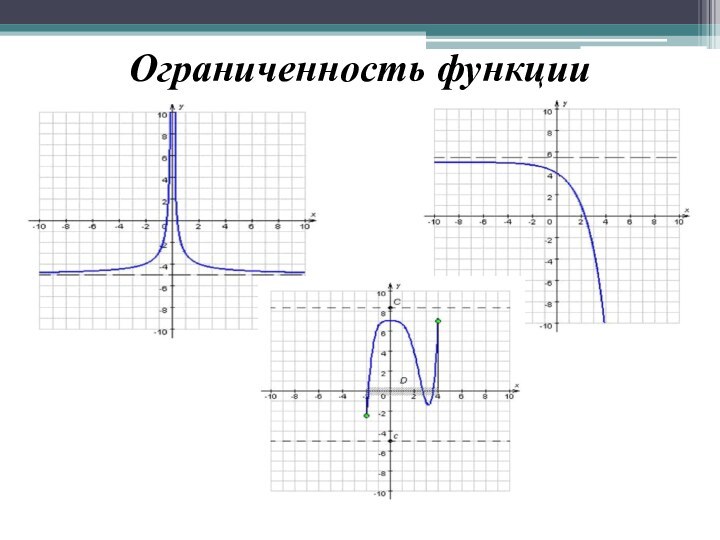
- 6. Ограниченность функции
- 7. Пример 1 Решите уравнение.
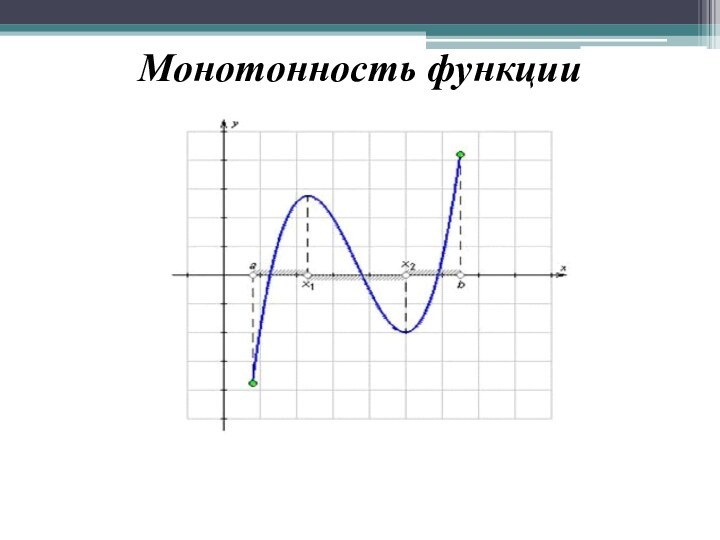
- 8. Монотонность функции
- 9. Теорема о корне. Пусть функция f
- 10. Решите уравнение. Пример 2
- 11. f(f(x))=x f(x)=xЕсли функция f(x) возрастающая ,то уравнение
- 12. Пример 3 Решите уравнение
- 13. ОДЗПример 4Решите уравнение:
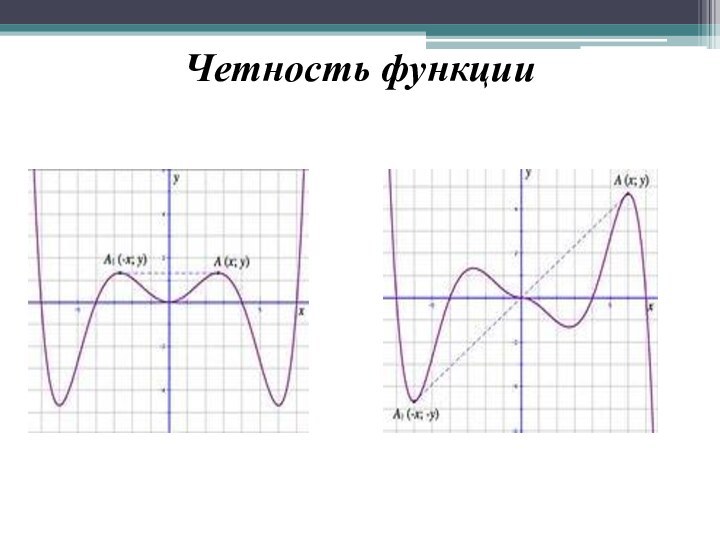
- 14. Четность функции
- 15. В основе рассматриваемого способа лежит формула :(
- 16. Пример 6Решите уравнение.Решение:Домножим левую и правую части
- 17. Алгоритм:1.Найдем середину отрезка
- 18. ЗаключениеВ процессе работы над темой «Нестандартные методы
- 19. Скачать презентацию
- 20. Похожие презентации
ПланВведениеИсторическая справка Определение уравнения, виды уравнений Свойства функций Нестандартные методы решения уравнений Заключение
















Слайд 2
План
Введение
Историческая справка
Определение уравнения, виды уравнений
Свойства функций
Нестандартные методы решения уравнений
Слайд 3
Актуальность
Актуальность моей работы заключается в
том, что приобретенные знания и навыки будут в дальнейшем
использованы в работе ЕГЭ, в будущей профессии, в различных жизненных ситуациях.Слайд 4 Цель моей работы- ознакомление с нестандартными методами решения
уравнений, в частности, на этот год- для решения иррациональных
уравнений
Слайд 5
Задачи:
собрать сведения из истории математики о решении
уравнений
применить имеющиеся знания по теме «Функция» к решению иррациональных
уравнений изучить теорию по нестандартным методам решения иррациональных уравнений (в перспективе и другие виды уравнений: тригонометрические , логарифмические и т.д.).
Слайд 7
Пример 1
Решите уравнение.
+ -
= 5+2х
Решение. Перепишем уравнение:
+
=
5+2х
+
Пусть t=
Тогда
Наибольшее значение подкоренного выражения достигается при x=-1(в вершине параболы y=15-2x- ).При этом t2 =16.Отсюда следует, что 4.Наименьшее значение правой части исходного уравнения достигается также при х=-1 и тоже равно 4.При левая часть(когда она существует) меньше правой.
+
= 8+2
Слайд 9
Теорема о корне.
Пусть функция f возрастает
(или убывает) на промежутке I, число а - любое
из значений, принимаемых f на этом промежутке. Тогда уравнение f(x)=a имеет единственный корень на этом промежутке I.Доказательство. Рассмотрим возрастающую функцию f (в случае, если f - убывающая функция, рассуждения аналогичны). По условию в промежутке I существует такое число b, что f(b)=a. Надо показать, что b - единственный корень уравнения f(x)=a. Допустим, что на промежутке I есть еще число c ≠ b, такое, что f(c)=a. Тогда или c < b или c > b. Но функция f возрастает на промежутке I, поэтому соответственно либо f(c) < f(b), либо f(c) > f(b). Это противоречит равенству f(c)=f(b)=a. Следовательно, сделанное предположение неверно и кроме числа b, других корней на промежутке I у уравнения f(x)=a нет.
Слайд 10
Решите уравнение.
Пример 2
+
+
=9
Решение.
Заметим, что левая часть уравнения — возрастающая функция. Но
это значит, что больше одного корня такое уравнение иметь не может.Итак,х=1 -единственный корень.Ответ:1
Слайд 11
f(f(x))=x f(x)=x
Если функция f(x) возрастающая ,то уравнение
f(f(x))=x равносильно уравнению f(x)=x.
Доказательство. Всякий корень уравнения f(x)=x
есть корень уравнения f(f(x))=x. Пусть х0 -корень уравнения f(f(x))=x, причем .Тогда либо ,но при этом f(f(x0))= , противоречие; либо , но в этом случае х 0 =f(f ,т.е. х 0
Слайд 12
Пример 3
Решите уравнение
=х
Пусть f(x)= .Наше уравнение имеет вид
f(f(x))=x
Чтобы завершить решение, достаточно решить уравнение
х=.
. Ответ:.
.
.
.
Слайд 13
ОДЗ
Пример 4
Решите уравнение:
+
Решение:
4-
х-2
х+7
4х+1
x=2
В области определения данного уравнения должны
одновременно выполняться неравенства 4- и ,что возможно только при х=2.Проверкой убеждаемся ,что 2 -корень.Ответ:2.
-
=
Слайд 15
В основе рассматриваемого способа лежит формула :
(
- ) ( + )
=a-bВыражения - и + мы будем называть
сопряженными.Иногда использование этой формулы
облегчает решение.
Умножение на сопряженное
Слайд 16
Пример 6
Решите уравнение.
Решение:
Домножим левую и правую части уравнения
на сумму радикалов стоящих в левой части. Получается уравнение:
равносильное
такому:откуда либо х= , либо
Последнее уравнение решим уже рассмотренным способом: пусть
Тогда приходим к уравнению :
Откуда t= , а х=
Ответ: ,
–
= 2x-1
2(2х-1)=(2х-1)(
+
)
(2х-1)(2-(
+
))=0
,
+
=2.
t=
.
= 2-t
,
:
;
Слайд 17
Алгоритм:
1.Найдем середину отрезка
: с = (a+b):2
2. Вычислим значения функции в точках
a и c и найдем произведениеполученных значений : d=f(c)?f(a)
3. Если d>0,то теперь точкой a станет c:a=c;
Если d<0,то точкой b станет c:b=c;
4. Вычислим разность a и b ,сравним ее,если меньше 0
то идем в пункт 1,если нет, то корень с нужной нам точностью найден,
и он равен : x=(a+b)/2.
Метод половинного деления
Слайд 18
Заключение
В процессе работы над темой «Нестандартные методы решения
иррациональных уравнений» я узнала новые теоремы ,научилась применять свойства
функций к решению иррациональных уравнений , нашла множество применений данных знаний в решении сложных жизненных задач в разных сферах науки : экономике, строительстве, транспорте.Данные методы значительно облегчают решение уравнений.
В жизни нужно не только следовать инструкциям, но уметь действовать по ситуации - применять все имеющиеся знания, т.е. иметь «вторую грамотность» - знания в действии.





























