- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
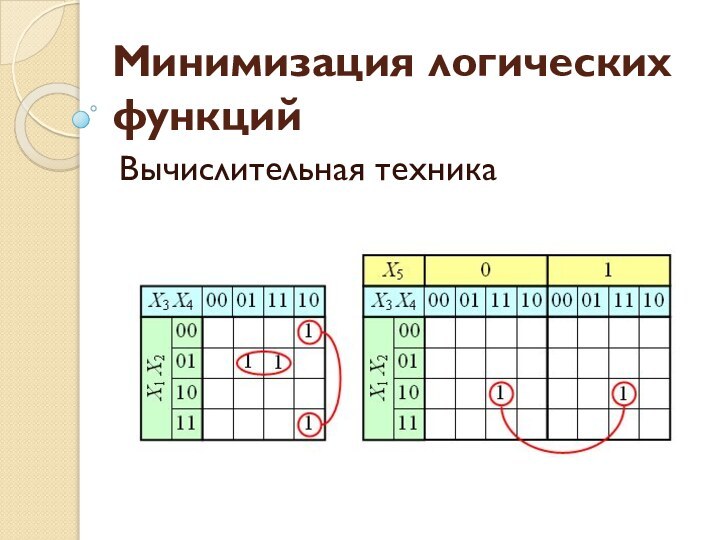
Презентация на тему Минимизация логических функций. Вычислительная техника
Содержание
- 2. Минимизация упрощение формы записисхема реализуется с наименьшим числом элементов
- 3. Минимальная нормальная формаНормальная форма логической функции, содержащая
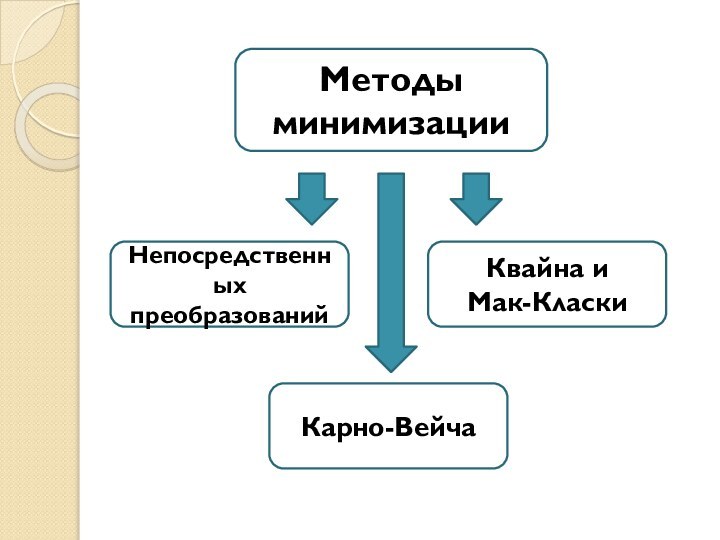
- 4. Методы минимизацииНепосредственных преобразованийКвайна и Мак-КласкиКарно-Вейча
- 5. МЕТОД НЕПОСРЕДСТВЕННЫХ ПРЕОБРАЗОВАНИЙ Минимизация логических функций
- 6. Метод непосредственных преобразований Применение законов алгебры логики Результат − тупиковая форма логической функции
- 7. Тупиковая формаЛогическое выражение, к слагаемым которого больше
- 8. Функции a и b называются равносильными, если
- 9. ЗАКОНЫ ЛОГИКИ
- 10. 1. Идемпотентностьa & a ≡ a a ∨ a ≡ a
- 11. 2. Коммутативностьa & b ≡ b & aa ∨ b ≡ b ∨ a
- 12. 3. Ассоциативностьa & (b & с) ≡
- 13. 4. Дистрибутивностьa & (b∨с) ≡ (a &
- 14. 5. Закон двойного отрицания¬(¬a) ≡ a
- 15. 6. Законы поглощенияa & (a ∨ b) ≡ aa ∨ (a & b) ≡ a
- 16. 7. Законы де Моргана¬(a ∨ b) ≡
- 17. 8. Закон исключённого третьего¬a ∨ a ≡ 1
- 18. 9. Закон противоречия¬a & a ≡ 0
- 19. 10. Свойства тавтологии и противоречия1 & a
- 20. 11. Законы склеивания(a & b) ∨ (a
- 21. 12. Законы поглощенияa & (a ∨ b) ≡ aa ∨ (a & b) ≡ a
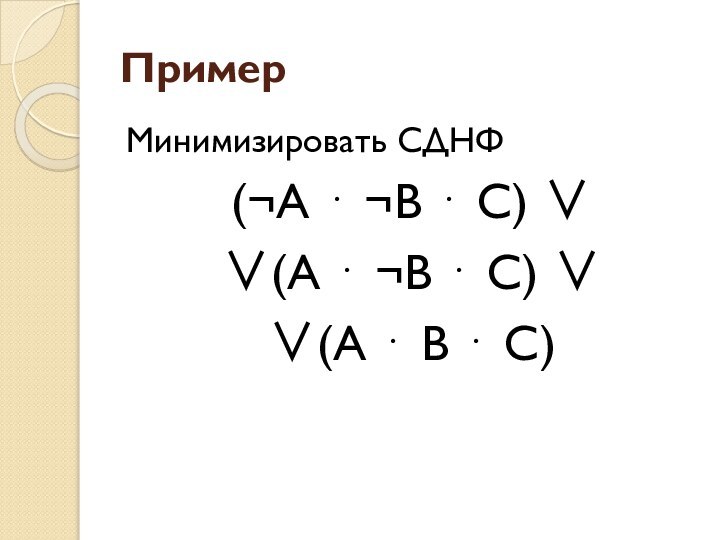
- 22. ПримерМинимизировать СДНФ(¬А ⋅ ¬В ⋅ С) ∨∨(А ⋅ ¬В ⋅ С) ∨∨(А ⋅ В ⋅ С)
- 23. Пример(¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨∨(А ⋅ В ⋅ С) ≡
- 24. Пример(¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨∨(А ⋅ В ⋅ С) ≡
- 25. Пример(¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В ⋅ С) ∨∨(А ⋅ В ⋅ С) ≡
- 26. Пример(¬А ⋅ ¬В ⋅ С) ∨(А ⋅
- 27. Пример(¬А ⋅ ¬В ⋅ С) ∨(А ⋅
- 30. ПроблемаОпределить, какие элементарные конъюнкции / дизъюнкции надо склеивать
- 31. КАРТЫ ВЕЙЧА-КАРНОМинимизация логических функций
- 32. Эдвард Вестбрук ВейчАмериканский физик1952 «Метод диаграмм для минимизации логических функций»1924 — 2013
- 33. Морис Карнород. 1924Американский физик1953Усовершенствовал метод Вейча
- 34. Карта КарноГрафическое представление таблицы истинности логических функций
- 35. Код Грея система счисления, в которой два соседних значения различаются только в одном разряде
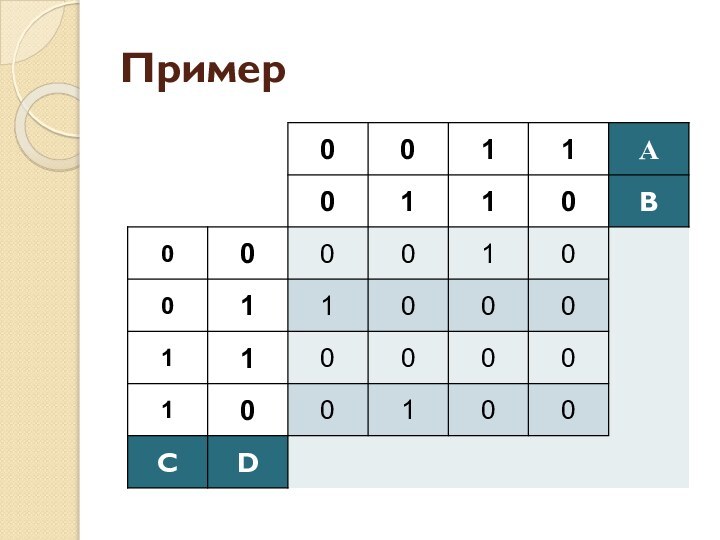
- 36. Пример
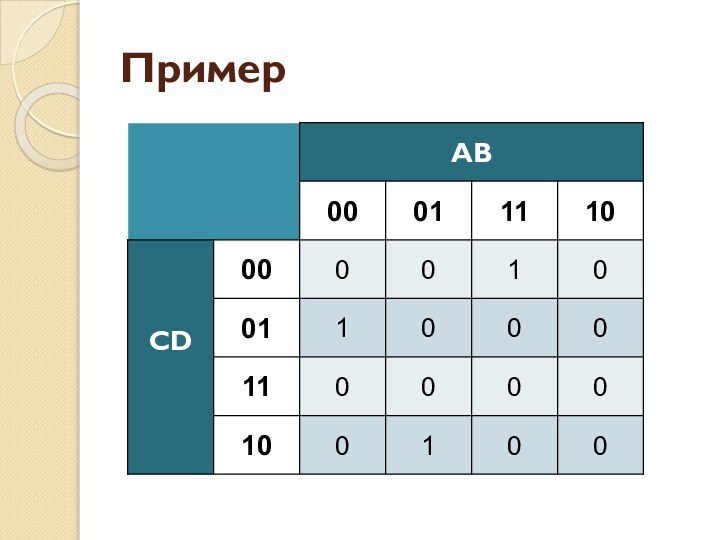
- 37. Пример
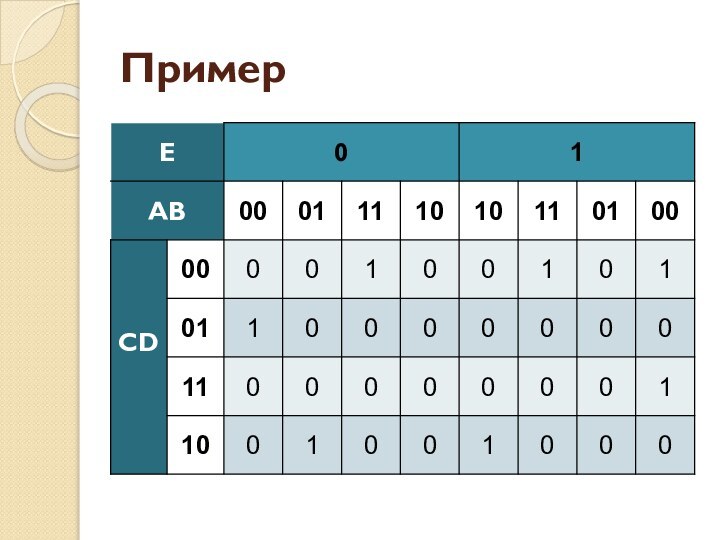
- 38. Пример
- 39. Пример
- 41. Пример
- 42. Пример
- 43. Пример
- 44. Правила ДНФ КНФ1. Объединяем
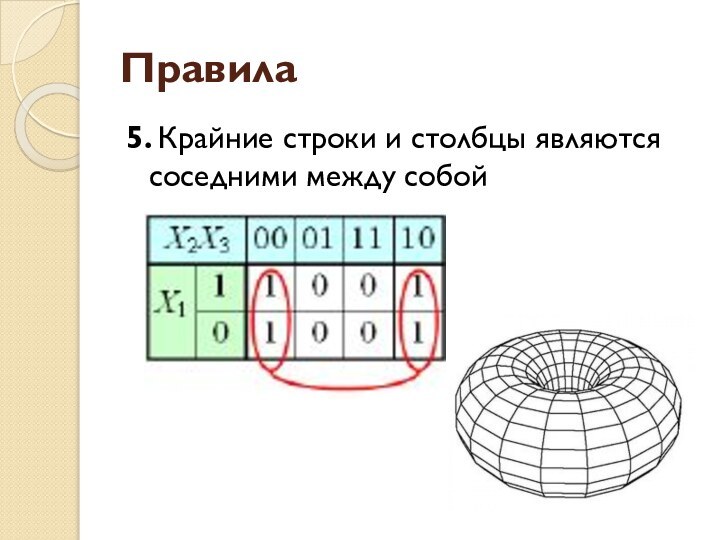
- 45. Правила5. Крайние строки и столбцы являются соседними между собой
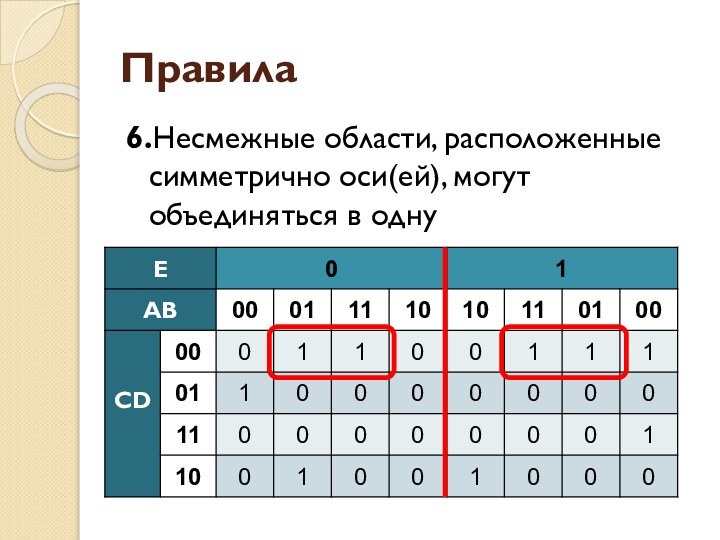
- 46. Правила6.Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну
- 47. Правила 7. Для каждой области записываем конъюнкцию
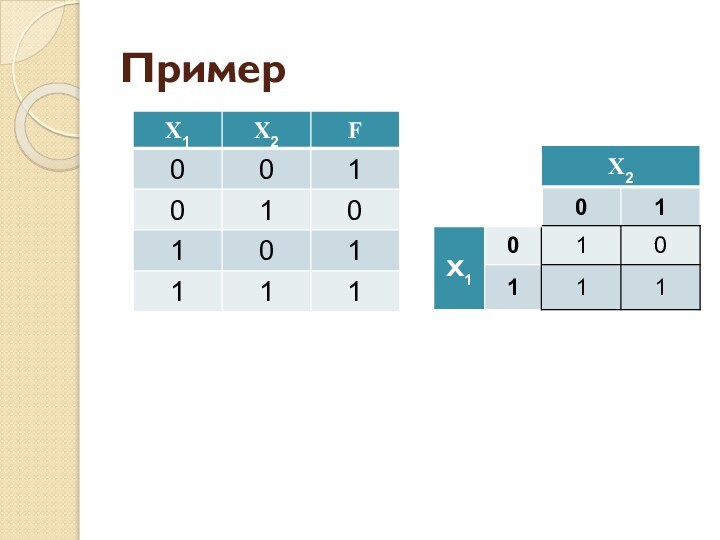
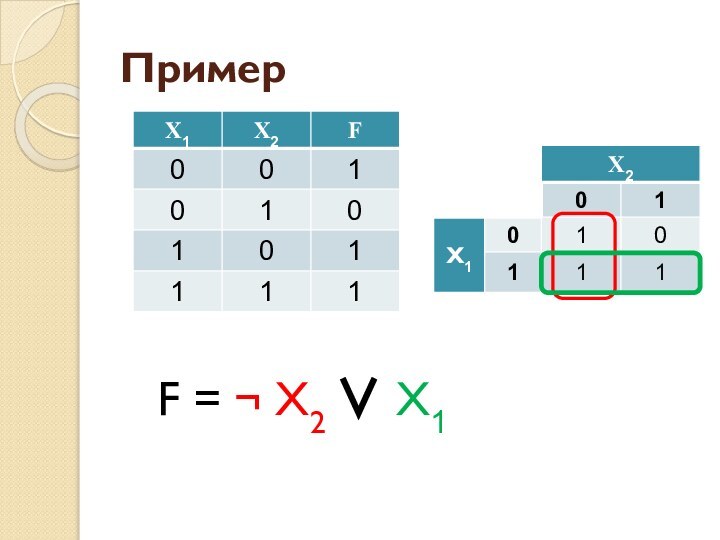
- 48. ПримерF = ¬ X2 ∨ X1
- 49. Пример ‒ МДНФF = X1 ⋅¬ X2 ∨ ¬X1⋅ X2
- 50. Пример ‒ МКНФF = (X1 ∨ X2) ⋅ (¬X1∨ ¬ X2)
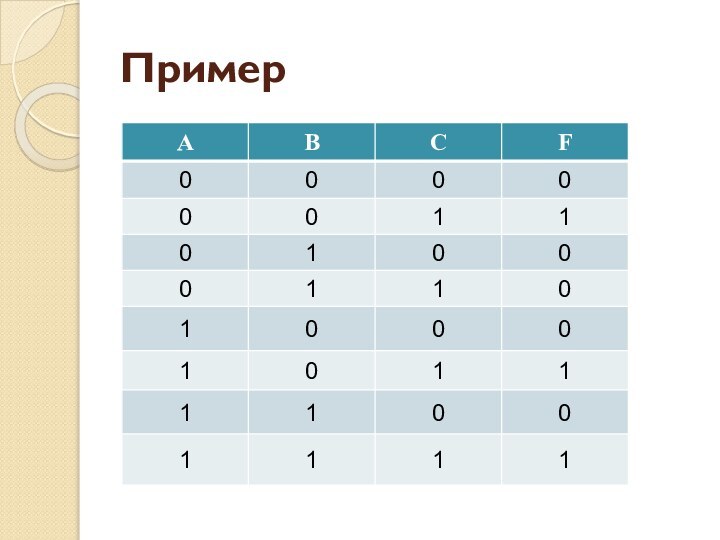
- 51. Пример
- 52. Формула(¬А ⋅ ¬В ⋅ С) ∨∨(А ⋅
- 53. (А ∨ В ∨ С) ⋅⋅ (А
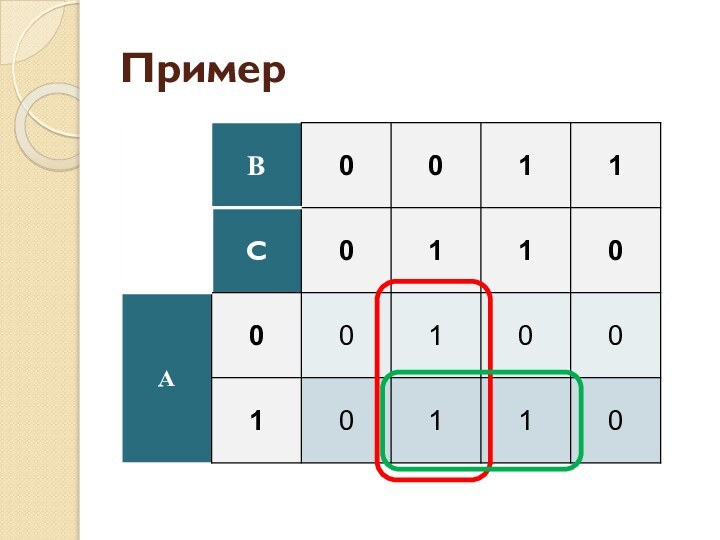
- 54. Пример
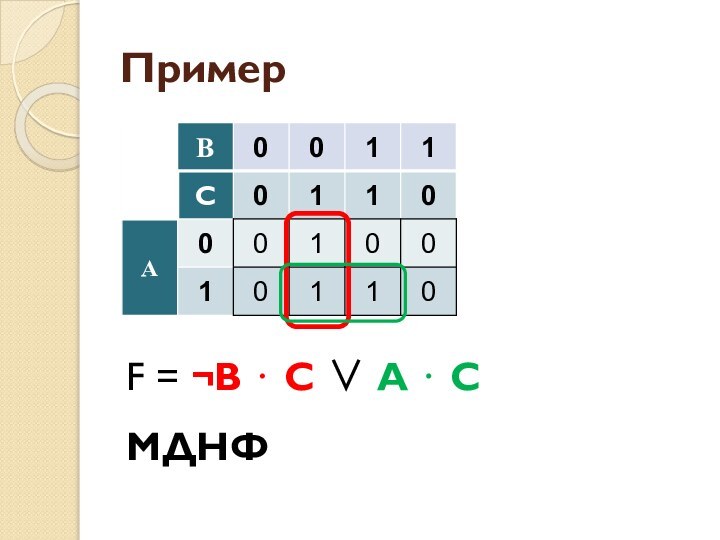
- 55. ПримерF = ¬В ⋅ С ∨ A ⋅ CМДНФ
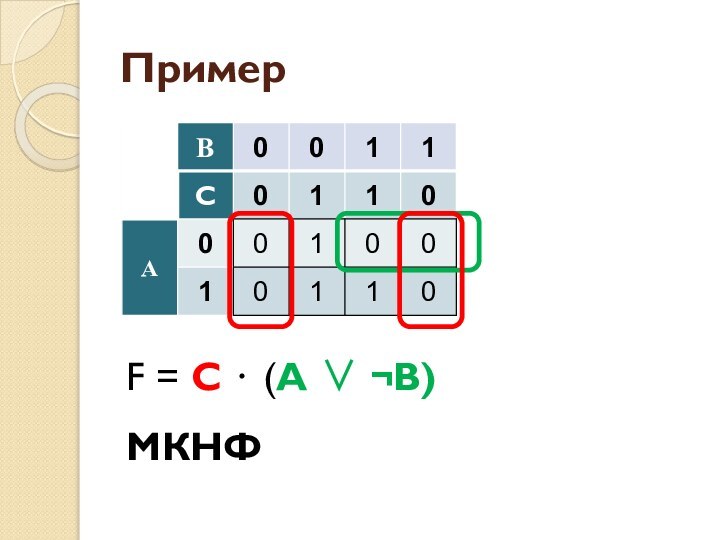
- 56. ПримерF = С ⋅ (A ∨ ¬В)МКНФ
- 58. НедостаткиПрименим для функций до 7 переменныхВыбор областей ‒ визуальноНет алгоритма, обеспечивающего оптимальное решение
- 59. МЕТОД КВАЙНА И МАК-КЛАСКИ Минимизация логических функций
- 60. Виллард ван Орман КуайнАмериканский философ, логик и
- 61. Эдвард Дж. Мак-КласкиПочётный профессор Стэнфордского университета.Пионер в области электротехникиПервый алгоритм проектирования комбинационных схем1908 — 2000
- 62. Скачать презентацию
- 63. Похожие презентации
Минимизация упрощение формы записисхема реализуется с наименьшим числом элементов





























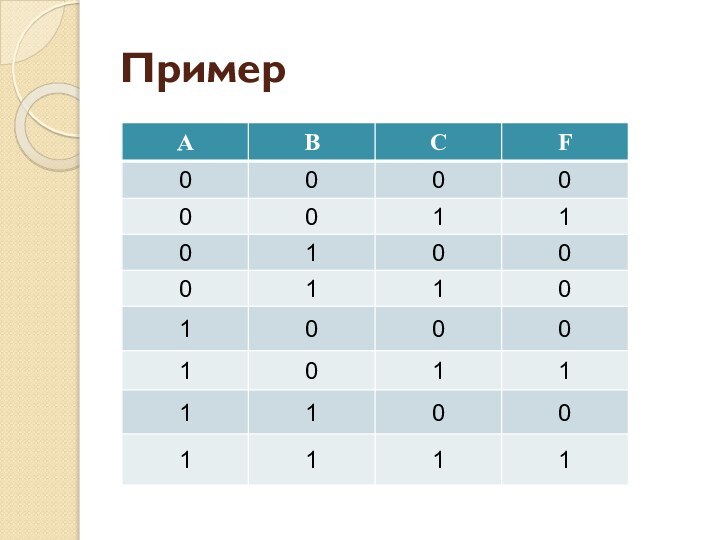
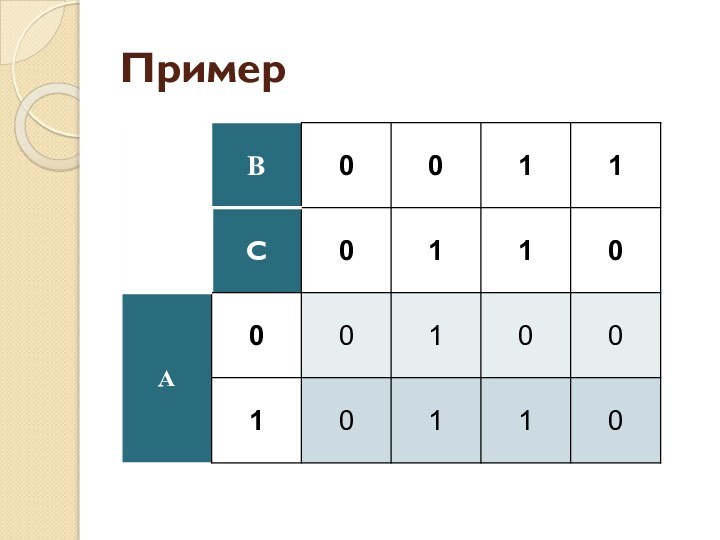
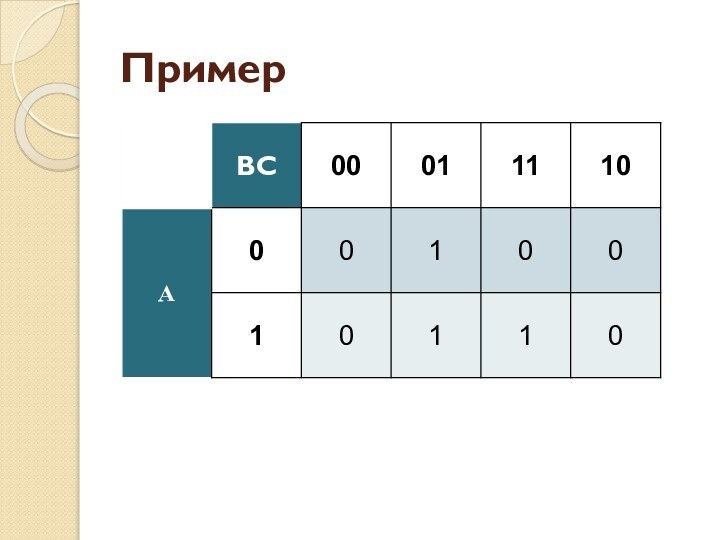
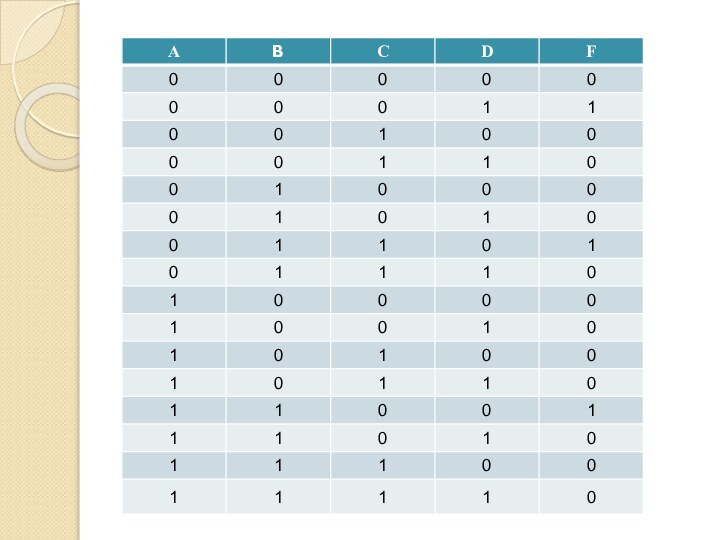











Слайд 3
Минимальная нормальная форма
Нормальная форма логической функции, содержащая наименьшее
число элементов
Минимальная ДНФ = МДНФ
Минимальная КНФ = МКНФ
Логическая функция
может иметь несколько МДНФ или МКНФ одинаковой сложности
Слайд 6
Метод непосредственных преобразований
Применение законов алгебры логики
Результат
− тупиковая форма логической функции
Слайд 7
Тупиковая форма
Логическое выражение, к слагаемым которого больше не
могут быть применены операции склеивания
Для одной функции может существовать
несколько тупиковых формМинимальная форма − тупиковая форма логической функции минимальной длины
Слайд 8 Функции a и b называются равносильными, если при
одинаковых входных данных они принимают одинаковые значения
a ≡ b
Слайд 19
10. Свойства тавтологии и противоречия
1 & a ≡
a 1 ∨ a ≡ 1
0 &
a ≡ 0 0 ∨ a ≡ a¬ 0 ≡ 1 ¬ 1 ≡ 0
Слайд 26
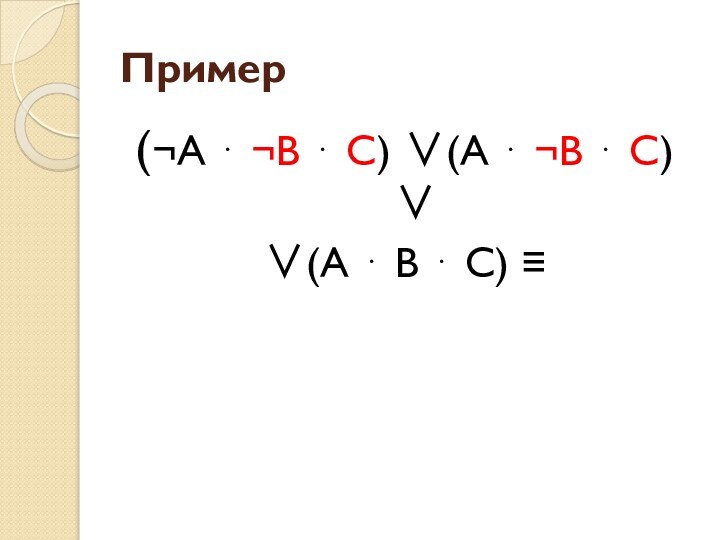
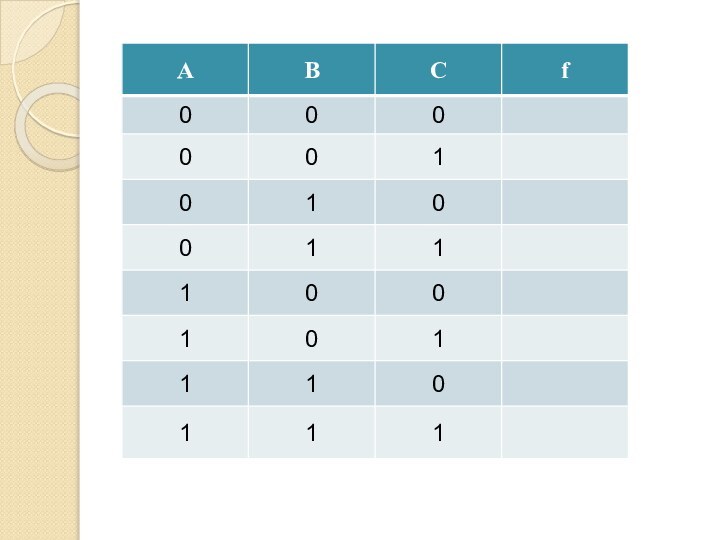
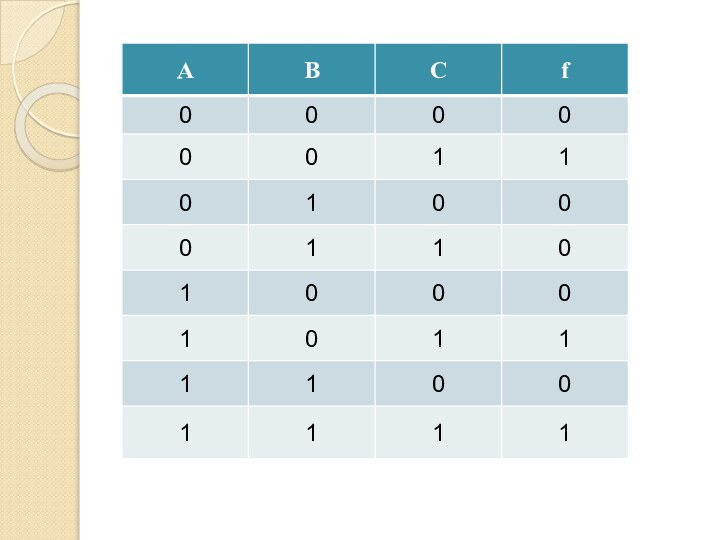
Пример
(¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В
⋅ С) ∨
∨(А ⋅ В ⋅ С) ≡
(¬А ⋅
¬В ⋅ С) ∨ (А ⋅ ¬В ⋅ С) ∨ ∨ (А ⋅ ¬В ⋅ С) ∨ (А ⋅ В ⋅ С)
Слайд 27
Пример
(¬А ⋅ ¬В ⋅ С) ∨(А ⋅ ¬В
⋅ С) ∨
∨(А ⋅ В ⋅ С) ≡
(¬А ⋅
¬В ⋅ С) ∨ (А ⋅ ¬В ⋅ С) ∨ ∨(А ⋅ ¬В ⋅ С) ∨ (А ⋅ В ⋅ С)
≡ (¬В ⋅ С) ∨ (А ⋅ С) ≡
≡ С ⋅ (А ∨ ¬В)
Слайд 32
Эдвард Вестбрук Вейч
Американский физик
1952
«Метод диаграмм для минимизации
логических функций»
1924 — 2013
Слайд 34
Карта Карно
Графическое представление таблицы истинности логических функций
Таблица,
содержащая по 2n прямоугольных ячеек,
где n — число
логических переменных
Слайд 35
Код Грея
система счисления, в которой два соседних
значения различаются только в одном разряде
Слайд 44
Правила
ДНФ КНФ
1. Объединяем смежные
клетки с единицами (нулями) в максимально возможные области, содержащие
2n клеток2. В области НЕ должно находиться клеток, содержащих нули (единицы)
3. Области могут пересекаться
4. Возможно несколько вариантов покрытия
Слайд 47
Правила
7. Для каждой области записываем конъюнкцию (дизъюнкцию)
переменных, не изменяющих своё значение
Если неизменная переменная равна
нулю (единице) − инвертируем8.Конъюнкции (дизъюнкции) областей объединяем дизъюнкцией (конъюнкцией).
Слайд 52
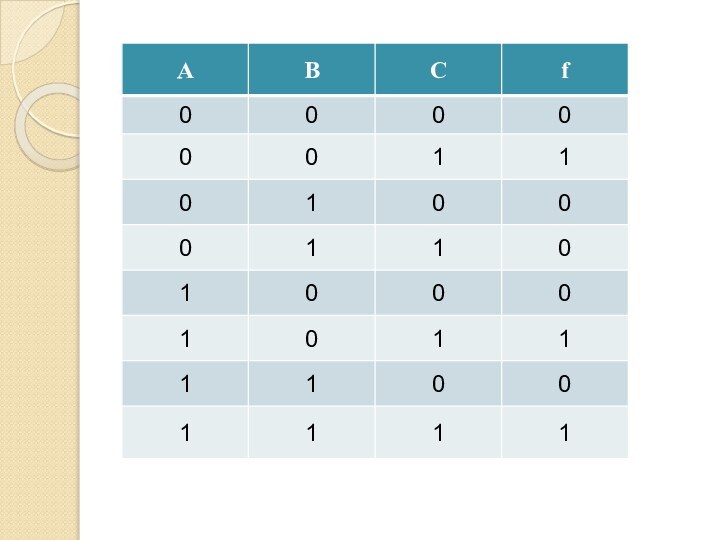
Формула
(¬А ⋅ ¬В ⋅ С) ∨
∨(А ⋅ ¬В
⋅ С) ∨
∨(А ⋅ В ⋅ С)
Совершенная дизъюнктивная нормальная
форма (СДНФ)
Слайд 53
(А ∨ В ∨ С) ⋅
⋅ (А ∨
¬В ∨ С) ⋅
⋅ (А ∨¬ В ∨ ¬С)
⋅⋅ (¬А ∨ В ∨ С) ⋅
⋅ (¬А ∨ ¬В ∨ С)
Совершенная конъюнктивная нормальная форма (СКНФ)