конечного числа многоугольников.
Виды многогранников:
1 Платоновы тела
2 Архимедовы
тела3 Тела Кеплера-Пуансо
Многогранники
в архитектуре
Многогранники
в искусстве
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





































Многогранники
в архитектуре
Многогранники
в искусстве
Существование пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
А так как пятой стихии в природе не было, то по их учению додекаэдр представлял собой всю Вселенную, то есть они считали, что мы живём внутри небесного свода, имеющего форму поверхности правильного додекаэдра.
Пять элементов
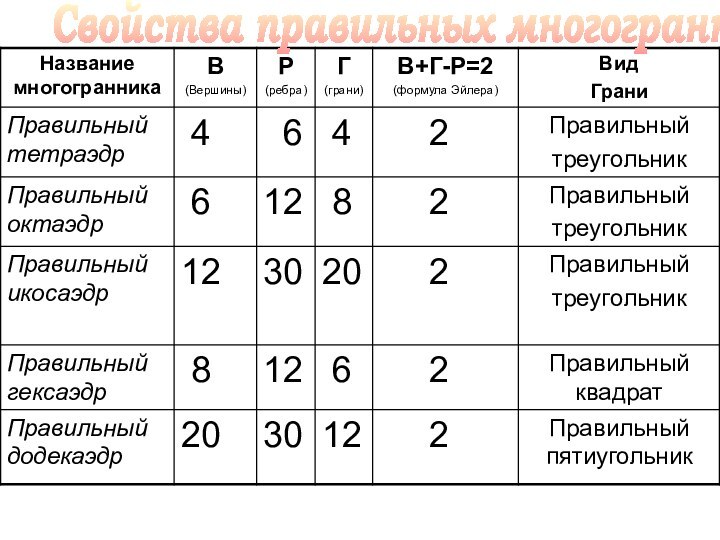
S =6a2
V =a3
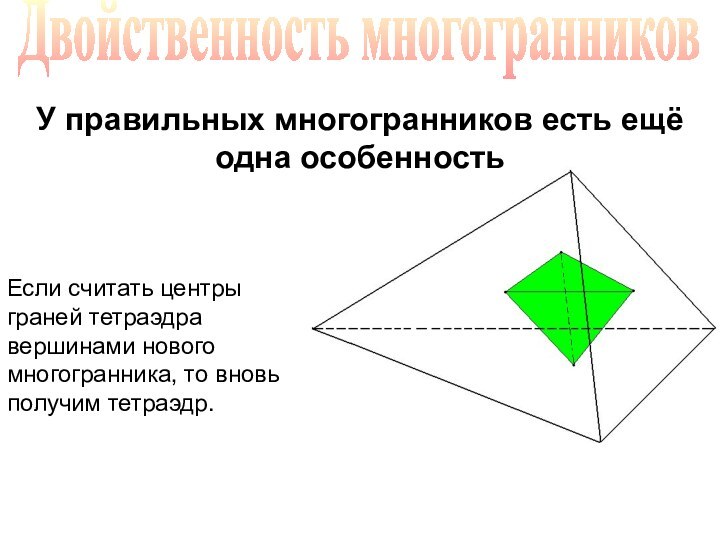
Если считать центры граней тетраэдра вершинами нового многогранника, то вновь получим тетраэдр.
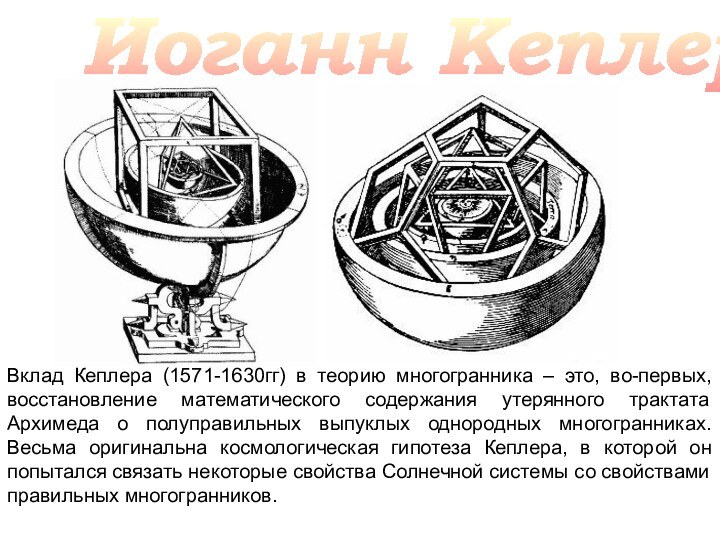
Открытие тринадцати полуправильных многогранников приписывается Архимеду, впервые перечислившего их в недошедшей до нас работе.
Было предложение Кеплера рассматривать невыпуклые многогранники со звёздчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра. Поэтому эта группа многогранников носит название тела Кеплера - Пуансо.