и возрастание функции.
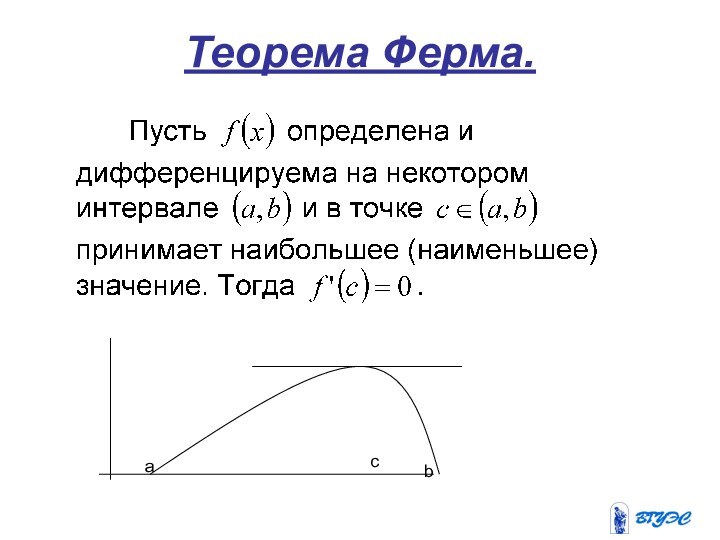
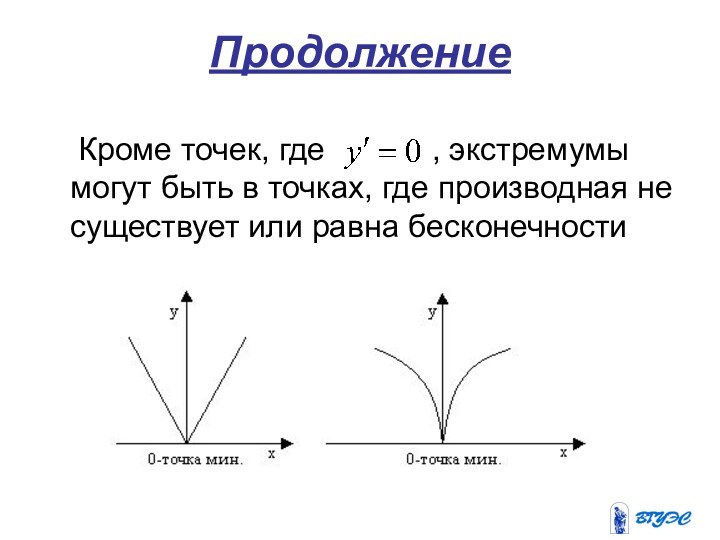
4. Экстремумы.
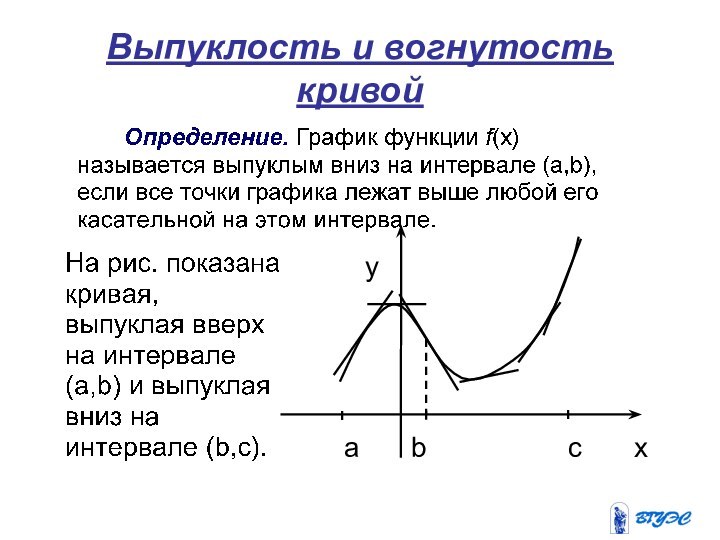
5. Выпуклость и вогнутость графика функции.
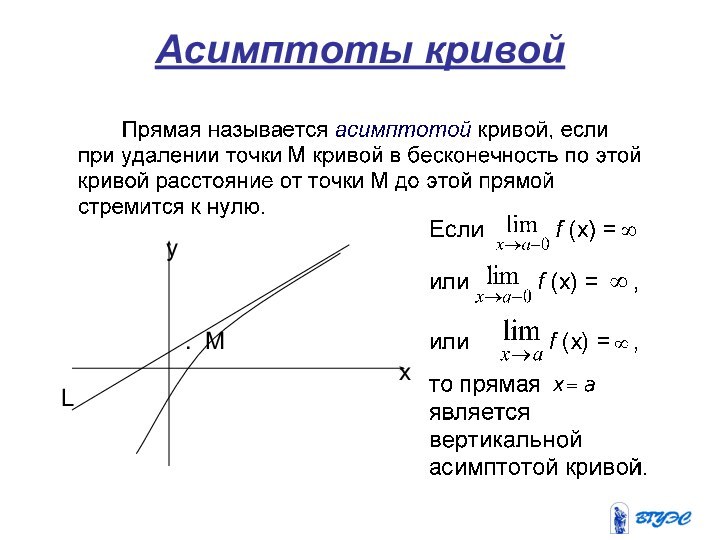
Точки перегиба.6. Асимптоты.
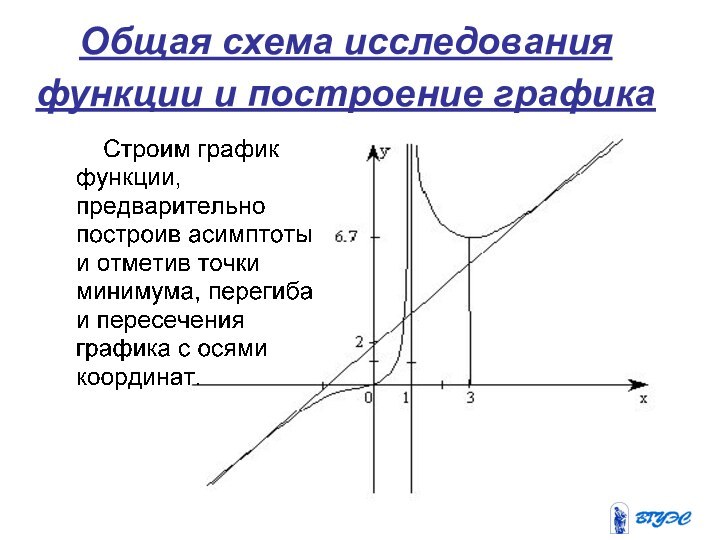
7. Общая схема исследования функции и построение графика.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

































a
b
f(a)
f(b)