Презентация на тему Многогранники

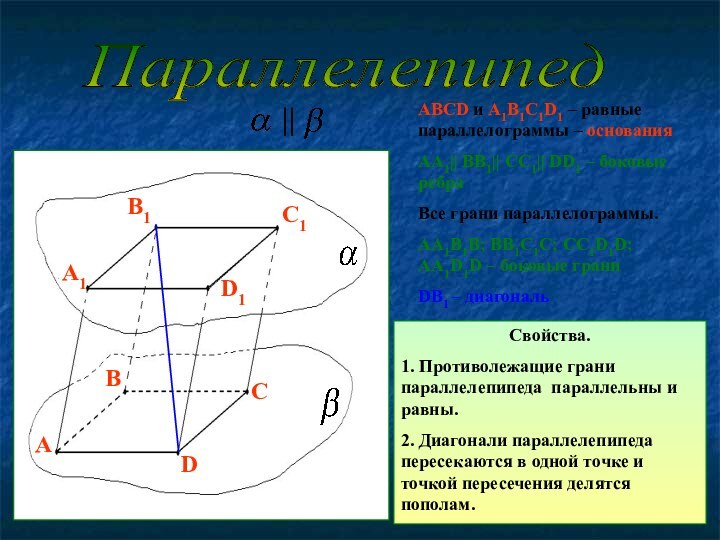
основания
АА1|| ВВ1|| СС1|| DD1 – боковые ребра
Все

Свойства.
1. Противолежащие грани параллелепипеда параллельны и равны.
2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

А

В

С

D

А1

В1

С1

D1

боковые грани являются прямоугольниками.
А
В
С
D
A1
B1
С1
D1
a
b
c

грани прямоугольники.
а
b
c
a – длина, b – ширина,
с –

d

d2 = a2 + b2 + c2

лежащие в параллельных плоскостях, боковые грани – параллелограммы.
Наклонная

H

H1

A

k

F

M

N

P

D

HH1 – высота призмы
AH (k) – боковое ребро призмы
FMNPD – сечение, перпендикулярное боковому ребру

а
а
а
d
все грани - квадраты
H

(основание) и n треугольников (боковые грани), имеющих общую вершину

Р

А1

А2

А3

Аn

H

РА1; РА2; РА3; ... ; РАn – боковые ребра
А1А2; ... ;А1Аn – ребра основания
РH – высота пирамиды - h

h

проецируется в центр основания;
боковые ребра – равны;
боковые

H – высота,

h – апофема

H

h

пирамида
H – высота,

h – апофема

A
O
B
C
h
H
S
D
a

AB = BC = CD = DA = a

H

h

a

a

A

B

D

O

P

К

К – середина DC

C

а – сторона основания

секущая плоскость,
PB1B2…Bn – пирамида
Усеченная пирамида
β
α

P
A1
A2
A3
An
B1
B3
Bn
B2
O
O1
H
B1B2…Bn –

равные между собой равнобокие трапеции.
Δ ABC и Δ A1B1C1

A

C

A1

B1

C1

O1

O

H

K1

K

h

B

a

b