- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Многомерное шкалирование. Статистические методы в психологии
Содержание
- 2. Многомерное шкалированиеМногомерное шкалирование (МШ) можно рассматривать как альтернативу факторному анализу.
- 3. Многомерное шкалированиеЦелью является поиск и интерпретация «латентных»
- 4. Многомерное шкалированиеОсновная цель:Выявление структуры исследуемого множества объектов(структура
- 5. Многомерное шкалированиеИсходная информация для МШ – данные о различии или близости объектов
- 6. Многомерное шкалированиеВ психологии исходными данными для МШ
- 7. Многомерное шкалированиеСчитается, что в основе таких суждений
- 8. Многомерное шкалированиеОсновная задача МШ:Реконструкция психологического пространства, заданного
- 9. Многомерное шкалированиеПоэтому шкала в МШ интерпретируется как критерий, лежащий в основе различий стимулов.
- 10. Основная идеяПример: пусть имеется матрица попарных расстояний
- 11. Основная идеяВ общем случае метод МНШ позволяет
- 12. Основная идея В результате можно "измерить" эти
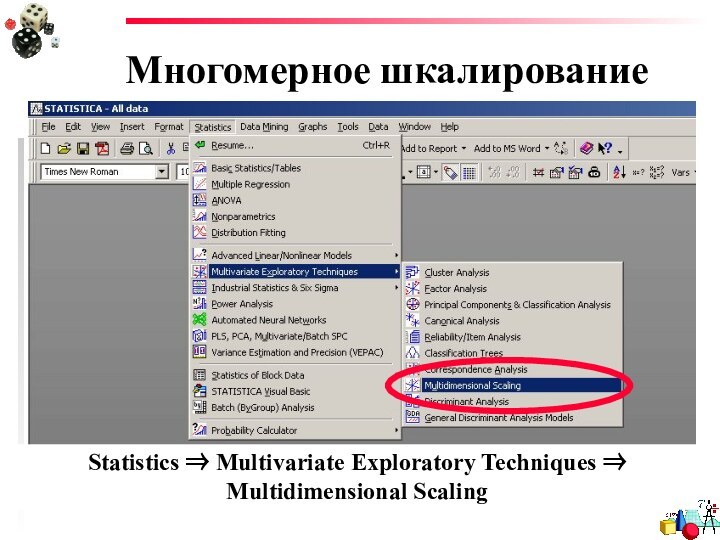
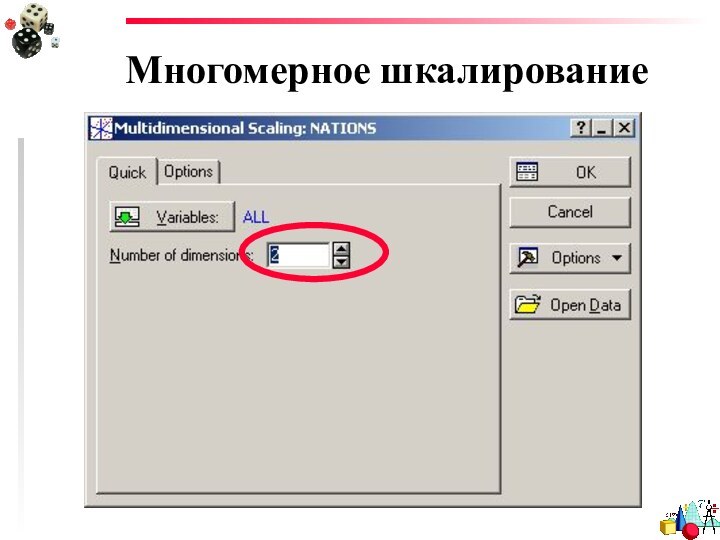
- 13. Многомерное шкалированиеStatistics ⇒ Multivariate Exploratory Techniques ⇒ Multidimensional Scaling
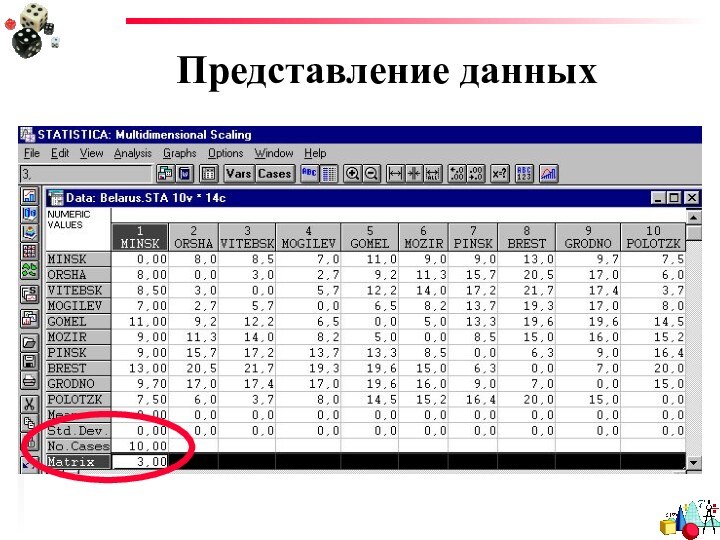
- 14. Представление данных
- 15. Представление данныхМатрица может представлять
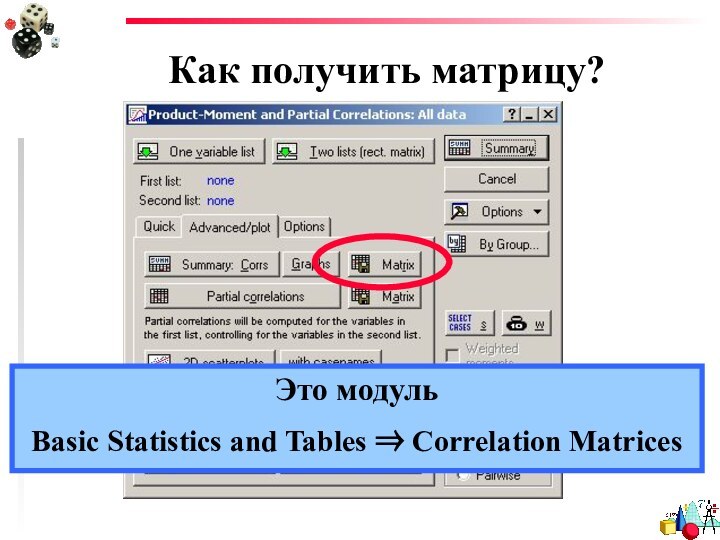
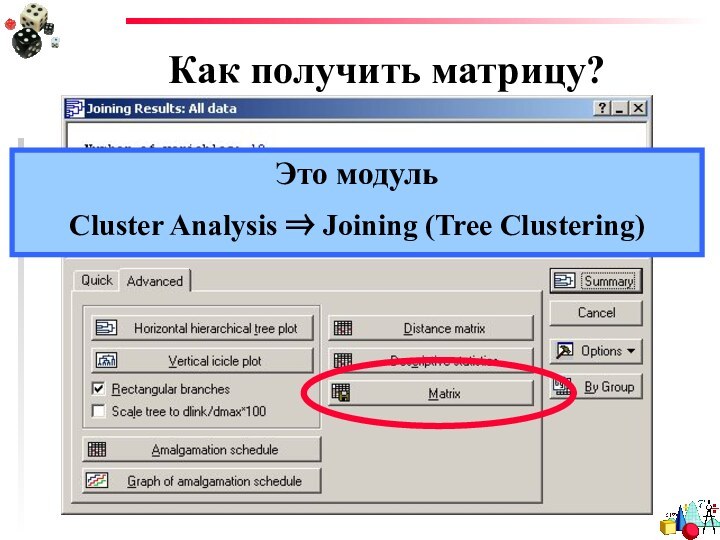
- 16. Как получить матрицу?В модуле, где считают корреляциюВ модуле кластерного анализаСамим посчитать
- 17. Как получить матрицу?Это модуль Basic Statistics and Tables ⇒ Correlation Matrices
- 18. Как получить матрицу?Это модуль Cluster Analysis ⇒ Joining (Tree Clustering)
- 19. Многомерное шкалирование
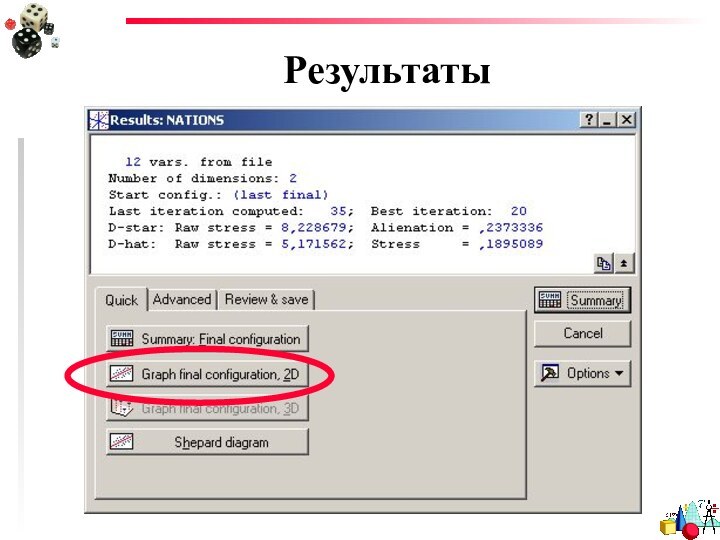
- 20. Результаты
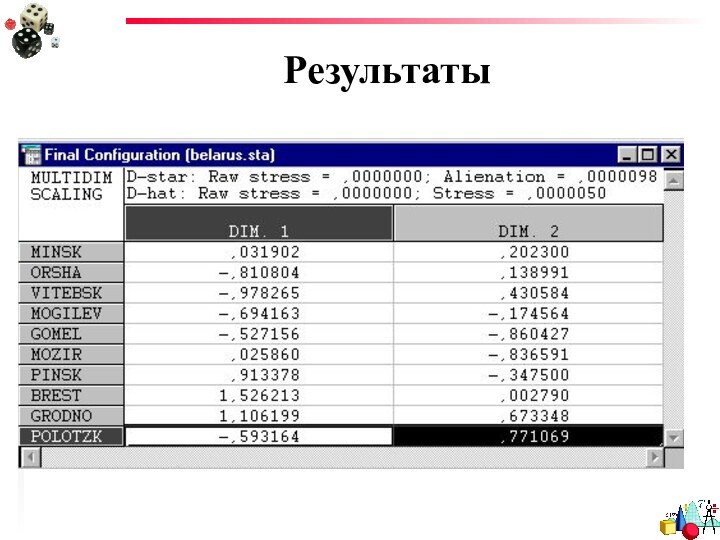
- 21. Результаты
- 22. Результаты
- 23. Ориентация осейОриентация осей может быть выбрана произвольной!
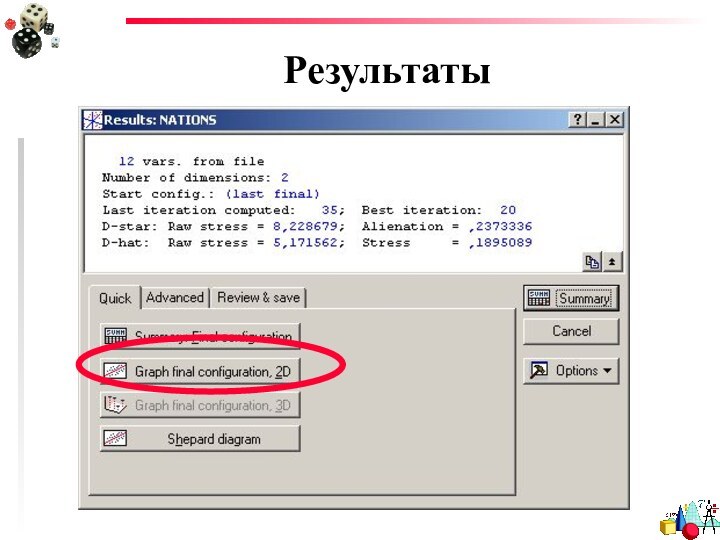
- 24. Результаты
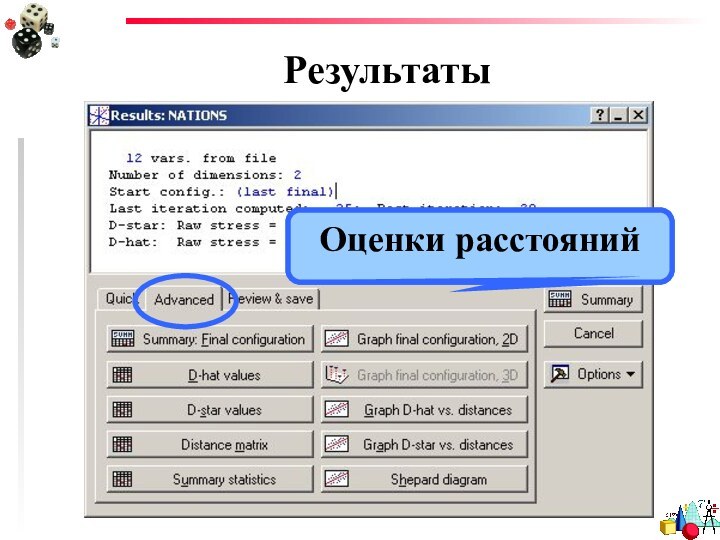
- 25. Результаты
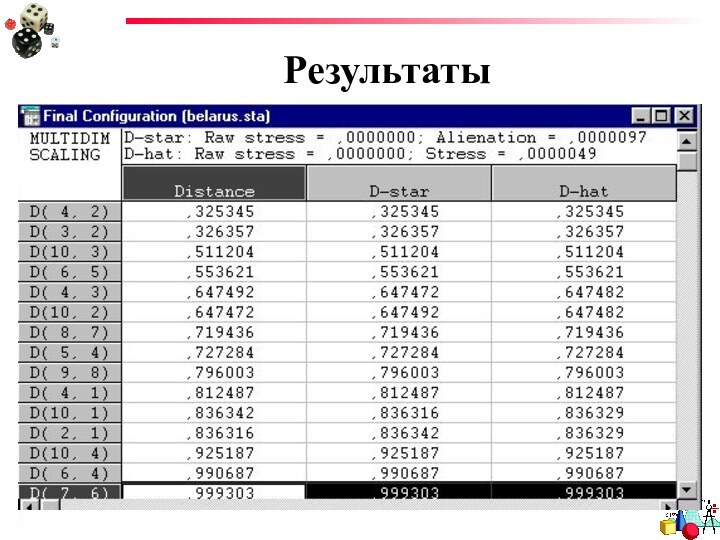
- 26. РезультатыОценки расстояний
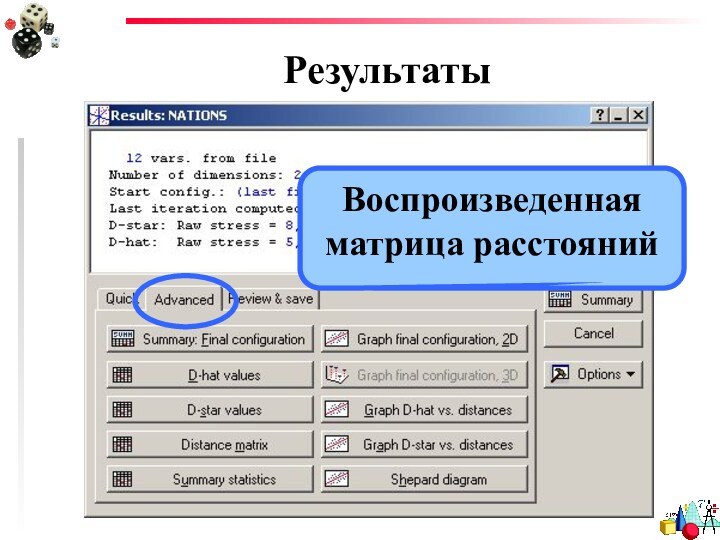
- 27. РезультатыВоспроизведенная матрица расстояний
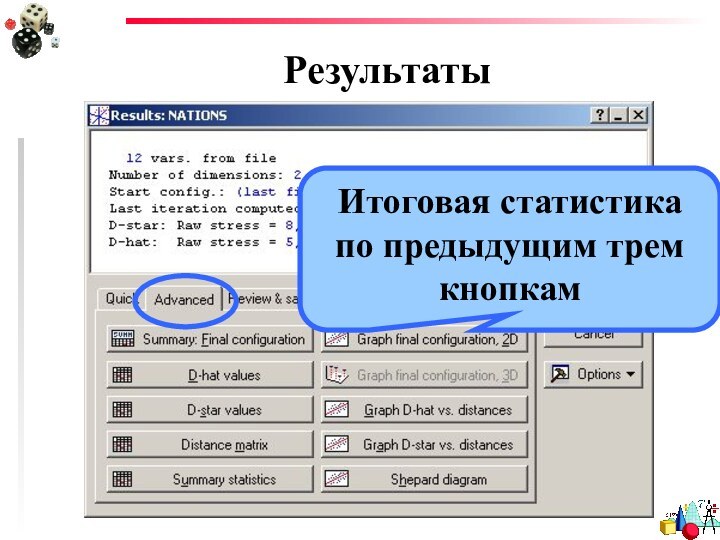
- 28. РезультатыИтоговая статистика по предыдущим трем кнопкам
- 29. Результаты
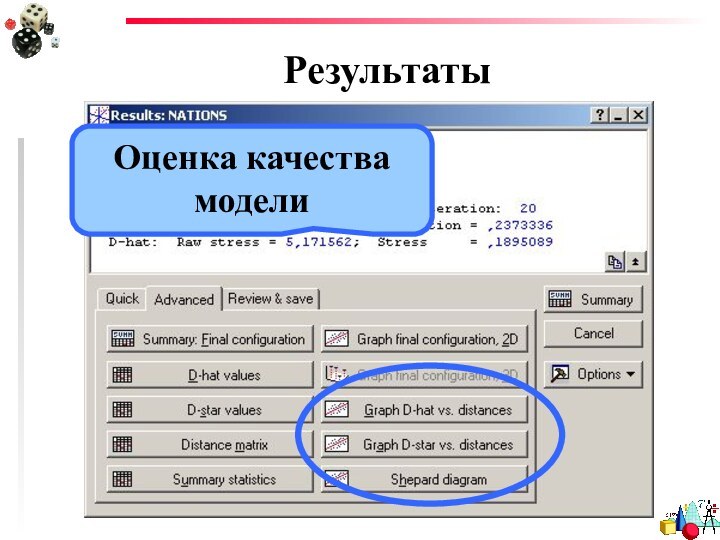
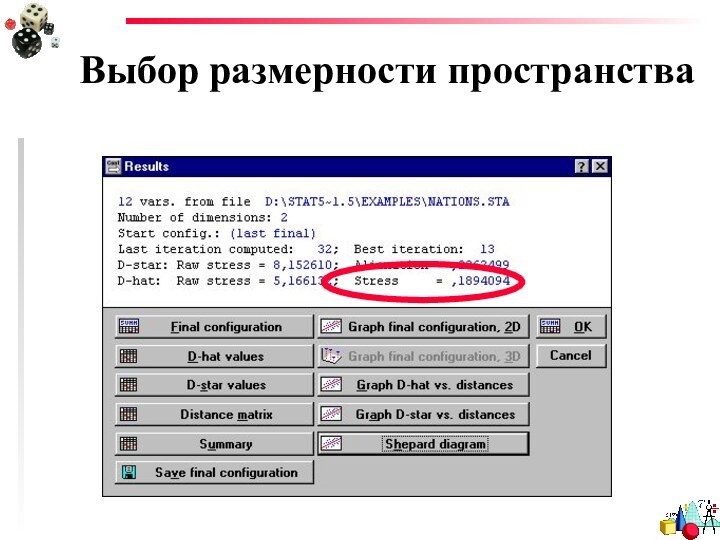
- 30. РезультатыОценка качества модели
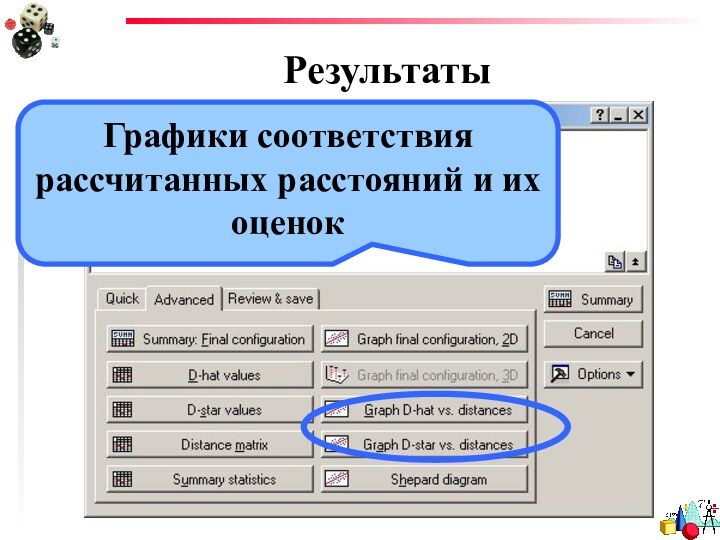
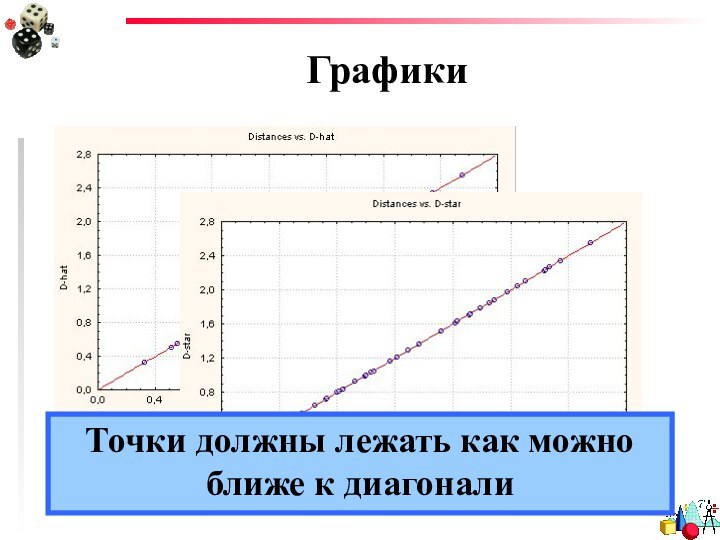
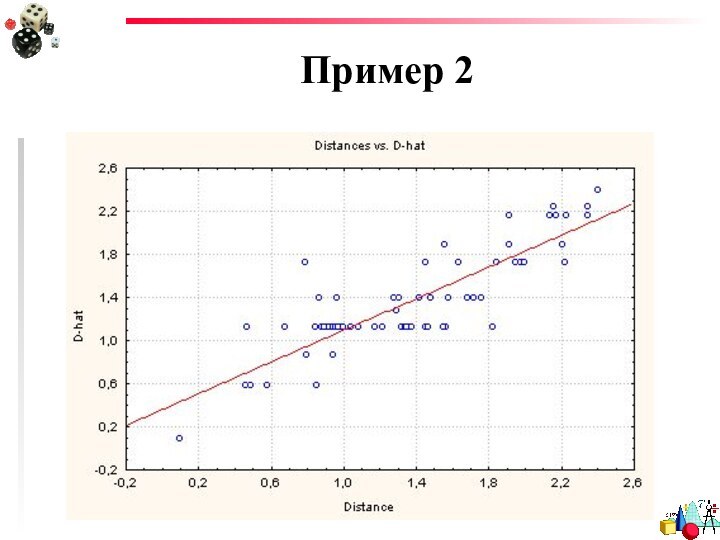
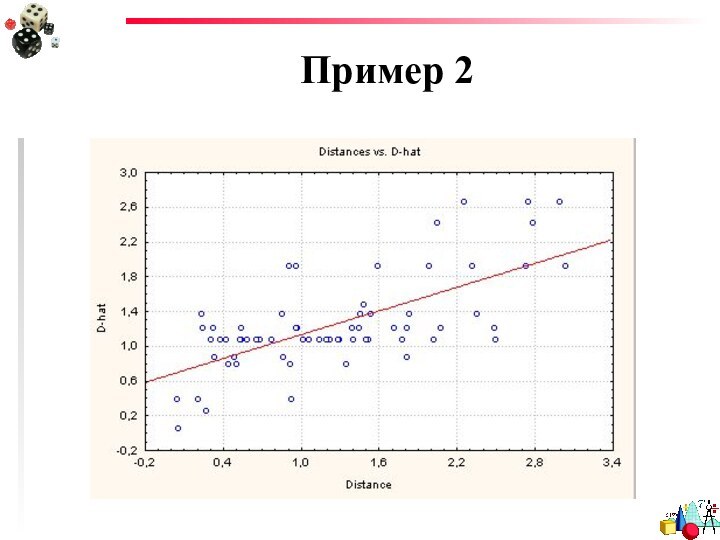
- 31. РезультатыГрафики соответствия рассчитанных расстояний и их оценок
- 32. ГрафикиТочки должны лежать как можно ближе к диагонали
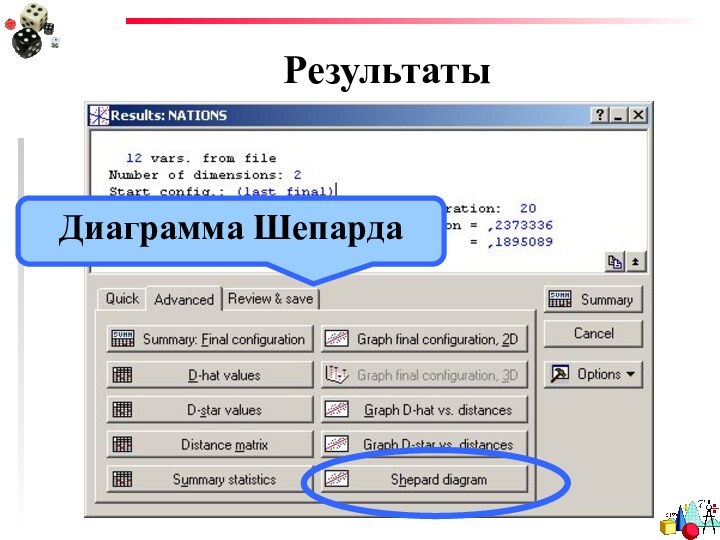
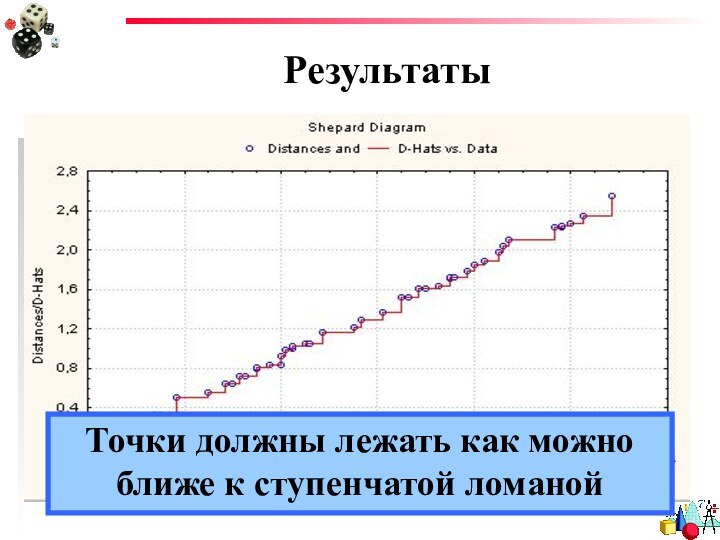
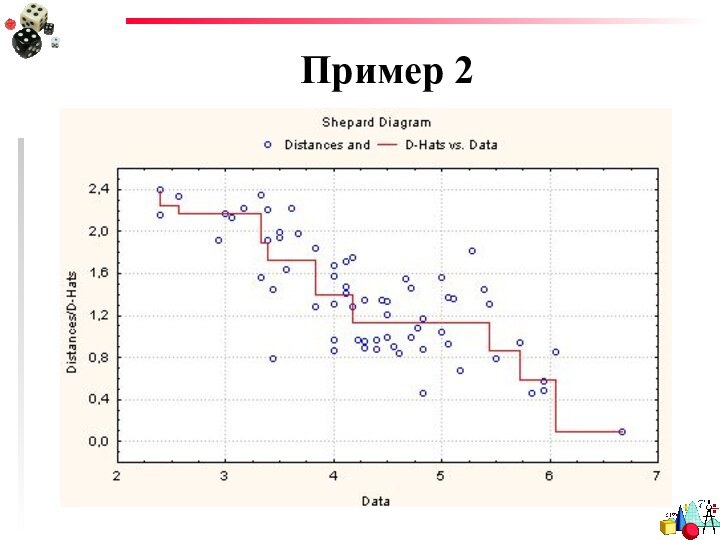
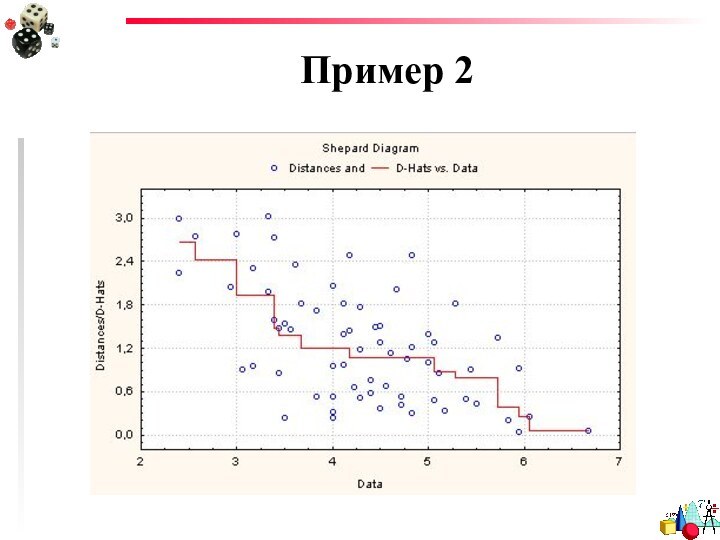
- 33. РезультатыДиаграмма Шепарда
- 34. РезультатыТочки должны лежать как можно ближе к ступенчатой ломаной
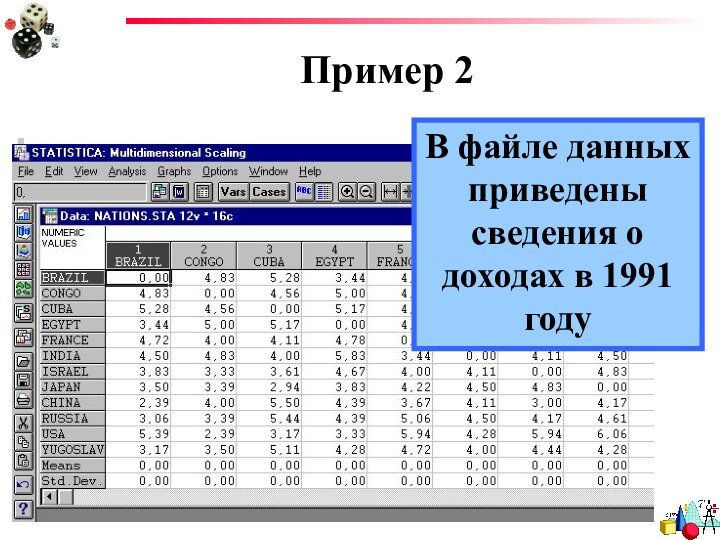
- 35. Пример 2В файле данных приведены сведения о доходах в 1991 году
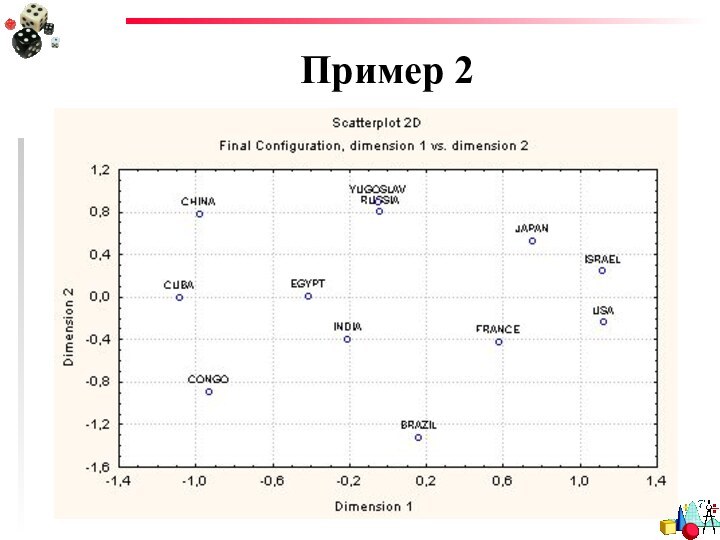
- 36. Пример 2
- 37. Пример 2
- 38. Пример 2
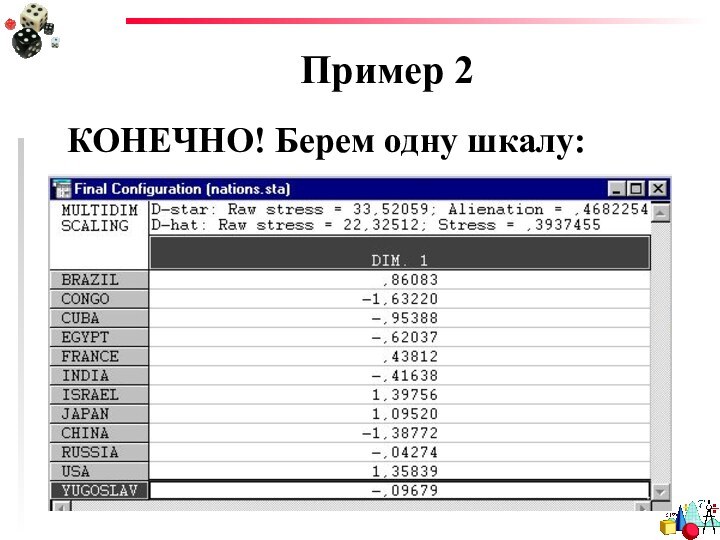
- 39. Пример 2А можно ли попробовать взять другое количество размерностей?
- 40. Пример 2КОНЕЧНО! Берем одну шкалу:
- 41. Пример 2
- 42. Пример 2
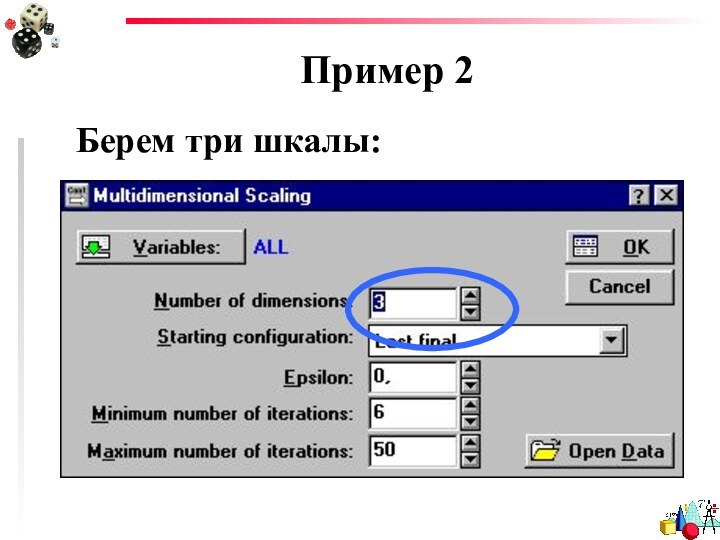
- 43. Пример 2 Берем три шкалы:
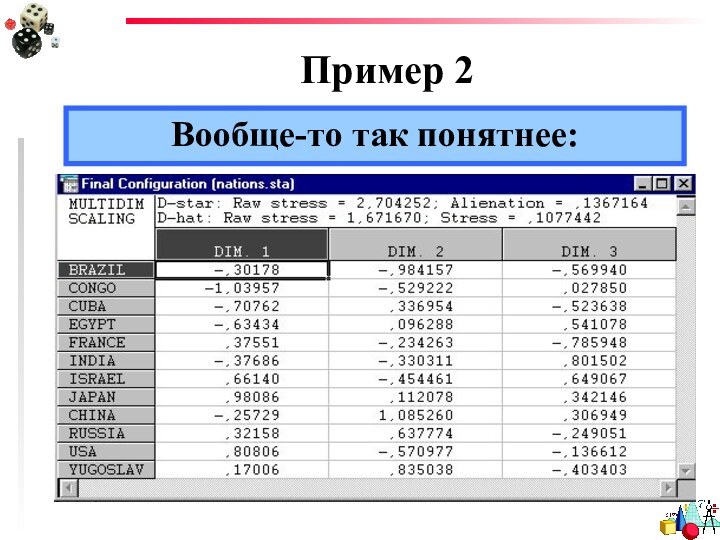
- 44. Пример 2Ну теперь-то все понятно!
- 45. Пример 2Вообще-то так понятнее:
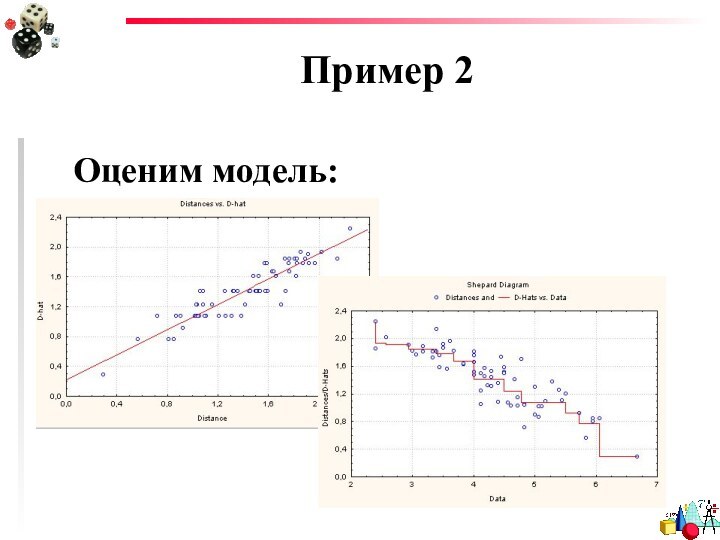
- 46. Пример 2Оценим модель:
- 47. А как вообще выбрать наилучшее количество размерностей?
- 48. Выбор размерности пространстваКритерий каменистой осыпи: на графике зависимости стресса от размерности
- 49. Выбор размерности пространства
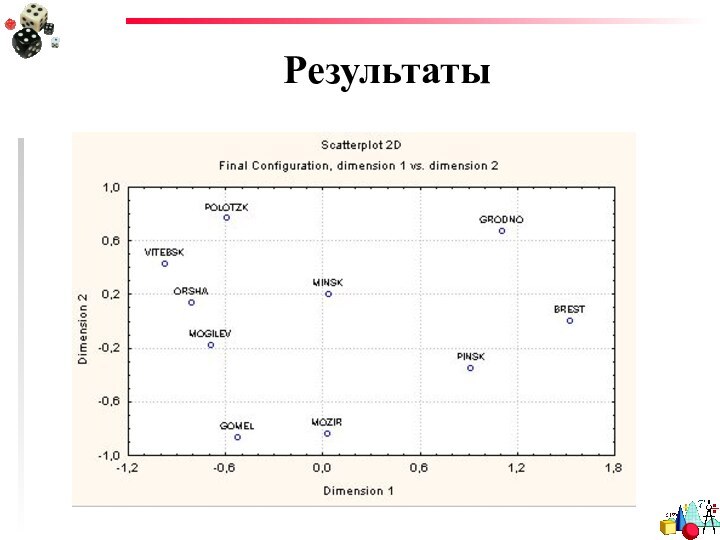
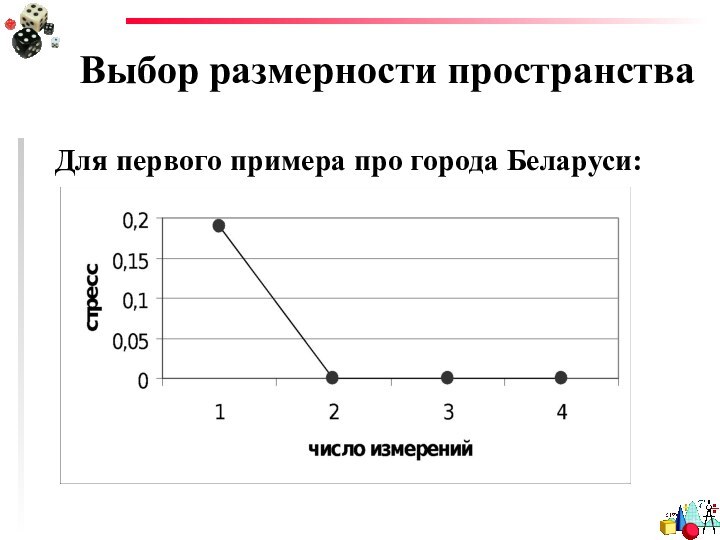
- 50. Выбор размерности пространстваДля первого примера про города Беларуси:
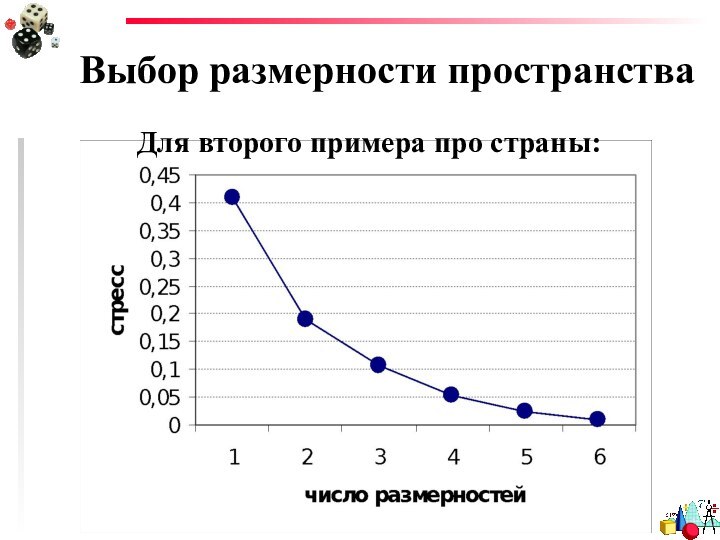
- 51. Выбор размерности пространстваДля второго примера про страны:
- 52. Выбор размерности пространства2 ) Вторым критерием для
- 53. ПреимуществаЧасто информация, полученная от наблюдателя, носит неметрический
- 54. ПреимуществаЭто связано с тем, что информация о
- 55. ПреимуществаВ общем случае, методы МНШ позволяют исследователю
- 56. Полезная литература:К семинару по многомерному шкалированию прочитать:Лосик
- 57. Скачать презентацию
- 58. Похожие презентации
Многомерное шкалированиеМногомерное шкалирование (МШ) можно рассматривать как альтернативу факторному анализу.

























Слайд 2
Многомерное шкалирование
Многомерное шкалирование (МШ) можно рассматривать как альтернативу
факторному анализу.
Слайд 3
Многомерное шкалирование
Целью является поиск и интерпретация «латентных» (т.е.
непосредственно не наблюдаемых) переменных, дающих возможность пользователю объяснить сходства
между объектами, заданными точками в исходном пространстве признаков.
Слайд 4
Многомерное шкалирование
Основная цель:
Выявление структуры исследуемого множества объектов
(структура –
набор основных факторов (шкал), по которым различаются и могут
быть описаны объекты)
Слайд 5
Многомерное шкалирование
Исходная информация для МШ – данные о
различии или близости объектов
Слайд 6
Многомерное шкалирование
В психологии исходными данными для МШ являются
субъективные суждения испытуемых о различии или сходстве стимулов (объектов).
Слайд 7
Многомерное шкалирование
Считается, что в основе таких суждений лежит
ограниченное количество субъективных признаков (критериев), определяющих различение стимулов, и
человек, вынося свои суждения, явно или неявно учитывает эти критерии.
Слайд 8
Многомерное шкалирование
Основная задача МШ:
Реконструкция психологического пространства, заданного небольшим
числом измерений-шкал, и расположение в нем точек-стимулов таким образом,
чтобы расстояние между ними наилучшим образом соответствовали исходным субъективным различиям.
Слайд 9
Многомерное шкалирование
Поэтому
шкала в МШ интерпретируется как критерий,
лежащий в основе различий стимулов.
Слайд 10
Основная идея
Пример: пусть имеется матрица попарных расстояний (т.е.
сходства некоторых признаков) между крупными белорусскими городами. Анализируя матрицу,
стремятся расположить точки с координатами городов в двумерном пространстве (на плоскости), максимально сохранив реальные расстояния между ними.
Слайд 11
Основная идея
В общем случае метод МНШ позволяет таким
образом расположить "объекты" (города в нашем примере) в пространстве
некоторой небольшой размерности (в данном случае она равна двум), чтобы достаточно адекватно воспроизвести наблюдаемые расстояния между ними.
Слайд 12
Основная идея
В результате можно "измерить" эти расстояния
в терминах найденных латентных переменных. Так, в нашем примере
можно объяснить расстояния в терминах пары географических координат Север/Юг и Восток/Запад.
Слайд 13
Многомерное шкалирование
Statistics ⇒ Multivariate Exploratory Techniques ⇒ Multidimensional
Scaling
Слайд 15
Представление данных
Матрица может представлять
1 – корреляцию
2 –
сходство3 – различие
4 –ковариацию
ЭТИ ОБОЗНАЧЕНИЯ ЯВЛЯЮТСЯ СТАНДАРТНЫМИ!





























