- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Множества и операции над ними
Содержание
- 2. Множества и операции над ними Георг Кантор(1845
- 3. Множества a, b, …, x, y, z
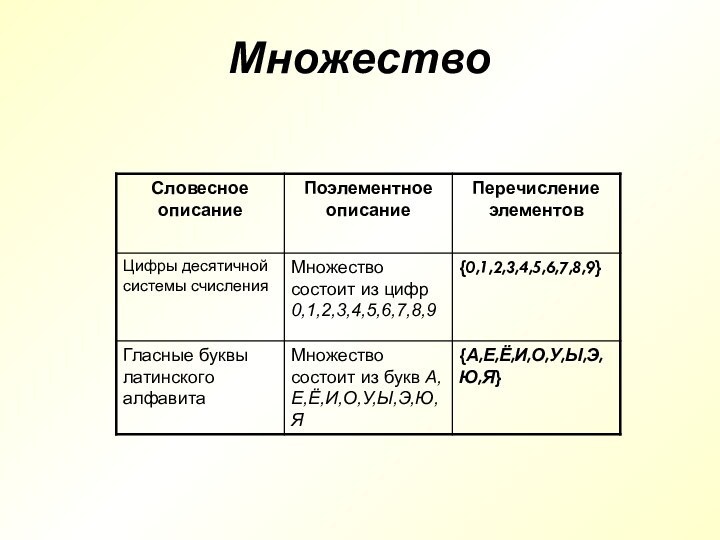
- 4. Множество
- 5. Способы задания множеств
- 6. ПодмножествоЭлементы, образующие множество А, можно объединять не
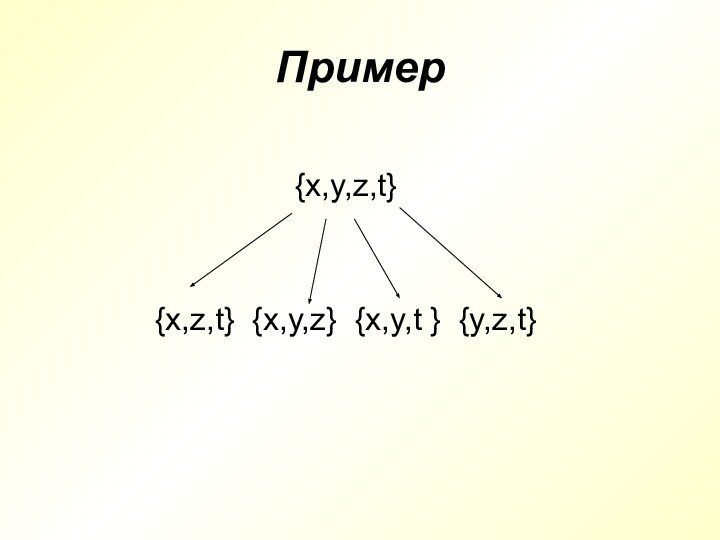
- 7. Пример{x,y,z,t}
- 8. Множество a, b, …, x, y, z
- 9. Пересечение множеств ХYиХ={1;3;5;7;9}Y={3;6;9;12;15}ХY= ?ХY= {3;9}135793691215АВМножество a, b,
- 10. Множество a, b, …, x, y, z
- 11. Скачать презентацию
- 12. Похожие презентации
Множества и операции над ними Георг Кантор(1845 – 1918)«Множество – единое имя для совокупности всех объектов, обладающих данным свойством»
Слайд 3
Множества
a, b, …, x, y, z –
элементы множества
A, B, … X, Y, Z - множества
{
; } – используется для перечисления элементов| - заменяет словосочетание «…таких, что …»
- знак принадлежности, a А
- знак включённости, A B
«Множество – единое имя для совокупности всех
объектов, обладающих данным свойством»
Слайд 6
Подмножество
Элементы, образующие множество А, можно объединять не сразу
все вместе, а группируя их в разных комбинациях.
Если каждый
элемент множества В является элементом множества А, то множество В называют подмножеством множества А.Обозначение: В ϲ А
Слайд 8
Множество
a, b, …, x, y, z –
элементы множества
A, B, … X, Y, Z - множества
- знак принадлежности, a А- знак включённости, A B
{ ; } – используется для перечисления элементов
| - заменяет словосочетание «…таких, что …»
Леонард Эйлер
(1707 – 1783)
А
В
«Множество – единое имя для совокупности всех
объектов, обладающих данным свойством»
Слайд 9
Пересечение множеств
Х
Y
и
Х={1;3;5;7;9}
Y={3;6;9;12;15}
Х
Y
= ?
Х
Y
= {3;9}
1
3
5
7
9
3
6
9
12
15
А
В
Множество
a, b, …,
x, y, z – элементы множества
A, B, … X,
Y, Z - множества - знак принадлежности, a А
- знак включённости, A B
{ ; } – используется для перечисления элементов
| - заменяет словосочетание «…таких, что …»
«Множество – единое имя для совокупности всех
объектов, обладающих данным свойством»
и
Пересечение множеств
Пересечением множеств А и В называют множество,
состоящее из всех общих
элементов множеств А и В
Слайд 10
Множество
a, b, …, x, y, z –
элементы множества
A, B, … X, Y, Z - множества
- знак принадлежности, a А- знак включённости, A B
{ ; } – используется для перечисления элементов
| - заменяет словосочетание «…таких, что …»
и
Пересечение множеств
Пустым множеством
называется множество,
не содержащее
ни одного элемента
М = {1;4;9;…}
N = {2;3}
М N = ?
М N =
1
4
9
2
3
«Множество – единое имя для совокупности всех
объектов, обладающих данным свойством»
Пустое множество
М
N
16
…
