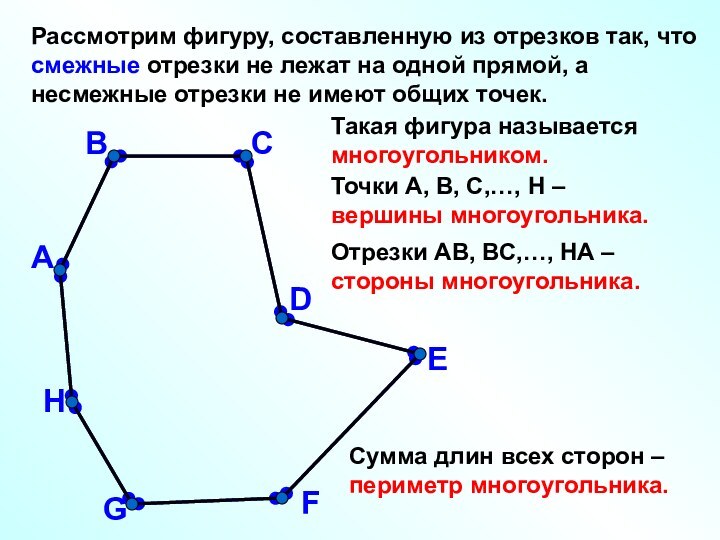
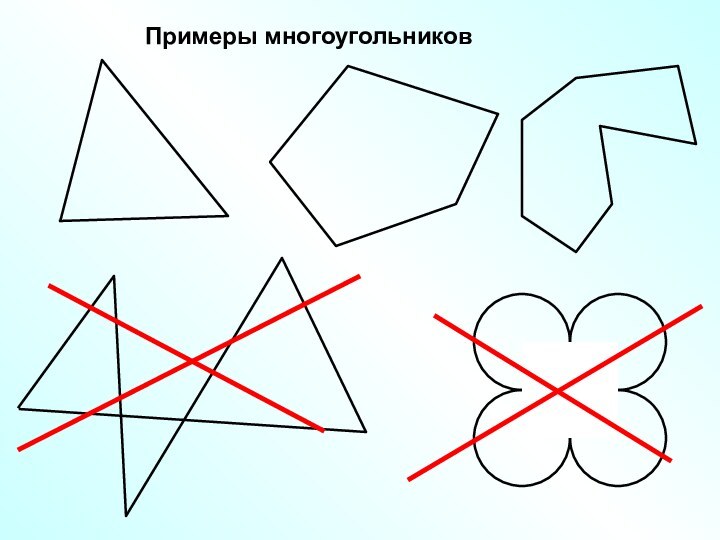
отрезки не лежат на одной прямой, а несмежные отрезки
не имеют общих точек.А
В
С
D
E
F
G
H
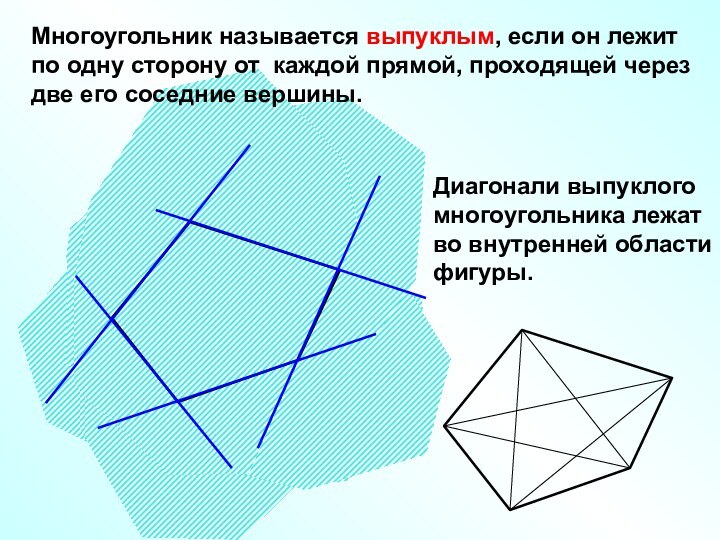
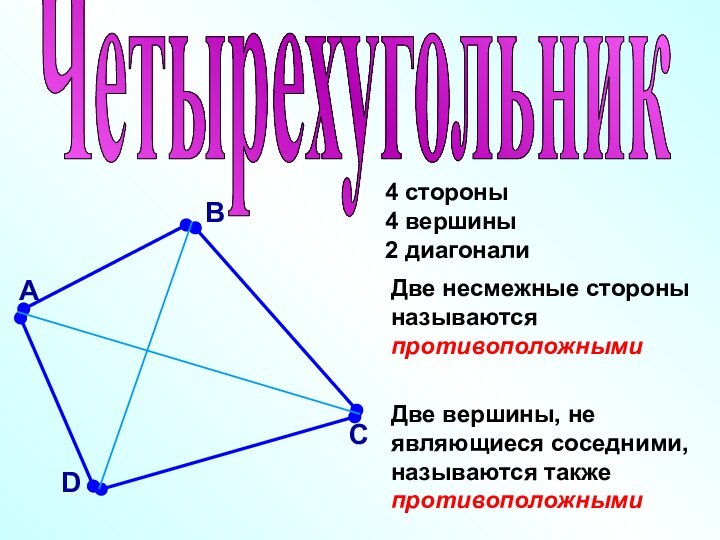
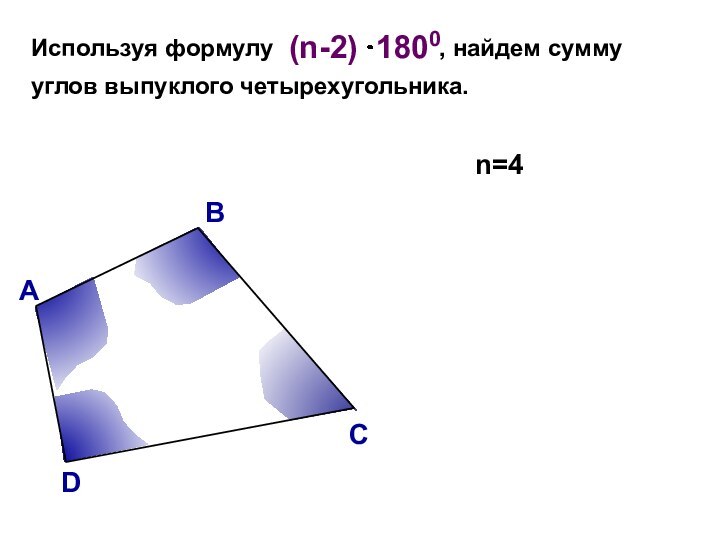
Такая фигура называется многоугольником.
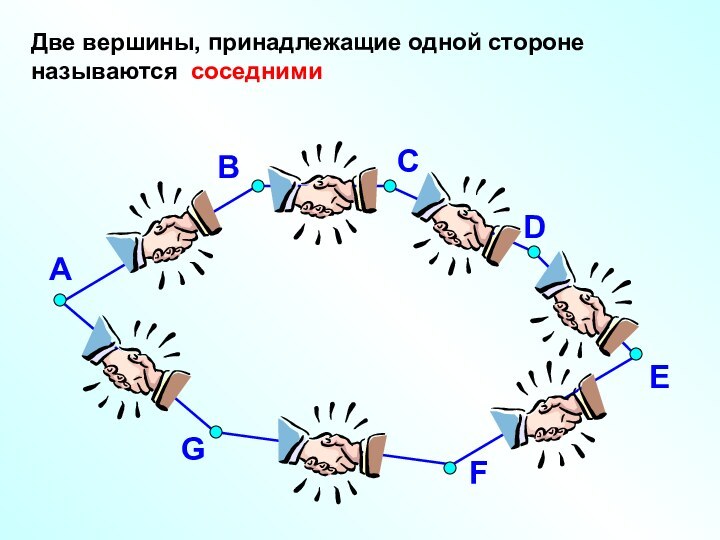
Точки А, В, С,…, H – вершины многоугольника.
Отрезки АВ, ВС,…, HА – стороны многоугольника.
Сумма длин всех сторон – периметр многоугольника.