Презентация на тему Нахождение наибольшего и наименьшего значения функции

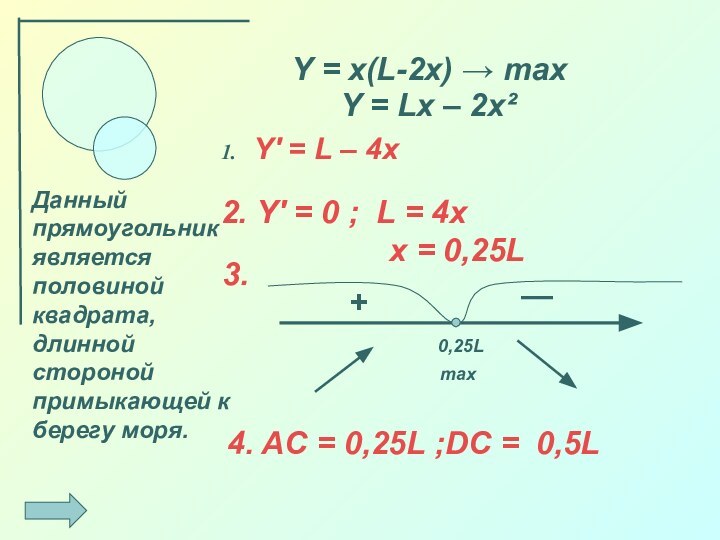
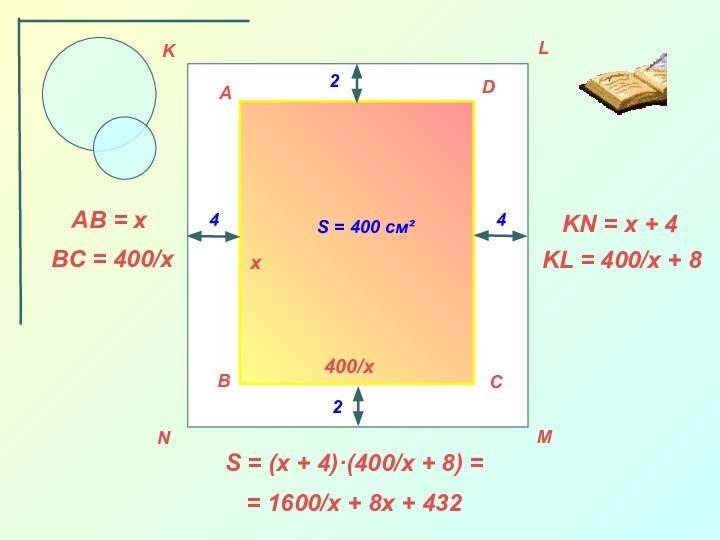
которых производная равна нулю и меняет свой знак.
Вычислить значение

функции в этих точках и на концах отрезка, где определена функция.
Выбрать из полученных значений оптимальное.

Перевести задачу на язык математики, т. е. выразить искомую величину через функцию от некоторой переменной и найти область её определения.

функции.
Найти наибольшее и наименьшее значение функции на отрезке [-1;2]

Y

= N · x² - 2·N · x + 8

корабль пристал к берегу, местные жители согласились продать прибывшим

столько земли, сколько можно огородить её одной бычьей шкурой. Но хитрая царица Дидона разрезала эту шкуру на ремешки, связала их и огородила полученным ремнём большой участок земли, примыкавший к побережью.

Вопрос: какую наибольшую площадь земли могли купить финикийцы?

x(L-2x)

4x

0,25L
+
—
max
Данный прямоугольник является половиной квадрата, длинной стороной примыкающей к

берегу моря.

2. Y′ = 0 ; L = 4x
x = 0,25L

3.

4. AC = 0,25L ;DC = 0,5L

Y = Lx – 2x²

из двух частей: стоимости топлива, пропорциональной кубу скорости баржи,

и стоимости амортизации баржи ( зарплата команды, стоимость оборудования и т. д.). Общая стоимость содержания баржи за час выражается формулой: S = av³ + b, где v- скорость судна в км/ч, a и b – коэффициенты, заданные для каждого судна (для нашего а=0,005, b=40).

Ясно, что расходы на топливо будут тем больше, чем быстрее движется корабль, остальные расходы от скорости не зависят.

Казалось бы, чем медленнее движется корабль, тем дешевле его эксплуатация. Так ли это?

0,005·2v – 40/v²
—
16
+
min


Оптимальная скорость катера для минимальных затрат равна

16 км/ч

2.Y′ = 0 ; 0,01v – 40/v² = 0
0,01v = 40/v²
0,01v³ = 40
v³ = 4000
v ≈ 16 км/ч

3.

страницы книги должен занимать 400 см². Верхние и нижние

поля страницы должны иметь ширину 2 см. Боковые – 4 см.

Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?

= 400/x + 8
KN = x + 4
S =

(x + 4)·(400/x + 8) =
= 1600/x + 8x + 432

min
1. S′ = -1600/x² + 8
2. S′ = 0;

-1600/x² + 8 = 0
1600/x² = 8
x² = 1600/8
x ≈ 14

3.

—

+

min

14

Оптимальные размеры страницы
18х36,5 см.

4. KN = х + 4=18
KL = 400/x + 8≈36,5

в различных сферах деятельности человека.
Д/з решить задачу: Рекламный щит

имеет форму прямоугольника S = 9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром. Определите его стоимость, если суммарная цена материалов и работ по изготовлению за 1 м² составляет 200 грн + 25 грн за погонный метр длины щита.