- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Функции алгебры логики
Содержание
- 2. ПланФункции алгебры логикиЭлементы комбинаторикиЭлементы теории графовТри контрольные работы (в редакторе ТеХ, http://miktex.org/2.8/setup)
- 3. Рекомендуемая литература 1. Журавлёв Ю.И., Флёров Ю.А.
- 4. Функции алгебры логики Джордж Буль (1815-1864)“Математический анализ
- 5. БУЛЬ, ДЖОРДЖ (Boole, George) (1815-1864), английский математик.
- 6. Огастес (Август) де Морган (англ. Augustus de
- 7. Функции алгебры логики. Табличное задание функций.
- 8. Функции алгебры логики.Область определения логических или булевых
- 9. Операции над двумя переменными (двухместные,
- 10. Индуктивное определение формулы:Пусть U - множество переменных.
- 11. Определение. Функция от n переменных определенная на
- 12. «Табличное» задание функции
- 13. Алгебраические свойства элементарных операций 1. Коммутативность (или
- 14. 2. Ассоциативность операции означает, что
- 15. 3. Дистрибутивность (распределительный закон) операции относительно
- 16. Дистрибутивность импликации:
- 17. 4. Имеет место следующее соотношение для двойного отрицания:
- 18. 5. Имеют место следующие соотношения между отрицанием,
- 19. 6. Имеют место следующие соотношения, связанные с
- 20. 7. Константы могут быть выражены следующим образом:
- 21. 8. Правила поглощения:
- 22. 9. Выполняются следующие свойства конъюнкции и дизъюнкции:
- 23. Все указанные тождества могут быть проверены путем
- 24. Определение. Через P2(n) будем обозначать множество всех
- 25. Переменная xi (1 i n) функции
- 26. 8. Правила поглощения:
- 27. Разложение функций алгебры логики по переменным Чтобы
- 28. Легко видеть, что x = 1 тогда
- 29. Лемма. (О разложении функции по одной переменной).
- 30. Доказательство. Отметим прежде всего, что представление
- 31. Лемма 2.3. Конъюнкция (произведение)
- 32. В дальнейшем будем употреблять следующие обозначения:
- 33. Теорема 2.4. (О разложении функции по нескольким
- 34. Доказательство. Рассмотрим произвольный набор значений переменных (1,
- 35. Представление (2.2) называется дизъюнктивным разложением функции по
- 36. Выпишем такое разложение для конкретной функции трех переменных по переменным x2 и x3:
- 37. Если k = n , то получаем
- 38. Итак, в этом случае разложение имеет вид:Это
- 39. Теорема 2.5. Произвольную функцию алгебры логики можно
- 40. Доказательство.1. Пусть f(x1, ... , xn) =
- 41. Любую булеву функцию можно выразить формулой над
- 42. Пример. Построить совершенную ДНФ для функции, заданной таблицей:Имеем:
- 43. Задача выполнимости булевых формул (SAT или ВЫП)
- 44. Чтобы четко сформулировать задачу распознавания, необходимо условиться
- 45. Вычислительная сложностьВ 1971-м году в статье Стивена
- 46. Две задачи
- 51. Функциональная полнота систем функций алгебры логики
- 52. 1. Замена переменных.Пусть f(x1, x2, ... ,
- 53. Пример. Пусть имеется функция Тогда при замене переменных из функции можно получить функцию .
- 54. 2. Суперпозиция функций алгебры логики. Пусть имеется
- 55. Пример.Пусть задано множество функций F =
- 56. Система функций называется полной, если при помощи
- 57. Мы уже имеем некоторый набор полных систем:{x+y,
- 58. Замкнутые классы. Множество (класс) K функций алгебры
- 59. Примеры. {0}, {1} - замкнутые классы. Множество
- 60. Замкнутые классы. 1. Т0 - класс функций,
- 61. Поскольку таблица для функции f из класса
- 63. 2. T1 - класс функций, сохраняющих 1.f(1,
- 64. Т1 - замкнутый класс
- 65. 3. L - класс линейных функций.0, 1,
- 66. Докажем, что xy L .Предположим противное.
- 67. Поскольку линейная функция однозначно определяется заданием значений
- 68. 4. S - класс самодвойственных функций.Функция
- 69. 0* = 1,1* = 0,x* = x,(x1
- 70. Теорема. Если функция получена как суперпозиция
- 71. Доказательство.φ*(x1 ,..., xn) = f(x1 ,..., xn) =
- 72. Обозначим через S класс всех самодвойственных функций
- 73. На наборах
- 74. Докажем теперь, что класс S замкнут. Так
- 75. Пусть
- 76. 5. М - класс монотонных функций.Набор
- 78. Функция алгебры логики называется монотонной, если для
- 79. 0, 1, x, xy, xy M;x+y,
- 80. Скачать презентацию
- 81. Похожие презентации






































































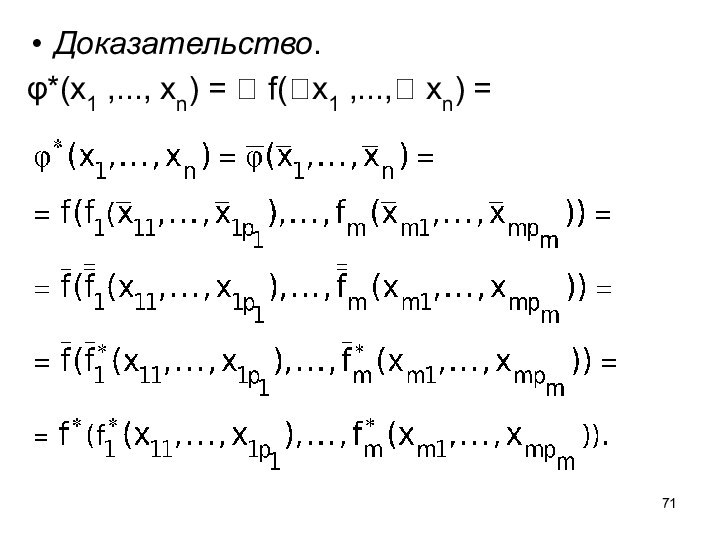







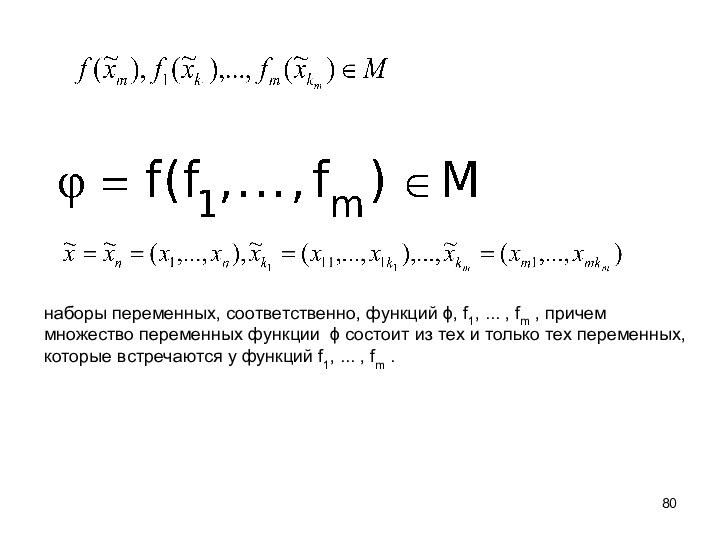
Слайд 2
План
Функции алгебры логики
Элементы комбинаторики
Элементы теории графов
Три контрольные работы
(в редакторе ТеХ, http://miktex.org/2.8/setup)
Слайд 3
Рекомендуемая литература
1. Журавлёв Ю.И., Флёров Ю.А. Дискретный анализ.
Часть I: Учебное пособие. – М.: МФТИ, 1999.
2. Стэнли
Р. Перечислительная комбинаторика. -М.: Мир, 1990.3. Липский В. Комбинаторика для программистов. - М.: Мир, 1988.
4. Рыбников К.А. Введение в комбинаторный анализ. - М.: МГУ,1985.
5. Гаврилов Г.И., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. -М.: Наука, 1992.
6. Риордан Дж. Введение в комбинаторный анализ. - М.: ИЛ, 1963.
7. Холл М. Комбинаторика. - М.: Мир, 1970.
8. Мендельсон Э. Введение в математическую логику.- М.: Наука, 1976.
9. Дискретная математика и математические вопросы кибернетики/
Под ред. С.В.Яблонского, О.В.Лупанова, Т.1, -М.; Наука, 1974.
10. Яблонский С.В. Введение в дискретную математику. -М.: Наука, 1986.
11. Оре О. Теория графов. - М.: Наука, 1968.
12. Кристофидис Н. Теория графов. Алгоритмический подход. -М.: Мир, 1987.
13. Емеличев В.А., Мельников О.И. и др. Лекции по теории графов. М.: Наука, 1990.
14. Уилсон Р.Дж. Введение в теорию графов. - М.: Мир, 1977.
15. Харари Ф. Теория графов. - М.: Мир,1973.
16. Журавлёв Ю.И., Флёров А.А., Федько О.С., Дадашев Т.М. Сборник задач по дискретному анализу. – М.: МФТИ, 2000.
17. Гжегорчик А. Популярная логика.- М.: Наука, 1979.
18. Леонтьев В.К. Избранные задачи комбинаторного анализа. – М. Изд-во МГТУ им. Н.Э. Баумана, 2001.
19. Лазарев А.А. Теория расписаний. Оценки абсолютной погрешности и схема приближённого решения задач теории расписаний: Учебное пособие. – М.: МФТИ, 2008.
20. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир. – 1982.
21. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ. – М. – 2005. 1293 с.
Слайд 4
Функции алгебры логики
Джордж Буль (1815-1864)
“Математический анализ логики, являющийся
очерком, касающимся исчисления дедуктивных рассуждений”, (1847 г.),
“Исследования законов мысли.
на которых основываются математические теории логики и вероятностей”, (1854 г.).Аугустус (Огастес, Август) де Морган (1806-1871)
“Формальная логика или исчисление выводов, необходимых и возможных” (1847 г.).
Слайд 5
БУЛЬ, ДЖОРДЖ (Boole, George) (1815-1864), английский математик. Родился
2 ноября 1815 в Линкольне. В возрасте 16 лет стал помощником учителя частной школы
в Донкастере, в 1835 открыл собственную школу в Линкольне. В свободное время читал математические журналы, работы И.Ньютона, П.Лапласа и Ж.-Л.Лагранжа, начал вести самостоятельные алгебраические исследования. В 1839 написал первую научную работу Исследования по теории аналитических преобразований (Researches on the Theory of Analytical Transformations), которая была опубликована "Кембриджским математическим журналом" ("Cambridge Mathematical Journal"). В 1844 появилась его первая работа, где высказывалась идея объединения алгебры и логики, а в 1847 вышла в свет статья Математический анализ логики (The Mathematical Analysis of Logic), которая положила начало созданию "алгебры высказываний", получившей впоследствии название булевой алгебры. Благодаря этой публикации Буль в 1849 был назначен профессором математики Куинз-колледжа (Корк, Ирландия), где преподавал до конца жизни. В 1857 был избран членом Лондонского королевского общества. Основные идеи Буля суммированы в его работе Исследование законов мышления, на которых основаны математические теории логики и вероятностей (An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities, 1854). Здесь впервые определено в явном виде исчисление классов (или множеств), введено обозначение для их пересечения, объединения и т.д., показано, что исчисление классов можно интерпретировать как исчисление высказываний. Булевы алгебры — особые алгебраические системы, для которых определены две операции, — нашли широкое применение в различных разделах математики: в теории вероятностей, топологии, функциональном анализе, а также в создании вычислительных машин. Умер Буль в Баллинтемпле (графство Корк, Ирландия) 8 декабря 1864.Слайд 6 Огастес (Август) де Морган (англ. Augustus de Morgan,
27 июня 1806), Мадура, Индия — 8 марта 1871, Лондон) —
шотландский математик и логик; профессор математики университетского колледжа в Лондоне (1828—1831, 1836—1866); первый президент (1866) Лондонского математического общества.Основные труды: по математической логике и теории рядов; к своим идеям в алгебре логики пришёл независимо от Дж. Буля; изложил (1847) элементы логики высказываний и логики классов, дал первую развитую систему алгебры отношений; с его именем связаны известные теоретико-множественные соотношения (законы де Моргана).
Слайд 7 Функции алгебры логики. Табличное задание функций. Элементарные
функции, их свойства, таблица операций, коммутативность, ассоциативность, дистрибутивность элементарных
функций.Формулы и функции алгебры логики. Теоремы о разложении функций по одной и нескольким переменным. Совершенная дизъюнктивная нормальная форма. Задача о ВЫПОЛНИМОСТИ. Определение понятия NP-трудности задач.
Функциональная полнота систем функций алгебры логики. Замкнутые классы. Пять предполных замкнутых классов T0, T1, L, S, M. Пересечение данных классов. Теорема о функции двойственной к суперпозиции. Критерий функциональной полноты систем функций алгебры логики (теорема Поста). Примеры полных систем функций алгебры логики. Основная лемма. Лемма о несамодвойственной функции. Лемма о немонотонной функции. Лемма о нелинейной функции. Следствия из критерия полноты.
Слайд 8
Функции алгебры логики.
Область определения логических или булевых переменных
0 и 1
Область значений функций также 0 и 1
Функция
от одной переменной f(x)x f(x)
0 0 0 1 1
1 0 1 0 1
0 x x 1
Слайд 9
Операции над двумя переменными (двухместные, бинарные операции)
x
y x y x y xy xy
x+y x|y xy0 0 0 0 1 1 0 1 1
0 1 0 1 1 0 1 1 0
0 0 1 0 0 1 1 0
1 1 1 1 1 1 0 0 0
2n конъюнкция & и min(x,y) дизъюнкция max (x,y) импликация эквивалентность сумма по модулю 2 +
штрих (Шеффера) | “не x или не y” стрелка (Пирса) “не x и не y”.
Слайд 10
Индуктивное определение формулы:
Пусть U - множество переменных. Тогда
множество формул алгебры логики над U определяется следующим образом:
1.
Всякая переменная - формула. 2. Константы 0 и 1 - формулы.
3. Если А - формула, то А (или в другой записи ) - формула.
4. Если А и В - формулы, то (АВ), (АВ), (АВ), (А+В), (АВ), (АВ), (АВ) - формулы.
5. Формулами являются те и только те выражения, которые могут быть получены из констант, переменных и логических связок за конечное число шагов 1- 4.
Слайд 11
Определение. Функция от n переменных
определенная на множестве
и
принимающая значения из множества {0, 1}, называется функцией алгебры
логики или булевой функцией.F(x1 ,x2 ,x3,…, xn),
Слайд 12
«Табличное» задание функции
x1 x2 ... xn-1 xn f(x1, x2, ...
xn-1, xn)0 0 ... 0 0 f(0, 0, ... , 0, 0)
0 0 ... 0 1 f(0, 0, ... , 0, 1)
0 0 ... 1 0 f(0, 0, ... , 1, 0)
......................
1 1 ... 1 1 f(1, 1, ... , 1, 1)
2n
Слайд 13
Алгебраические свойства элементарных операций
1. Коммутативность (или перестановочность) операции
означает, что
. Логическая операция коммутативна, если связка принадлежит следующему множеству связок (существенно только, чтобы символ в равенстве всюду имел один и тот же смысл):Слайд 14 2. Ассоциативность операции означает, что
.Свойство
ассоциативности позволяет записывать формулы, содержащие одинаковые ассоциативные связки, без скобок, например, .Логическая операция ассоциативна, если связка принадлежит следующему множеству связок (существенно только, чтобы символ в равенстве всюду имел один и тот же смысл):
.
Слайд 15 3. Дистрибутивность (распределительный закон) операции относительно операции
означает, что
.Дистрибутивность конъюнкции:
- дистрибутивность конъюнкции относительно дизъюнкции;
- дистрибутивность конъюнкции относительно суммы по модулю 2.
Дистрибутивность дизъюнкции:
- дистрибутивность дизъюнкции относительно конъюнкции;
- дистрибутивность дизъюнкции относительно импликации;
- дистрибутивность дизъюнкции относительно эквивалентности.
Слайд 16
Дистрибутивность импликации:
- дистрибутивность импликации относительно конъюнкции;
- дистрибутивность импликации относительно дизъюнкции;
- дистрибутивность импликации относительно импликации.
Слайд 18 5. Имеют место следующие соотношения между отрицанием, конъюнкцией
и дизъюнкцией:
закон
(правила) де Моргана.Указанные соотношения отражают отношение двойственности между дизъюнкцией и конъюнкцией.
Слайд 19 6. Имеют место следующие соотношения, связанные с “навешиванием
отрицания” на элементарные логические функции:
Слайд 23 Все указанные тождества могут быть проверены путем сопоставления
функций, реализуемых правой и левой частями формул, сопоставление таблиц
значений функций.Все элементарные функции могут быть выражены через одну-единственную: штрих Шеффера или стрелку Пирса.
Слайд 24 Определение. Через P2(n) будем обозначать множество всех разных
булевых функций размерности n.
Теорема. Число p2(n) всех функций из
P2(n), зависящих от переменных x1, x2, ... , xn , равно .Слайд 25 Переменная xi (1 i n) функции f(x1,
x2, ... ,xi-1, xi , xi+1, ... , xn
) из P2(n)называется существенной, если можно указать такие наборыи
значений переменных, что
В противном случае переменную xi называют несущественной или фиктивной переменной функции f.
Две функции f(x1, x2, ... ,xi-1, xi , xi+1, ... , xn ) и
g(x1, x2, ... ,xi-1, xi , xi+1, ... , xn )
называются равными, если множества их существенных переменных совпадают и на любых двух наборах
(x1, x2, ... ,xi-1, xi , xi+1, ... , xn ) и
(y1, y2, ... ,yi-1, yi , yi+1, ... , yn ),
различающихся быть может только значениями несущественных переменных, значения функций одинаковы: f(x)=g(y).
Если f(x) и g(y) - равные функции, то одну из них можно получить из другой путем добавления и/или изъятия несущественных переменных.
Слайд 27
Разложение функций алгебры логики по переменным
Чтобы иметь возможность
единообразно записывать переменные с отрицанием и без отрицания введем
следующее обозначение:Слайд 28 Легко видеть, что x = 1 тогда и
только тогда, когда x = , то есть значение
“основания” равно значению “показателя”.Слайд 29 Лемма. (О разложении функции по одной переменной). Пусть
f(x1 , ... , xn) - произвольная функция алгебры
логики, тогда справедливо следующее представление f в форме разложения по переменной x1 : (2.1)
Слайд 30 Доказательство. Отметим прежде всего, что представление (2.1),
естественно, справедливо для произвольной переменной xi из множества переменных
функции f. Для доказательства рассмотрим произвольный набор значений переменных (1, ... , n) и покажем, что левая и правая части соотношения (2.1) принимают на нем одно и то же значение.Рассмотрим набор значений переменных (1, 2, ... , n). Левая часть (2.1) принимает на этом наборе значение f(1, 2 ,..., n ), а правая часть - значение
1f(1, 2, ... , n ) 0f(0, 2, ... , n ) = f (1, 2, ... , n ).
Таким образом, на наборах (1, 2, ... , n) левая и правая части (2.1) принимают одинаковые значения.
Рассмотрим набор значений переменных (0, 2, ... , n). Левая часть (2.1) принимает на этом наборе значение f(0, 2 ,..., n ), а правая часть - значение
0f(1, 2, ... , n ) 1f (0, 2, ... , n ) = f (0, 2, ... , n ).
Таким образом, на наборах (0, 2, ... , n) левая и правая части (2.1) принимают одинаковые значения.
Тем самым мы доказали, что левая и правая части соотношения (2.1) принимают одинаковые значения на всех наборах (1, ... , n).
Слайд 31
Лемма 2.3. Конъюнкция (произведение)
тогда и только
тогда, когда.
Доказательство. Произведение (конъюнкция) равно 1 тогда и только тогда, когда каждый сомножитель равен 1, но x = 1 тогда и только тогда, когда x = .
Слайд 33 Теорема 2.4. (О разложении функции по нескольким переменным). Пусть
f(x1 , ... , xn) - произвольная функция алгебры
логики. Тогда ее можно представить в следующей форме:(2.2)
Слайд 34 Доказательство. Рассмотрим произвольный набор значений переменных (1, ...
, n) и покажем, что левая и правая части
соотношения (2.2) принимают на нем одно и то же значение. Левая часть даетf(1 ,..., k , k+1 ,..., n).
Правая часть дает
Слайд 35 Представление (2.2) называется дизъюнктивным разложением функции по
k переменным.
Пример. Для k = 2 разложение в
дизъюнктивную форму имеет вид:Слайд 37 Если k = n , то получаем разложение
Оно может быть преобразовано при f(x1, ... , xn)
0 следующим образом:
Слайд 38
Итак, в этом случае разложение имеет вид:
Это разложение
называется совершенной дизъюнктивной нормальной формой (совершенная ДНФ.). Оно определено
для любой функции f, не равной константе 0.Слайд 39 Теорема 2.5. Произвольную функцию алгебры логики можно выразить
формулой при помощи операций , , , причем операция
применяется только к переменным
Слайд 40
Доказательство.
1. Пусть f(x1, ... , xn) = 0.
Тогда, очевидно,
f(x1, ... , xn) = x1
x1 .2. Пусть f(x1, ... , xn) 0. Представим ее в форме совершенной ДНФ:
Таким образом, в обоих случаях функция f выражается в виде формулы через конъюнкцию, дизъюнкцию и отрицание, причем отрицание применяется только к символам переменных.
Слайд 41 Любую булеву функцию можно выразить формулой над множеством
операций
{, , }, состоящим из
трех функций: отрицания, конъюнкции и дизъюнкции. Данная теорема носит конструктивный характер, так как она позволяет для каждой функции построить реализующую ее формулу (совершенную ДНФ). А именно, берем таблицу для функции f(x1, ... , xn) (f 0) и отмечаем в ней все строки (1, ... , n), в которых f(1, ... , n) =1, для каждой такой строки образуем логическое произведение а затем соединяем все полученные конъюнкции знаком дизъюнкции.
Слайд 43 Задача выполнимости булевых формул (SAT или ВЫП) —
задача распознавания, важная для теории вычислительной сложности.
Экземпляром задачи SAT
является булева формула, состоящая только из имен переменных, скобок и операций (И), (ИЛИ) и (HE). Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ЛОЖЬ и ИСТИНА так, чтобы формула стала истинной.Согласно теореме Кука, доказанной Стивеном Куком в 1971-м году, задача SAT NP-полна.
Слайд 44 Чтобы четко сформулировать задачу распознавания, необходимо условиться об
алфавите, с помощью которого задаются экземпляры языка. Этот алфавит
должен быть фиксирован и конечен. Обычно используют следующий алфавит:{ , , , (, ), x, 0, 1}.
При использовании такого алфавита скобки и операторы записываются естественным образом, а переменные получают следующие имена: x1, x10, x11, x100 и т. д., согласно их номерам, записанным в двоичной системе счисления.
Пусть некоторая булева формула, записанная в обычной математической нотации, имела длину N символов. В ней каждое вхождение каждой переменной было описано хотя бы одним символом, следовательно, всего в данной формуле не более N переменных. Значит, в предложенной выше нотации каждая переменная будет записана с помощью символов. В таком случае, вся формула в новой нотации будет иметь длину символов, то есть длина строки возрастет в полиномиальное число раз.
Например, формула
примет вид
Слайд 45
Вычислительная сложность
В 1971-м году в статье Стивена Кука
был впервые введен термин «NP-полная задача», и задача SAT
была первой задачей, для которой доказывалось это свойство.В доказательстве теоремы Кука каждая задача из класса NP в явном виде сводится к SAT. После появления результатов Кука была доказана NP-полнота для множества других задач. При этом чаще всего для доказательства NP-полноты некоторой задачи приводится полиномиальное сведение задачи SAT к данной задаче, возможно в несколько шагов, то есть с использованием нескольких промежуточных задач.
Слайд 51
Функциональная полнота систем функций алгебры
логики
Выше мы видели,
что всякая функция алгебры логики может быть выражена в
виде формулы через элементарные функции , xy, xy. В связи с этим возникает вопрос, какими свойствами должна обладать система функций, чтобы через функции этой системы можно было выразить произвольную функцию алгебры логики?Новые функции получаются из имеющихся в заданной системе функций с помощью операций замены переменных и суперпозиции. Опишем эти две операции.
Слайд 52
1. Замена переменных.
Пусть f(x1, x2, ... , xn)
- заданная функция алгебры логики. Будем говорить, что функция
(y1, y2, ... , yn) получена операцией замены переменных из функции f(x1, x2, ... , xn), если осуществлена подстановка переменных
Слайд 53
Пример. Пусть имеется функция
Тогда при замене переменных
из функции
можно получить функцию
.
Слайд 54
2. Суперпозиция функций алгебры логики.
Пусть имеется функция
f(x1, x2, ... , xn) и функции
,тогда функцию
будем называть суперпозицией функции f(x1, x2, ... , xn) и функций .
Другими словами: пусть F = { fj } - набор функций алгебры логики, не обязательно конечный. Функция f называется суперпозицией функций из множества F или функцией над F, если она получена из функции
путем замены одной или нескольких ее переменных функциями из множества F.
Слайд 55
Пример.
Пусть задано множество функций
F =
{f1(x1), f2 (x1 ,x2 ,x3 ), f3(x1 ,x2 )}.
Тогда
суперпозициями функций из F будут, например, функции:φ1(x2, x3) = f3( f1(x2), f1(x3));
φ2(x1, x2) = f2 (x1 , f1(x1 ), f3(x1 ,x2 )).
Cовершенная ДНФ - суперпозиция функций из множества
.
Слайд 56 Система функций называется полной, если при помощи операций
суперпозиции и замены переменных из функций этой системы может
быть получена любая функция алгебры логики.
Слайд 57
Мы уже имеем некоторый набор полных систем:
{x+y, xy,
1}.
Как определить условия, при которых система полна?
Слайд 58
Замкнутые классы.
Множество (класс) K функций алгебры логики называется
замкнутым классом, если оно содержит все функции, получающиеся из
K операциями суперпозиции и замены переменных, и не содержит никаких других функций.Пусть K - некоторое подмножество функций из P2(n). Замыканием K называется множество всех булевых функций, представимых с помощью операций суперпозиции и замены переменных функций из множества K. Замыкание множества K обозначается через [K].
В терминах замыкания можно дать другие определения замкнутости и полноты (эквивалентные исходным):
K- замкнутый класс, если K = [K];
K - полная система, если [K] = P2(n).
Слайд 59
Примеры.
{0}, {1} - замкнутые классы.
Множество функции
одной переменной - замкнутый класс.
- замкнутый класс.Класс {1, x+y} не является замкнутым классом.
Слайд 60
Замкнутые классы.
1. Т0 - класс функций, сохраняющих
0.
Обозначим через Т0 класс всех функций алгебры логики f(x1,
x2, ... , xn), сохраняющих константу 0, то есть функций, для которых f(0, ... , 0) = 0.0, x, xy, xy, x+y T0;
1, T0. Из того, что T0 следует, например, что нельзя выразить через дизъюнкцию и конъюнкцию.
Слайд 61 Поскольку таблица для функции f из класса Т0
в первой строке содержит фиксированное значение 0, то для
функций из Т0 можно задавать произвольные значения только на 2n - 1 наборе значений переменных, то есть,
где - множество функций, сохраняющих 0 и зависящих от n переменных.
Покажем, что Т0 - замкнутый класс. Так как xT0 , то для обоснования замкнутости достаточно показать замкнутость относительно операции суперпозиции, поскольку операция замены переменных есть частный случай суперпозиции с функцией x.
Слайд 63
2. T1 - класс функций, сохраняющих 1.
f(1, ...
, 1) = 1
1, x, xy, xy, xy
T1;0,
, x+y T1
Из того, что x + y T1 следует, например, что x + y нельзя выразить
через дизъюнкцию и конъюнкцию.
Слайд 66
Докажем, что xy L .
Предположим противное. Будем
искать выражение для xy в виде линейной функции с
неопределенными коэффициентами:При x = y = 0 имеем =0,
при x = 1, y = 0 имеем = 1,
при x = 0, y = 1 имеем = 1,
но тогда при x = 1, y = 1 имеем 1 1 1 + 1, что доказывает нелинейность функции дизъюнкция xy.
Доказательство замкнутости класса линейных функций очевидно.
Слайд 67 Поскольку линейная функция однозначно определяется заданием значений n+1
коэффициента 0, ... , n , число линейных функций
в классе L(n) функций, зависящих от n переменных равно 2n+1.
Слайд 68
4. S - класс самодвойственных функций.
Функция
, определяемая равенством
называется двойственной к функции
Таблица для двойственной функции (при стандартной упорядоченности наборов значений переменных) получается из таблицы для исходной функции инвертированием (то есть заменой 0 на 1 и 1 на 0) столбца значений функции и его переворачиванием.
Слайд 69
0* = 1,
1* = 0,
x* = x,
(x1
x2)* = x1 x2,
(x1 x2)* = x1
x2.(f*)* = f
функция f является двойственной к f*.
Слайд 70 Теорема. Если функция получена как суперпозиция функций
f, f1, f2, ... , fm, то функция, двойственная
к суперпозиции, есть суперпозиция двойственных функций.Слайд 72 Обозначим через S класс всех самодвойственных функций из
P2:
S = {f | f* = f }
x,
S;
0, 1, xy, xy S .
Для самодвойственной функции имеет место тождество
Слайд 73 На наборах
и
, которые мы будем называть противоположными, самодвойственная функция принимает противоположные значения. Отсюда следует, что самодвойственная функция полностью определяется своими значениями на первой половине строк стандартной таблицы. Поэтому число самодвойственных функций в классе S(n) функций, зависящих от n переменных, равно:Слайд 74 Докажем теперь, что класс S замкнут. Так как
xS , то для обоснования замкнутости достаточно показать замкнутость
относительно операции суперпозиции, поскольку операция замены переменных есть частный случай суперпозиции с функцией x.
Слайд 76
5. М - класс монотонных функций.
Набор
предшествует набору,
если i i для всех i = 1, ... , n.
Наборы α и β называются сравнимыми, если либо α≤β либо β≤α.В случае, когда ни одно из этих оотношений не выполняется, то наборы называются несравнимыми.