- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Натуральные логарифмы
Содержание
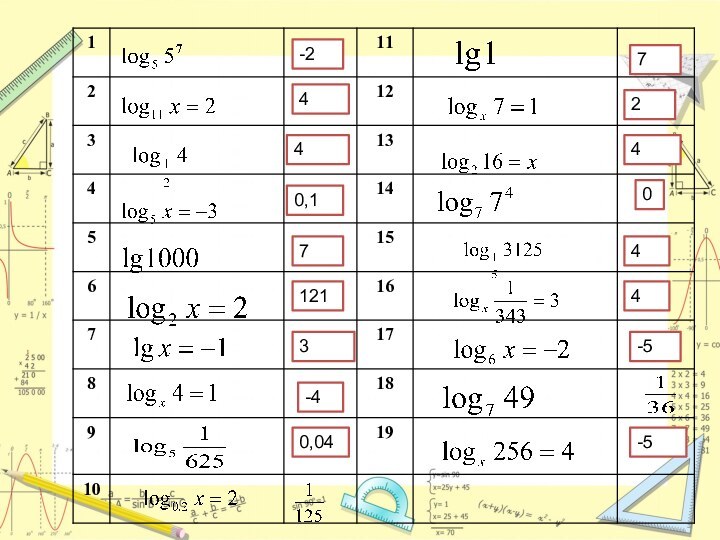
- 2. «Логарифмический дартс»
- 3. 71210,0440,13-44-20-574244-5
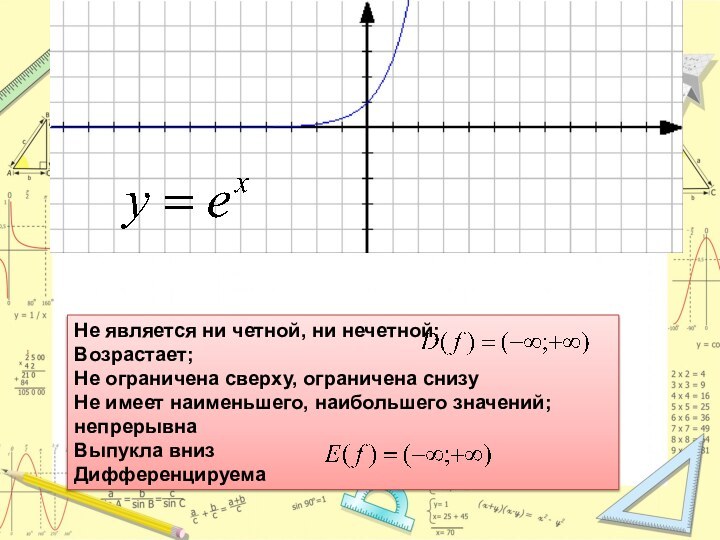
- 5. Не является ни четной, ни нечетной;Возрастает;Не ограничена сверху, ограничена снизуНе имеет наименьшего, наибольшего значений; непрерывнаВыпукла внизДифференцируема
- 7. -ctg x tg x cos x -sin x sin x cos xy= f(kx+b) y=f(x)+g(x)Y=F(x)+G(x)y=kf(x)Y=kF(x)
- 8. =F(b) – F(a).
- 10. Логарифм по основанию е называется натуральным логарифмомДесятичные
- 12. Функция вида y=lnx, свойства и графикНи четна,
- 14. 1633, 1634, 1635, 1636(а,б)Дома: в,г
- 15. №1633
- 16. №1634
- 17. №1635
- 18. №1636
- 19. Составить уравнение касательной к графику функции y=lnx в точке x=e№1623,1637,1641 (а,б)в,г - дома
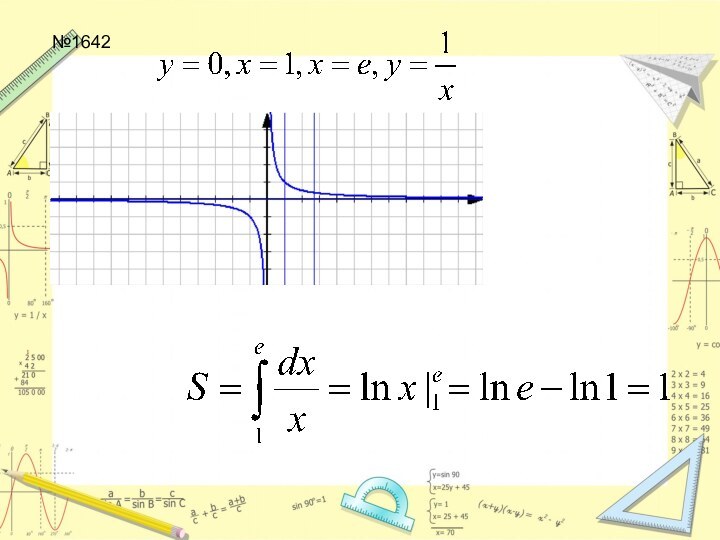
- 20. №1642, 1643
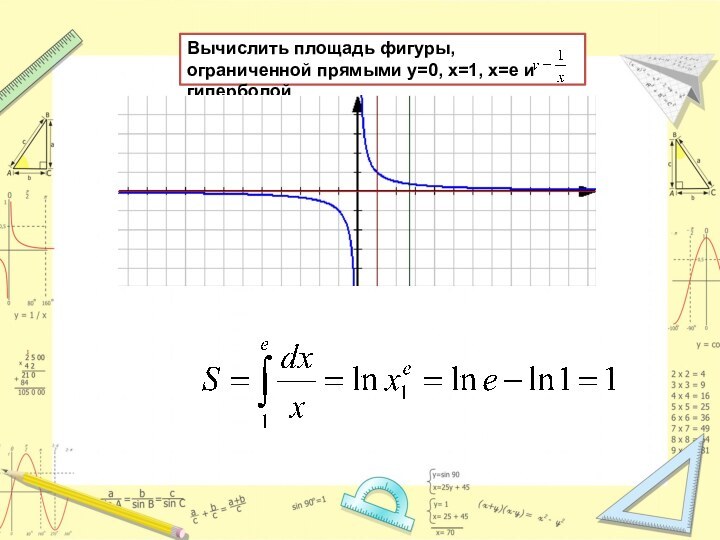
- 21. Вычислить площадь фигуры, ограниченной прямыми y=0, x=1, x=e и гиперболой
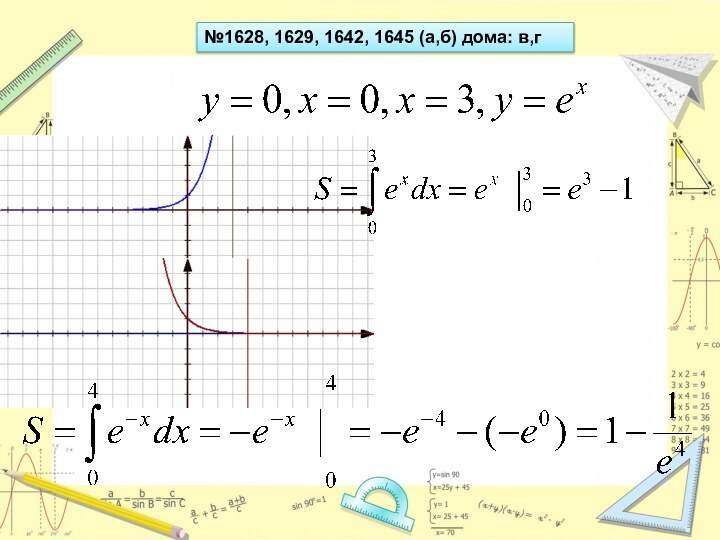
- 22. №1628, 1629, 1642, 1645 (а,б) дома: в,г
- 23. №1629 (а)
- 24. №1629(б)
- 25. №1642
- 26. №1642(б)
- 27. №1645 (а)
- 28. №1645(б)
- 29. Скачать презентацию
- 30. Похожие презентации
«Логарифмический дартс»



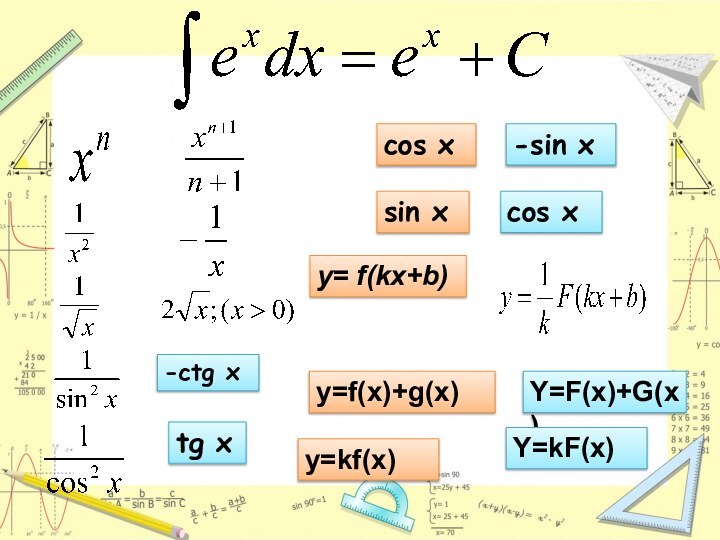



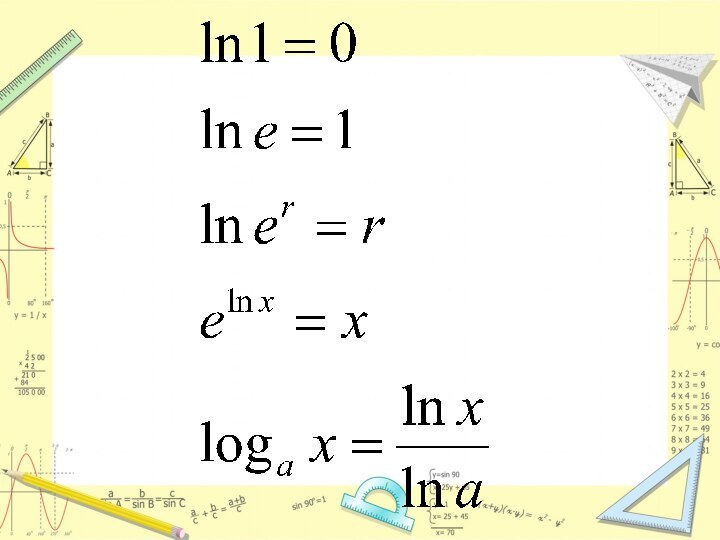















Слайд 10
Логарифм по основанию е называется натуральным логарифмом
Десятичные логарифмы
для наших потребностей являются весьма удобными. Однако при изучении
высшей математики более удобными оказываются логарифмы по основанию е = 2,718281828... (см. § 134, ч. 1). Употребление этих логарифмов позволяет значительно упростить большое количество математических формул. Логарифмы по основанию е получаются при решении многих физических задач и естественным образом входят в математическое описание некоторых химических, биологических и других процессов. Этим и объясняется их название «натуральные логарифмы».Натуральный логарифм числа а обозначается ln а. Сейчас имеются достаточно полные таблицы натуральных логарифмов.
Слайд 12
Функция вида y=lnx, свойства и график
Ни четна, ни
нечетна
Не ограничена ни сверху, ни снизу
Не имеет наибольшего, наименьшего
значенийНепрерывна
Выпукла вверх
дифференцируема