Слайд 3
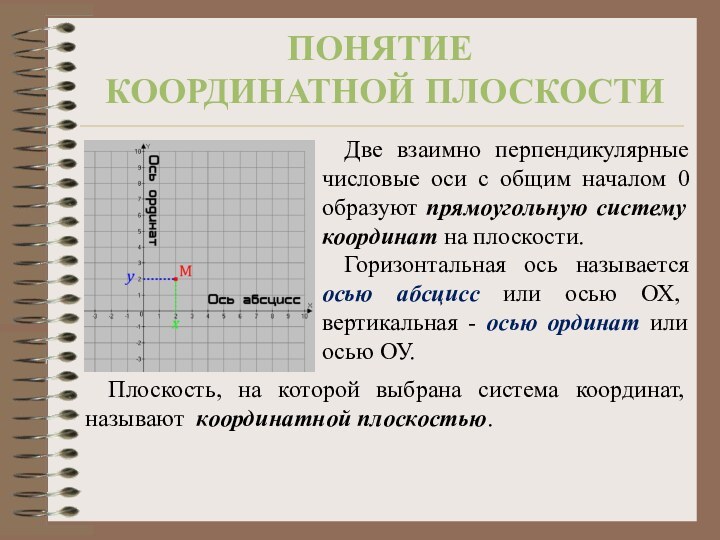
Две взаимно перпендикулярные числовые оси с общим началом
0 образуют прямоугольную систему координат на плоскости.
Горизонтальная ось называется
осью абсцисс или осью ОХ, вертикальная - осью ординат или осью ОУ.
Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Понятие
координатной плоскости
Слайд 4
Координатная плоскость делится осями на четыре части, которые
называются координатными четвер-тями.
Координатные четверти нумеруются против часовой стрелки.
координатные четверти
Слайд 5
Пусть М - произвольная точка координатной плоскости.
Координата проекции
точки М на ось ОХ называется абсциссой точки М,
координата проекции точки М на ось ОУ называется ординатой точки М.
Абсциссу и ординату точки М называют координатами точки М. При этом записывают М (х, у) (на первом месте всегда пишут абсциссу).
! Каждой паре чисел х и у соответствует единственная точка М координатной плоскости с координатами (х, у). Значит, координаты х и у определяют положение точки на плоскости.
Точка на координатной
плоскости
Слайд 6
Функция может быть задана с помощью ее графика.
На
координатной плоскости 0ХУ для каждого значения х из множества
D (области определения функции) строится точка М (х, у), абсцисса которой равна х, а ордината - соответствующему значению функции у(х). Построенные точки образуют некоторую линию, которую называют графиком данной функции.
Графический способ
Задания функции
Слайд 7
Чтобы по заданному графику найти значение функции у(х)
при каком-то определенном значении х, нужно провести через точку
х оси абсцисс перпендикуляр к этой оси и найти точку пересечения перпендикуляра с графиком данной функции.
Чтобы по заданному графику найти при каком значении аргумента х функция принимает определенное значение у, нужно провести через точку у оси ординат перпендикуляр к этой оси и найти все точки пересечения его с графиком функции.
Абсциссы точек пересечения его с графиком функции дают соответствующие значения аргумента.
Работа с графиком
Слайд 8
Свойства функции
Числовое множество называется симметричным относительно начала координат,
если этому множеству вместе с числом х принадлежит и
противоположное ему число -х.
Функция у = f(x) называется
если выполняются два условия:
1)
Слайд 9
Свойства функции
2) Для любого x из области определения
функции выполняется равенство:
III. Возрастание и убывание функции
Функция у
= f(х) называется возрастающей (убывающей) на некотором промежутке, если для любых двух значений х из этого промежутка большему значению аргумента соответствует большее (меньшее) значение функции, т.е. из условия х1< х2 следует, что f(х1)f(х2))
Слайд 10
Свойства функции
IV. Промежутки знакопостоянства функции. Промежутки в которых
функция сохраняет свой знак (то есть остаётся положительной или
отрицательной) называют промежутками знакопостоянства функции
V. Нули функции.
Значения аргумента х в которых f(х)=0 называются нулями функции.
Слайд 11
Линейная функция
Линейной называется функция вида у = kх
+ b,
где k и b действительные числа.
k
0, b 0
Y = 2x-1
Графиком линейной функции является прямая линия. Для того, чтобы построить прямую доста-точно построить две точ-ки. Рассмотрим различные случаи линейной функции
Слайд 12
Линейная функция
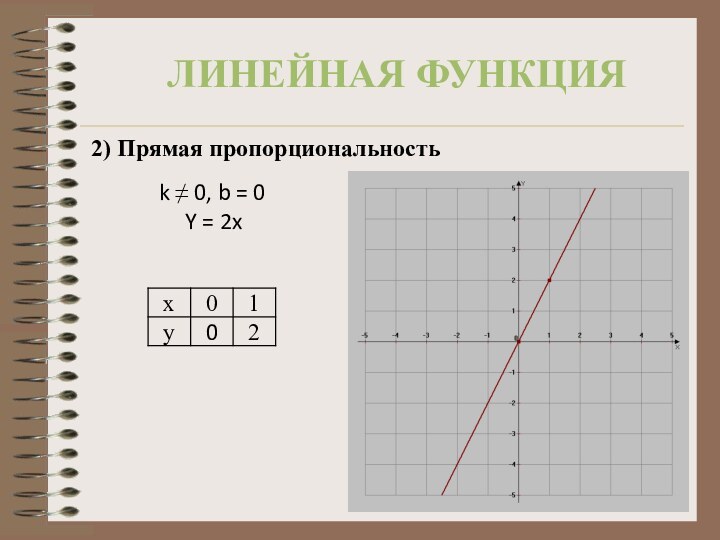
2) Прямая пропорциональность
k 0, b
= 0
Y = 2x
Слайд 13
Линейная функция
3)
k = 0, b 0
Y
Слайд 17
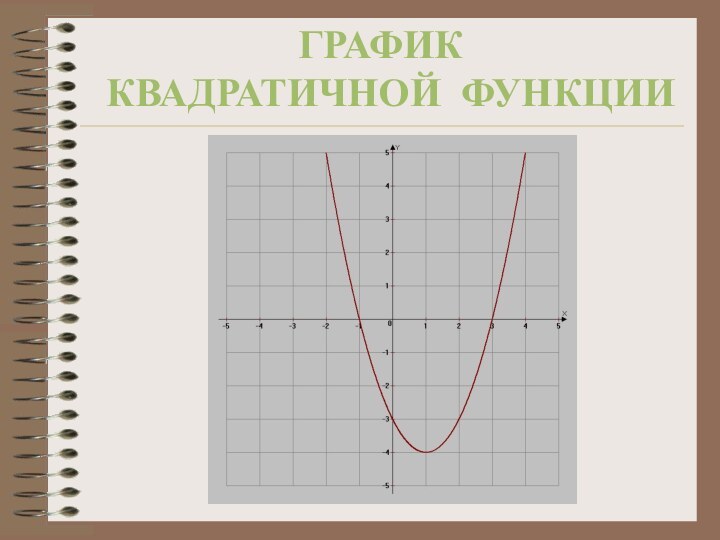
Квадратичная функция
Построим график функции
a = 1, ветви параболы
направлены вверх
Найдем координаты вершины
Ось симметрии параболы x = 1
Найдем
координаты точек пересечения с осью ОХ. Для этого решим уравнение
Координаты точки пересечения с осью OY
x=0; y = -3;
Слайд 19
Кубическая функция
График функции — кубическая парабола
Составим таблицу значения
функции в 5-ти точках:
Свойства функции y=x3
Область определения: множество всех
действительных чисел
Множество значений: множество всех действительных чисел
Функция нечетная
Нули функции: y=0 при x=0
Функция возрастает на всей области определения
Слайд 21
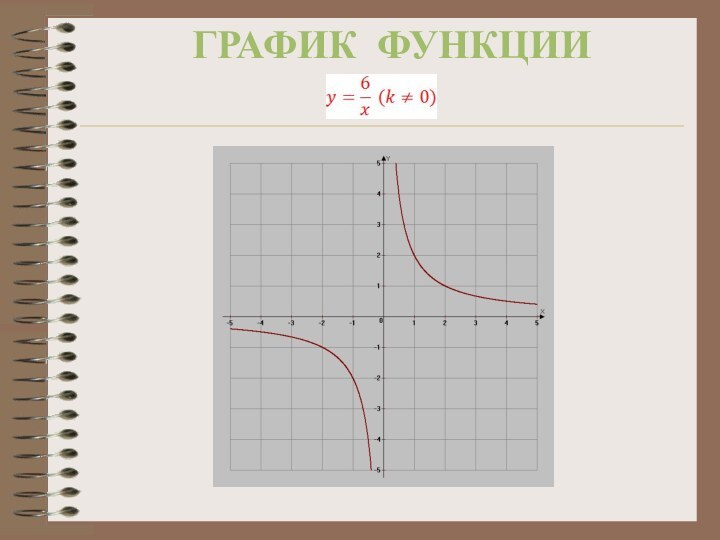
функция
График функции — гипербола.
При построении графика функции удобно
брать те значения аргумента, которые являются делителями числа k.
Построим график для функции
Если k<0, то график функции расположен во II и IV координатных областях
Свойства функции:
Область определения: промежутки (-; 0) и (0; )
Множество значений: x0
Функция нечетная.
Слайд 22
Нулей нет.
Промежутки монотонности:
Если k>0, то функция убывает на
промежутках
(-; 0) и (0; )
Если k
возрастает на промежутках
(-; 0) и (0; )
Промежутки знакопостоянства
Если k>0, то
Если k<0, то
Свойства функции
Слайд 24
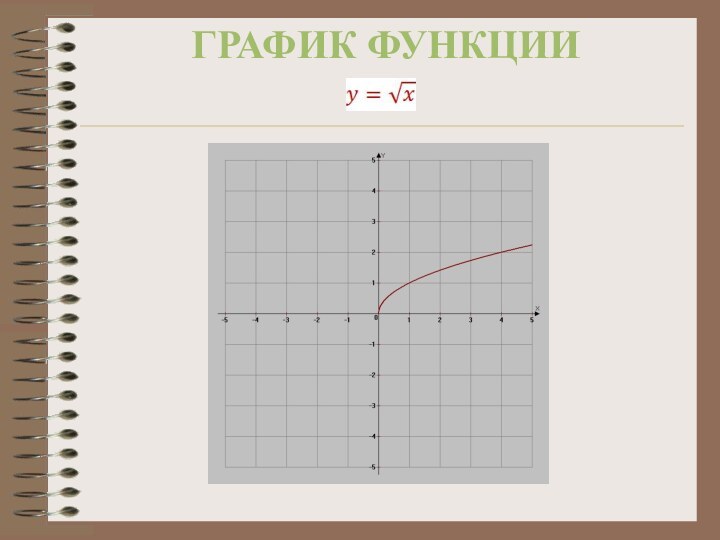
функция
При построении графика удобно брать те значения аргумента,
из которых легко извлекаются квадратный корень.
Свойства функции:
Область определения: x0
Множество
значений: y0
Функция не является четной и не является нечетной
Нули: y=0, при x=0
Промежутки монотонности: функция возрастает на всей области определения
Промежутки знакопостоянства: y>0, при x>0
Слайд 27
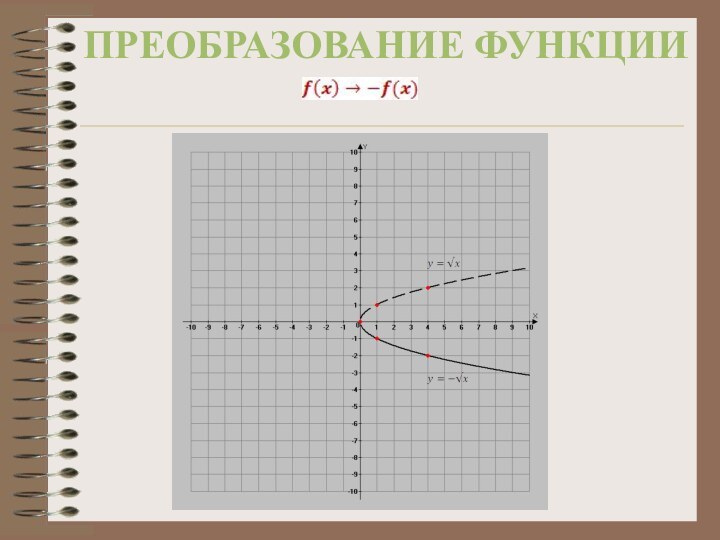
преобразование функции
Чтобы построить график функции
, нужно:
Построить график
Отобразить его
симметрично относительно оси ОХ
ВНИМАНИЕ! Точки пересечения графика с осью ОХ остаются на месте.
Слайд 28
преобразование функции
Пример.
Построить график функции
Решение. Построим график
функции
по контрольным точкам, а затем отобразим его симметрично относительно оси ОХ.
Слайд 30
преобразование функции
Чтобы построить график функции
, нужно:
Построить график функции
;
Отобразить его симметрично относительно оси ОУ.
Слайд 31
преобразование функции
Пример.
Построить график функции
Решение.
Построим график функции
по контрольным точкам, а затем отобразим его симметрично относительно оси ОУ.
Слайд 33
преобразование функции
Чтобы построить график функции
, нужно:
Построить график
функции ;
Переместить его вдоль оси ОХ вправо, если а<0 и влево, если а>0 на |а| единиц
Слайд 34
преобразование функции
Пример.
Построить графики функции
и
Решение.
Построим график
функции у=х2 по контрольным точкам.
Для построения графика у=(х-2)2, перенесем его на 2 единицы вправо.
Для построения графика у=(х+3)2, перенесем его на 3 единицы влево
Слайд 36
преобразование функции
Чтобы построить график функции
, нужно:
Построить график
функции ;
Переместить его вдоль оси ОУ вверх, если b>0 и вниз, если b<0 на |b| единиц.
Слайд 37
преобразование функции
Пример.
Построить график функции
и
Решение.
Построим график
функции
Для построения функции перенесем его на 2 единицы вверх вдоль оси ОУ.
Для построения функции перенесем его на 2 единицы вниз вдоль оси ОУ.
Слайд 39
преобразование функции
Чтобы построить график функции
, нужно:
Построить график функции
;
Если α>1, сжать его вдоль оси ОХ в α раз;
Если 0<α<1, растянуть его вдоль оси ОХ в раз.
ВНИМАНИЕ! Точки пересечения графика с осью ОУ остаются на месте.
Слайд 40
преобразование функции
Пример.
Построить графики функций
,
Решение.
Построим график функции
по контрольным точкам.
При построении графика функции уменьшим абсциссы контрольных точек в 3 раза, а ординаты оставим без изменения.
При построении графика функции увеличим
абсциссы контрольных точек в 3 раза, а ординаты оставим без изменения.
Слайд 42
преобразование функции
Чтобы построить график функции
, нужно:
Построить график функции
;
Если к>1, растянуть график его вдоль оси ОУ в к раз;
Если 0<к<1, сжать его вдоль оси ОУ в раз.
ВНИМАНИЕ! Точки пересечения графика с осью ОХ остаются без изменения.
Слайд 43
преобразование функции
Пример.
Построить графики функций
и
Решение.
Построим график функции
по контрольным точкам.
При построении графика функции ординаты контрольных точек увеличим в два раза, а абсциссы оставим без изменения.
При построении графика функции ординаты контрольных точек уменьшим в два раза, а абсциссы оставим без изменения.
Слайд 45
преобразование функции
Чтобы построить график функции
, нужно:
Построить график функции
;
Части графика , лежащие ниже оси ОХ отобразить симметрично относительно оси ОХ.
Части графика , лежащие выше или на оси ОХ оставить без изменения.
ВНИМАНИЕ! График функции целиком расположен в верхней полуплоскости.
Слайд 46
преобразование функции
Пример.
Построить график функции
;
Решение.
1. Построим
график функции . Для этого построим график функции по контрольным точкам, а затем сместим его на 2 единицы вниз вдоль оси ОУ.
2. Часть графика функции , лежащего ниже оси ОХ отобразим симметрично относительно этой оси.
Слайд 48
преобразование функции
Чтобы построить график функции
, нужно:
Построить график функции
;
Часть графика, лежащую левее оси ОУ удалить.
Часть графика лежащего правее оси ОУ достроить симметрично относительно этой оси.
ВНИМАНИЕ! Функция четная (ее график симметричен относительно оси ОУ). Поэтому при построении графика функции можно строить лишь ту часть графика , которая лежит правее оси ОУ, т.е. строить график функции на области определения х≥0.
Слайд 49
преобразование функции
Пример.
Построить график функции
Решение.
Построим график
функции
. Для этого график функции у=х2 сместим на 1 единицы вправо вдоль оси ОХ и на 1 единицы вниз вдоль оси ОУ.
Часть графика, расположенную левее оси ОУ удалим.
Часть графика, расположенную правее оси ОУ достроим симметрично относительно этой оси.
Замечание. Все эти преобразования выполняются на одном чертеже.
Слайд 51
Построение графиков сложных функций с помощью последовательных преобразований
графиков элементарных функций
Чтобы построить график сложной функции, нужно:
Выделить
элементарную функцию, лежащую в основе графика.
Выписать последовательно преобразования, касающиеся аргумента функции и выполнить их в обратном порядке.
Выписать последовательно преобразования, касающиеся функции в целом и выполнить их в том порядке, в котором они записаны.