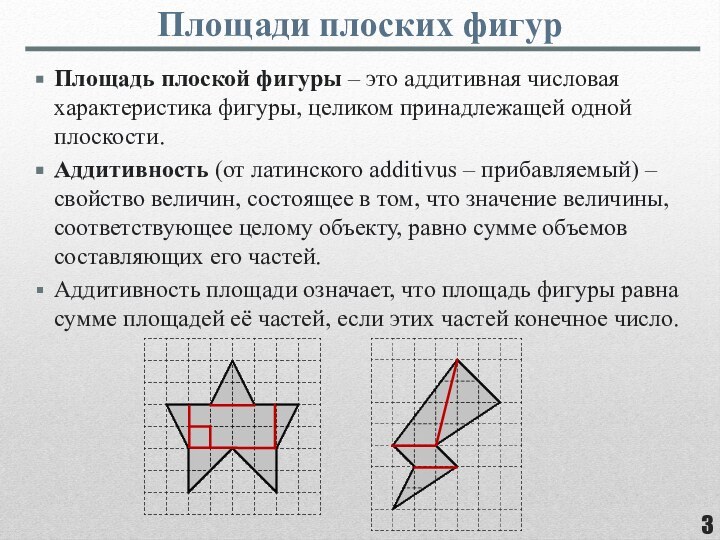
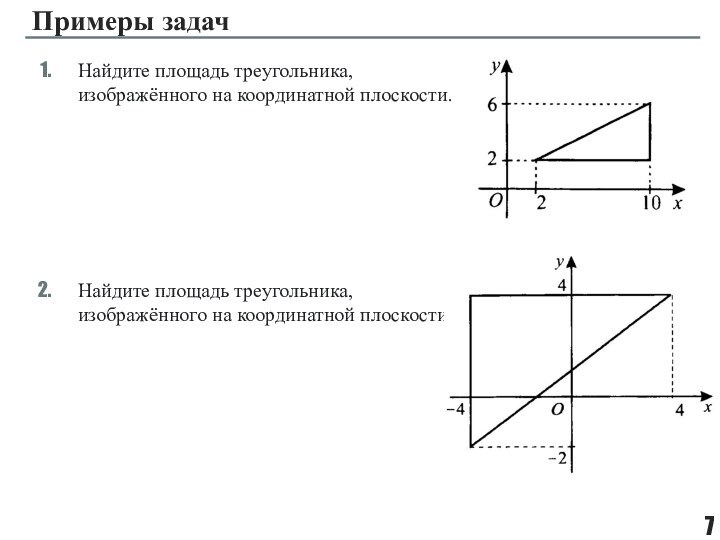
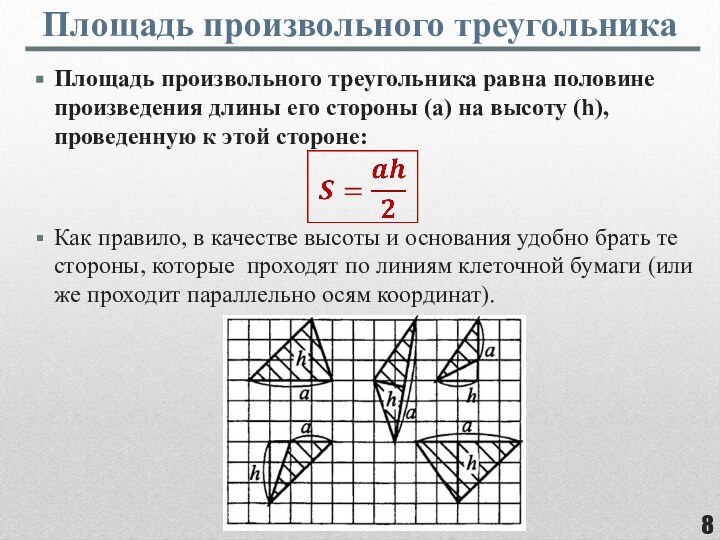
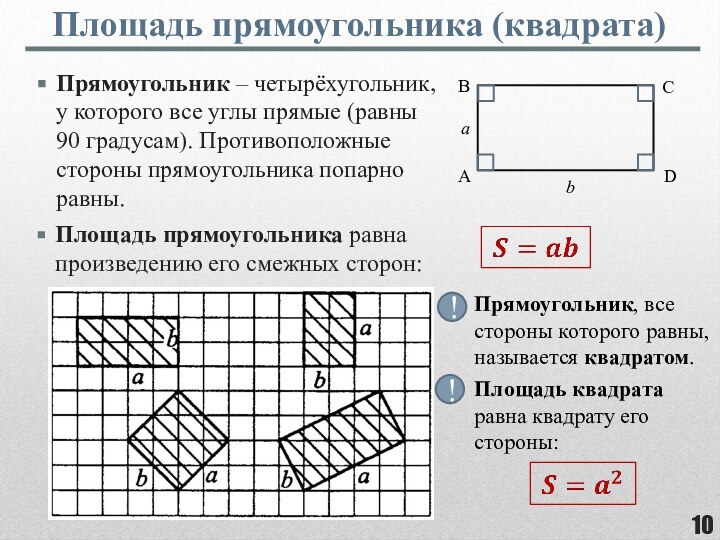
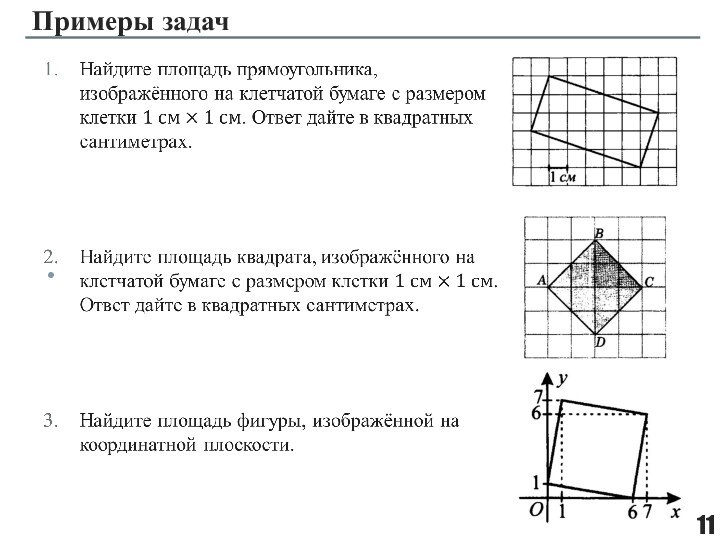
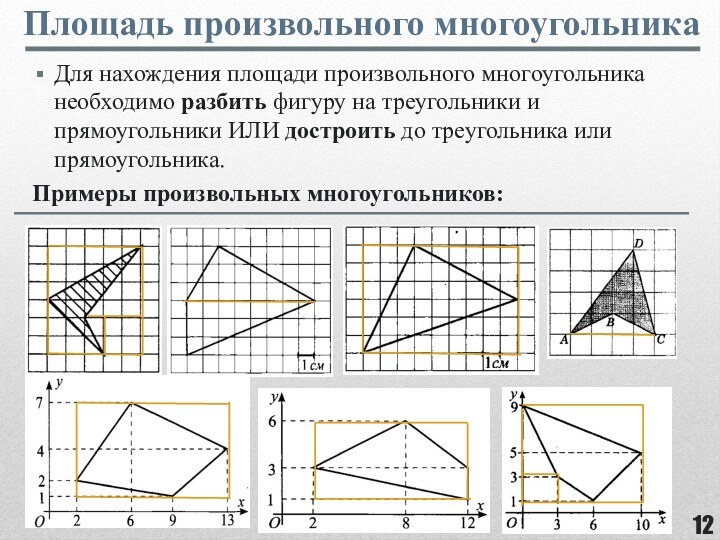
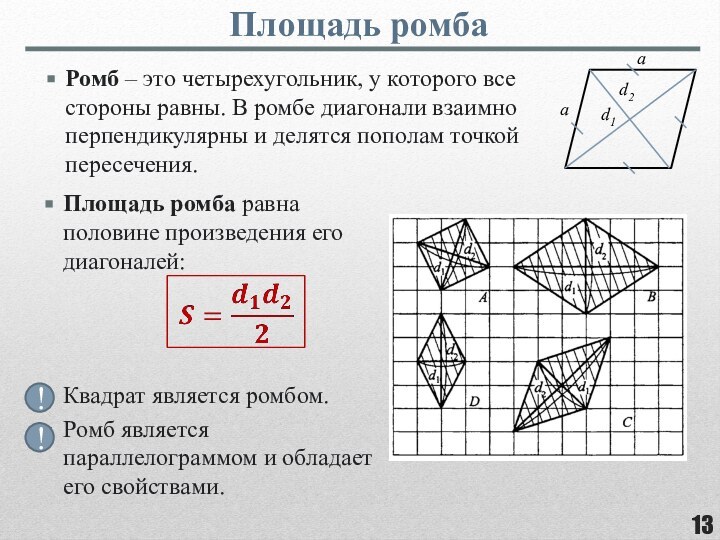
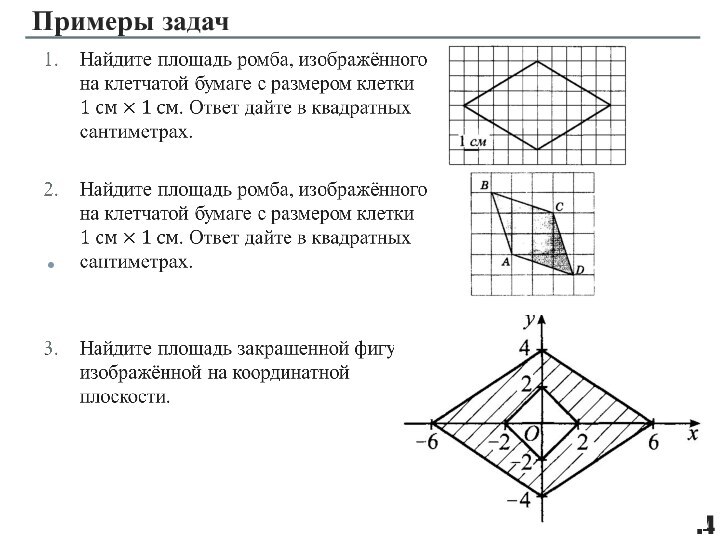
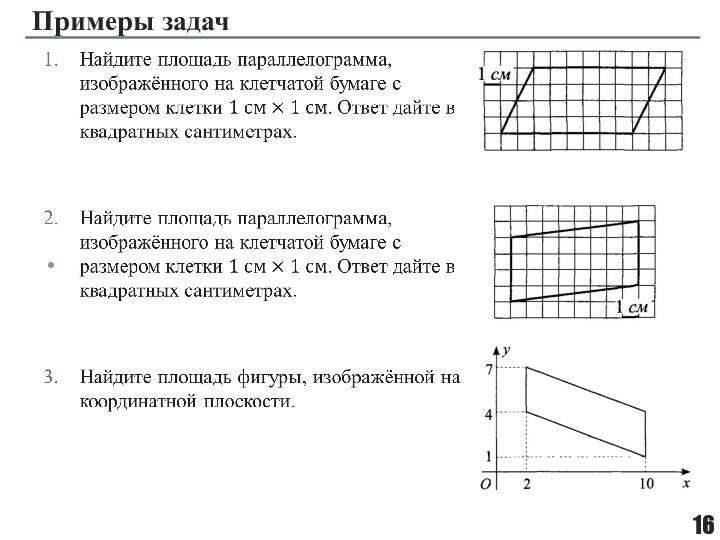
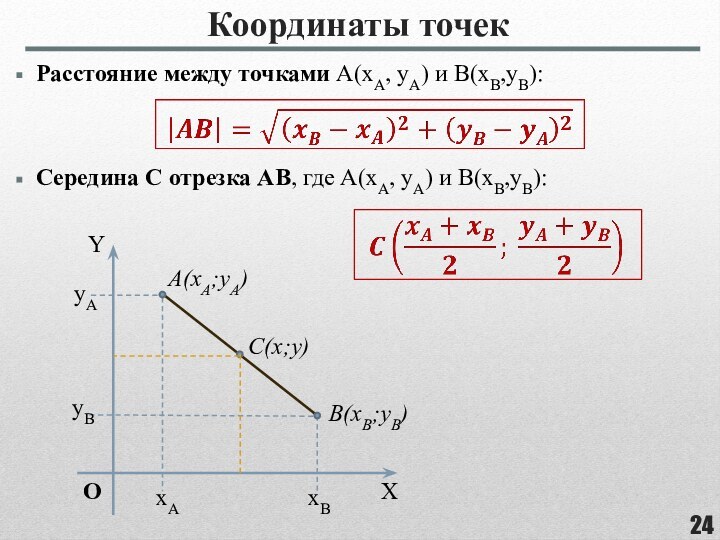
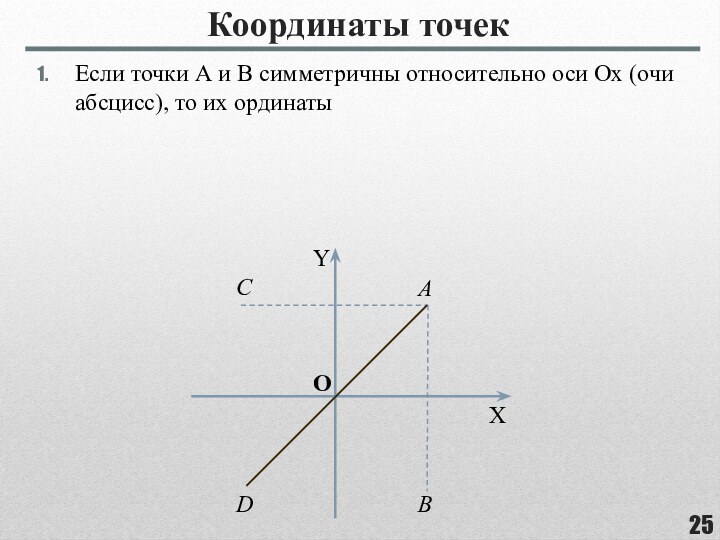
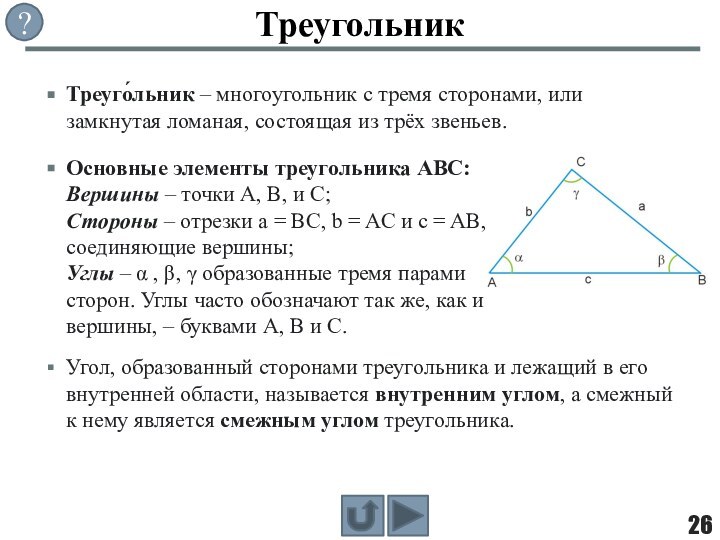
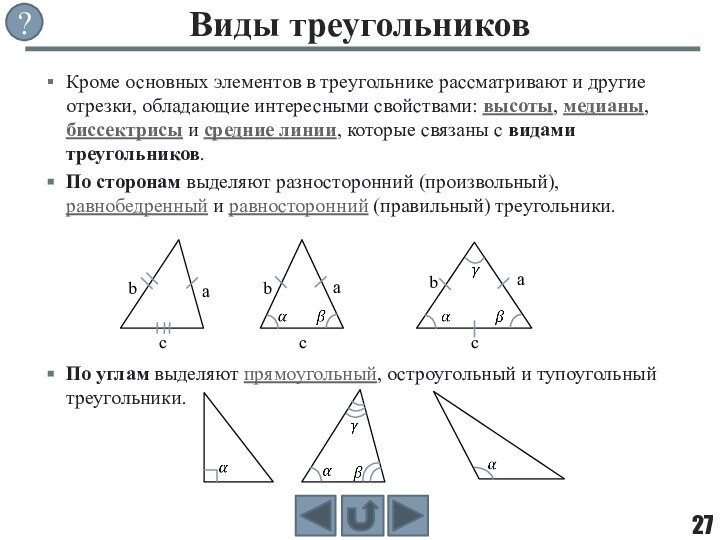
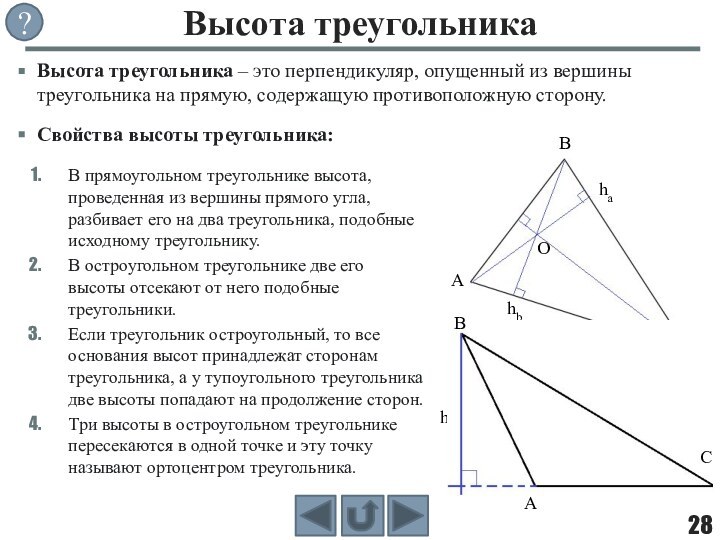
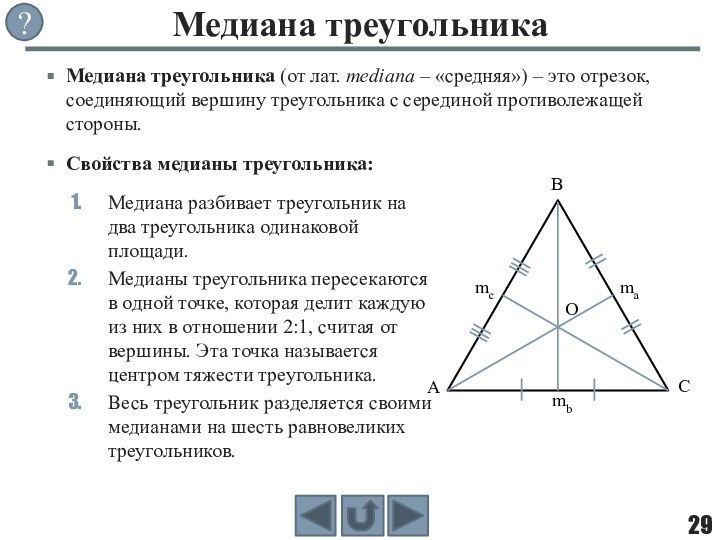
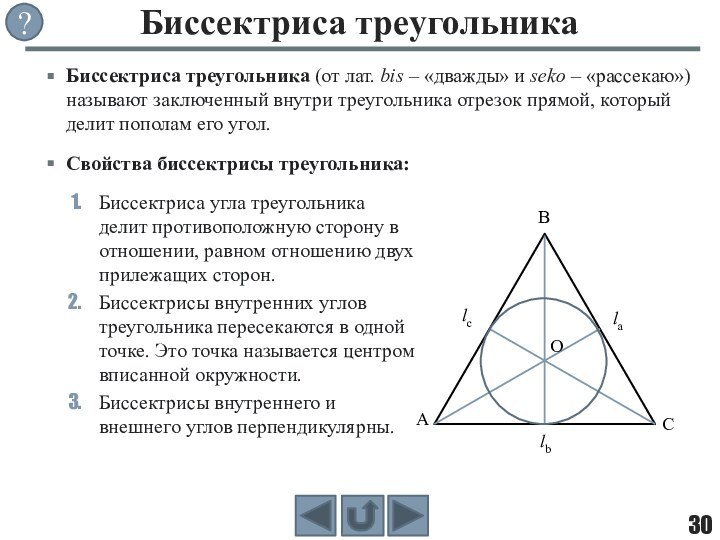
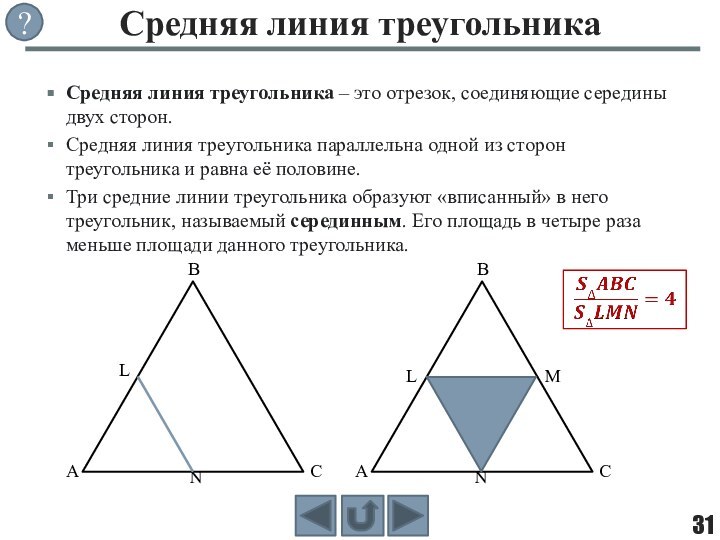
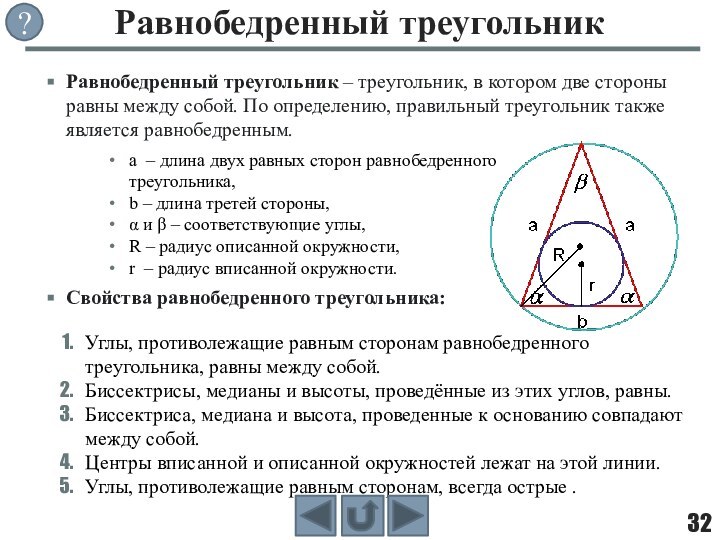
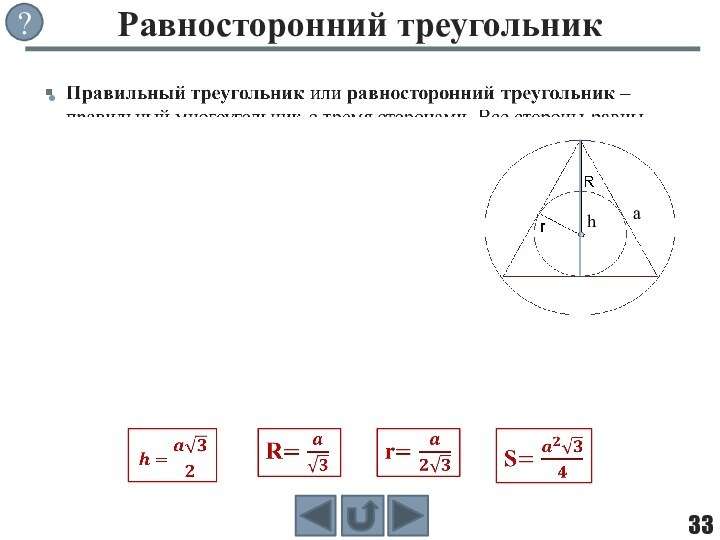
фигуры, целиком принадлежащей одной плоскости.
Аддитивность (от латинского additivus –
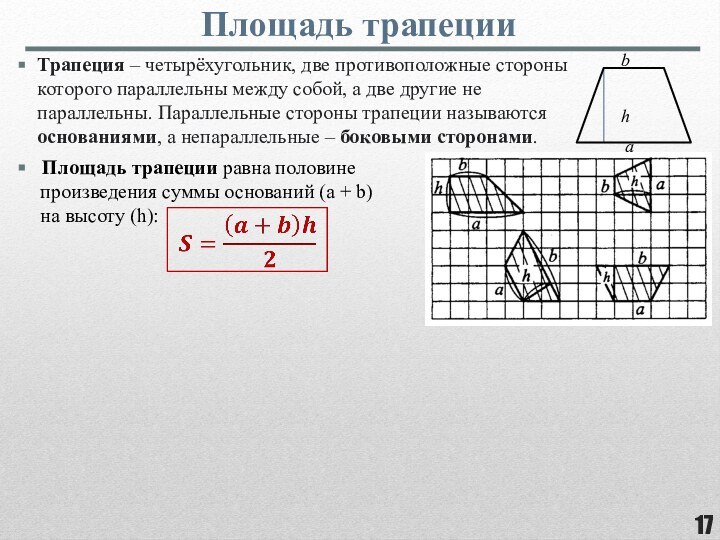
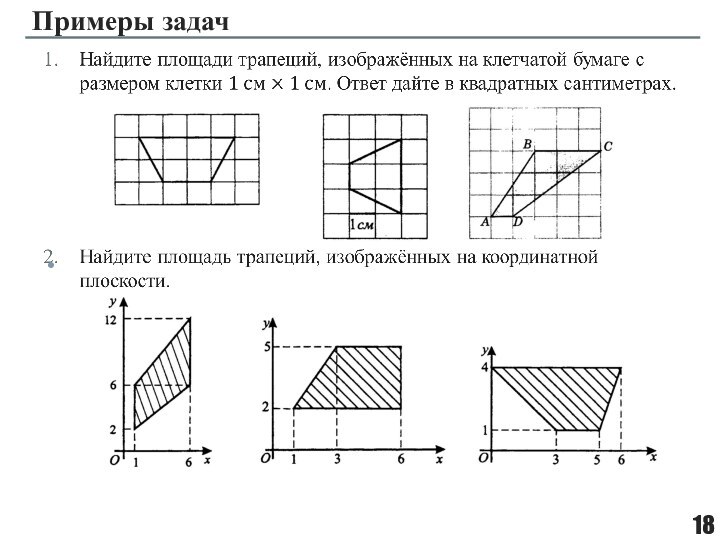
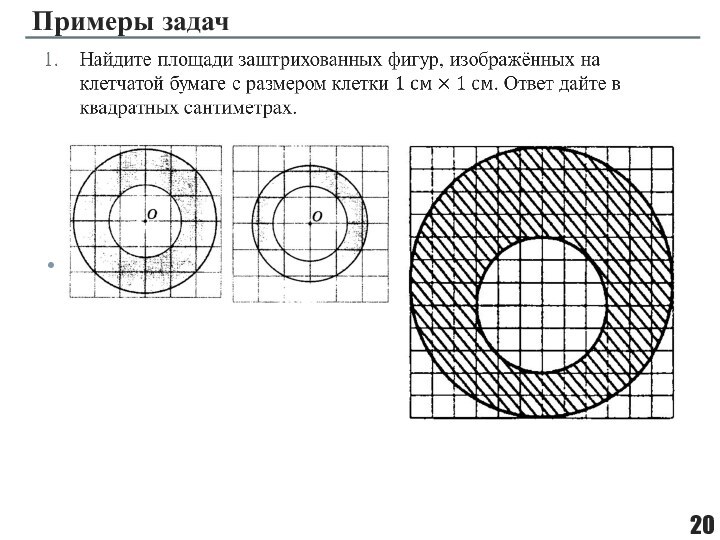
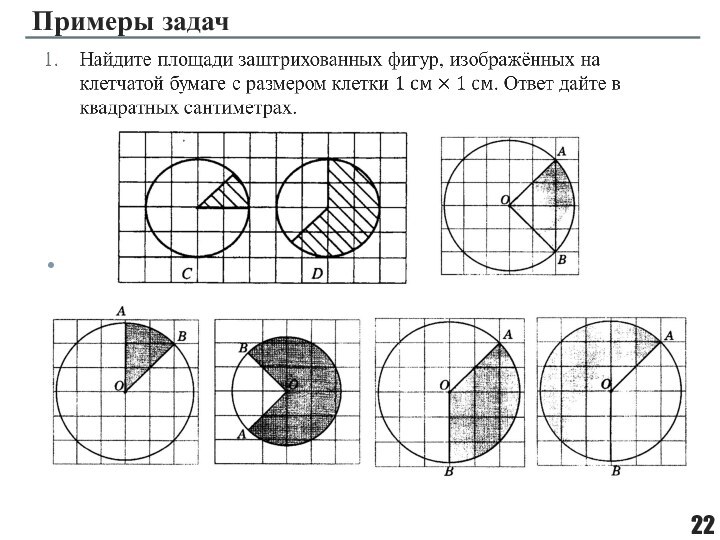
прибавляемый) – свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме объемов составляющих его частей.Аддитивность площади означает, что площадь фигуры равна сумме площадей её частей, если этих частей конечное число.
Площади плоских фигур