Слайд 2
План
Теорема о корне монотонной функции
Возрастание синуса на отрезке
[−π/2; π/2]
Определение арксинуса числа
График синуса на отрезке [−π/2; π/2]
Примеры
Определение
арккосинуса числа
Определение арктангенса числа
Определение арккотангенса числа
Слайд 3
Теорема о корне
монотонной функции
Пусть функция f(x) возрастает (убывает) на
промежутке
, а число а – любое из значений функции f из множества значений. Тогда уравнение f(x) = a имеет единственный корень в промежутке .
Слайд 4
Доказательство
Доказательство для возрастающей функции.
По условию число а
– какое-либо значение функции f, т.е. в промежутке
q> существует такое число b, что f(b) = a. Докажем единственность.
Слайд 5
От противного. Допустим, на промежутке есть еще одно
число с ≠ b, такое что
f(c) =
a.
Но а = f(b), т.е. f(c) = f(b). Так как с ≠ b, то для определенности пусть c > b. Но функция f возрастает на
, поэтому f(c) > f(b). Это противоречит равенству f(c) = f(b).
Слайд 6
Следовательно, число b одно, т.е. на промежутке
q> функция f имеет единственный корень.
Теорема доказана.
Слайд 7
Возрастание синуса
на отрезке [−π/2; π/2]
Функция синус на
отрезке [−π/2; π/2] возрастает. Докажем это.
Пусть х1, х2
(−π/2; π/2) и х1 < x2. Надо показать, что sinx1 < sinx2.
Или разность sinx2 – sinx1 > 0.
sinx2 – sinx1=
Слайд 8
Имеем неравенства
,
Сложим − π < х1 + х2 < π ,
Сл-но,
Рассмотрим два неравенства:
Слайд 9
Сложим < х2 – х1 < .
Учтем, что х1 < x2 , т.е. х2 –
х1 > 0.
Получим
Следовательно, синус этого числа > 0.
Доказали, что синус возрастает на отрезке [−π/2; π/2] .
Слайд 10
Определение
арксинуса числа
Функция синус принимает значения из
отрезка [−
1; 1]. Рассмотрим уравнение
sinx = a, где | a
| ≤ 1.
По теореме о корне уравнение sinx = a
имеет один корень b из отрезка [−π/2; π/2] такой, что sinb = a.
Это число b называется арксинусом
числа а. Обозначают arcsin a.
Слайд 11
Арксинусом числа а из отрезка [− 1; 1]
называется такое число из отрезка [−π/2; π/2], синус которого
равен а.
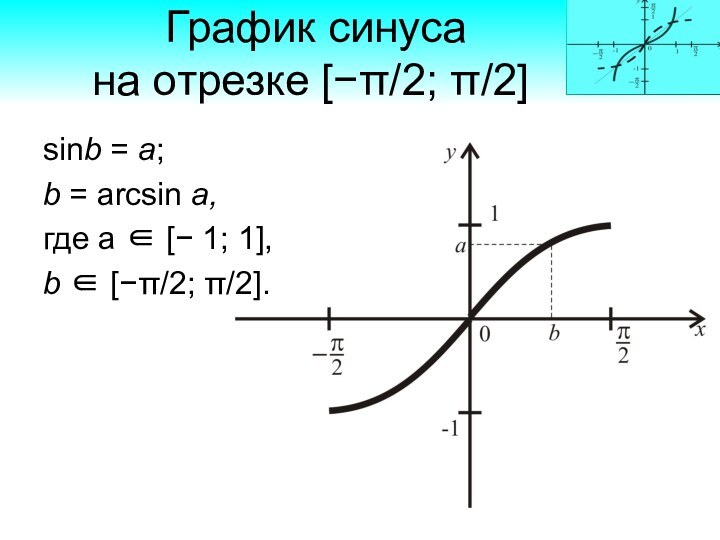
синуса
на отрезке [−π/2; π/2]
sinb =
a;
b = arcsin a,
где а [− 1; 1],
b [−π/2; π/2].
Слайд 13
Чему равен arcsin
следующих чисел?
arcsin0 =
Ответ: arcsin0
= 0.
2. arcsin1 =
Ответ: arcsin1 = π/2.
3.
arcsin(1/2) =
Ответ: arcsin(1/2) = π/6.
4. arcsin2
ТАК НЕЛЬЗЯ ПИСАТЬ!
Слайд 14
5. arcsin(−1) =
Ответ: arcsin(−1) = −
π/2.
6. arcsin(− 1/2) =
Ответ: arcsin(− 1/2) =
− π/6.
Слайд 15
Определение
арккосинуса числа
Функция косинус убывает на отрезке [ 0;
π].
(доказательство аналогично).
Рассмотрим уравнение
cosx = a, где | a |
≤ 1.
По теореме о корне это уравнение имеет один корень b из отрезка [ 0; π] такой, что
cosb = a.
Слайд 16
Это число называется арккосинусом
числа а. Обозначают
arccos a.
Арккосинусом числа а из отрезка [− 1;
1]
называется такое число из отрезка [ 0; π],
косинус которого равен а.
Слайд 17
График косинуса
на отрезке [ 0; π]
cosb = a;
b
= arccos a,
где а [− 1; 1],
b
[ 0; π].
Слайд 18
Чему равен arccos
следующих чисел?
arccos0 =
Ответ: arccos0
= π/2.
2. arccos1 =
Ответ: arccos1 = 0.
3.
arccos(1/2) =
Ответ: arccos(1/2) = π/3.
4. arccos(3/2)
ТАК НЕЛЬЗЯ ПИСАТЬ!
Слайд 20
Определение
арктангенса числа
Функция тангенс возрастает на интервале (−π/2; π/2).
Ее множество значений – это R.
Рассмотрим уравнение tgx =
a, где а – любое число.
На промежутке возрастания, т.е. на
интервале (−π/2; π/2) это уравнение имеет один корень b такой, что tgb = a.
Слайд 21
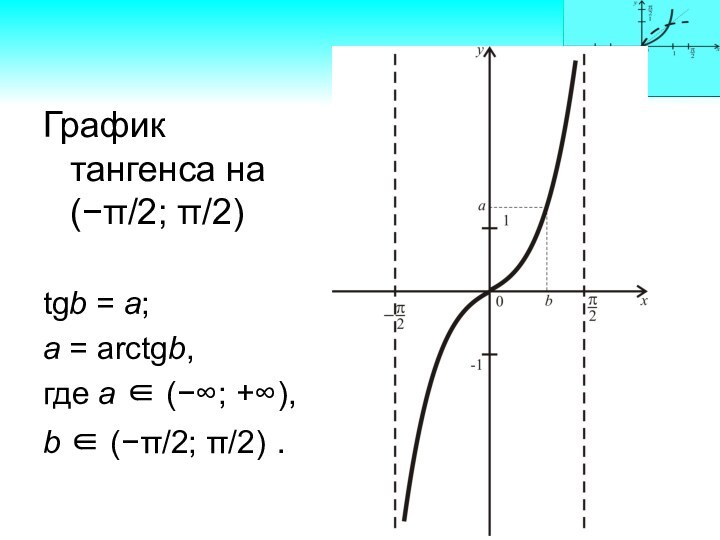
График тангенса на (−π/2; π/2)
tgb = a;
a =
arctgb,
где а (−∞; +∞),
b (−π/2; π/2) .
Слайд 22
Это число называется арктангенсом числа а и обозначают
arctg a.
Арктангенсом числа а, где а
– любое число, называется такое число из интервала (−π/2; π/2), тангенс которого равен а.
Слайд 23
Определение
арккотангенса числа
Функция котангенс убывает на интервале (0; π).
Ее множество значений – это R.
Рассмотрим уравнение ctgx =
a,
где а – любое число.
На промежутке убывания, т.е. на
интервале ( 0; π) это уравнение имеет один корень b такой, что ctgb = a.
Слайд 24
Это число называется арккотангенсом числа а и
обозначают arcctg a.
Арккотангенсом числа а, где
а – любое число, называется такое число из интервала ( 0; π), котангенс которого равен а.
Слайд 25
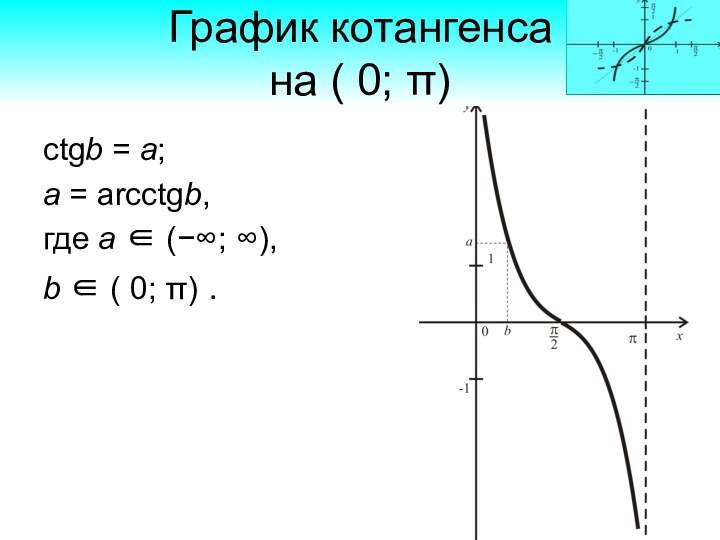
График котангенса
на ( 0; π)
ctgb = a;
a
= arcctgb,
где а (−∞; ∞),
b ( 0;
π) .

![Определение чисел arcsina, arccosa,arctga, arcctga ПланТеорема о корне монотонной функцииВозрастание синуса на отрезке [−π/2; π/2]Определение арксинуса числаГрафик](/img/tmb/14/1327214/cf6f2315c9caf3e43df5d74ae082aa18-720x.jpg)




![Определение чисел arcsina, arccosa,arctga, arcctga Возрастание синуса на отрезке [−π/2; π/2] Функция синус на отрезке [−π/2; π/2]](/img/tmb/14/1327214/02eb256c19b76e74d6f6056d830dea58-720x.jpg)


![Определение чисел arcsina, arccosa,arctga, arcctga Определение арксинуса числаФункция синус принимает значения изотрезка [− 1; 1]. Рассмотрим](/img/tmb/14/1327214/98ed52c4dc8d4c1d40a09a9a90b2805f-720x.jpg)
![Определение чисел arcsina, arccosa,arctga, arcctga Арксинусом числа а из отрезка [− 1; 1] называется такое число из](/img/tmb/14/1327214/730144d36b491310e6ac9a5af75b944e-720x.jpg)


![Определение чисел arcsina, arccosa,arctga, arcctga Определение арккосинуса числаФункция косинус убывает на отрезке [ 0; π].(доказательство аналогично).Рассмотрим уравнениеcosx](/img/tmb/14/1327214/70f3e520431f08e73de271c77730e274-720x.jpg)

![Определение чисел arcsina, arccosa,arctga, arcctga График косинуса на отрезке [ 0; π]cosb = a;b = arccos a,где](/img/tmb/14/1327214/b177b2f8ef36670f1a06e9be326d7d13-720x.jpg)