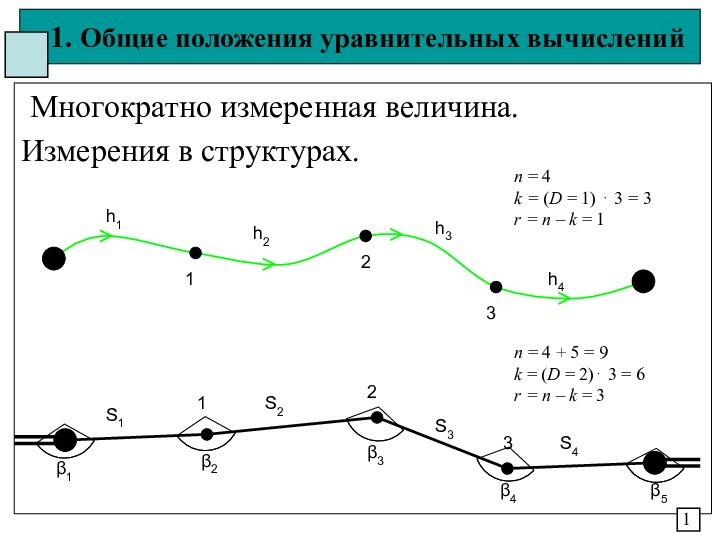
задачи обработки в структурах (геодезических построениях):
Наличие избытка r;
Погрешности измерений
Δ.Наличие избытка – возникновение математических условий r = n – k.
Наличие избытка – неопределенность, оценка качества.
Избыток – погрешности – обработка.
Обработка: количество (уравнивание)
качество (оценка точности)
2









![Общие положения уравнительных вычислений. Многократно измеренная величина. Измерения в структурах 1. Общие положения уравнительных вычисленийФ = [pv2] = minНО - при](/img/tmb/15/1442807/ff33f6fd34d9e59c18b8b2d879d957e3-720x.jpg)