- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Общие принципы проверки статистических гипотез. (Лекция 2)
Содержание
- 2. Общие принципы проверки статистических гипотез: Статистические гипотезыУровень статистической значимостиОсь значимости
- 3. Определение. Генеральная совокупность — это вся подлежащая
- 4. Определение. Выборкой называется любая подгруппа элементов (испытуемых, респондентов), выделенная из генеральной совокупности для проведения эксперимента.
- 5. Определение. Выборочное исследование – это исследование, при
- 6. Выборки называются независимыми (несвязными), если процедура эксперимента
- 7. Выборки называются зависимыми (связными) если процедура
- 8. Требования к выборке:1. Однородность. Выбор
- 9. Смысл статистических методов заключается в
- 10. Числовые значения, характеризующие генеральную совокупность, называются
- 11. В силу действия случайных вероятностных причин
- 12. Предположения о свойствах и параметрах генеральной совокупности
- 13. Статистические гипотезы:Нулевая гипотеза –
- 14. Гипотезы:Направленные гипотезы:H0: X1 не превышает X2 ;H1:
- 15. Определение. Правило, по которому принимается решение принять
- 16. Статистическая проверка гипотез, основан-ная на экспериментальных, выборочных
- 17. Ошибки исследователя:
- 18. Проблема: Как определить, где проходит линия между принятием и отвержением сформулированной исследователем гипотезы?
- 19. Определение. Уровнем значимости называется вероятность ошибочного отклонения
- 20. В прикладных науках, использующих статистику, считается, что
- 21. Правило принятия статистического выводаНа основании полученных экспериментальных
- 22. Величины Чкр1 и Чкр2 находятся для данного
- 23. Сравнение полученного эмпирического значения с критическими (табличными)
- 24. Ось значимости
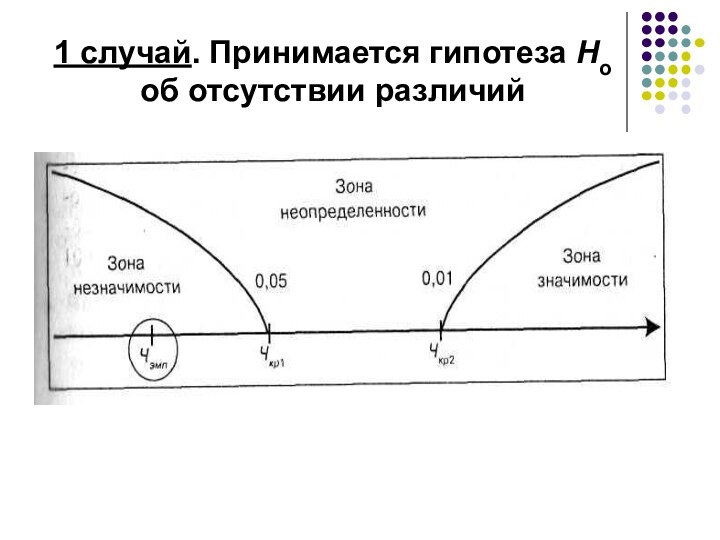
- 25. 1 случай. Принимается гипотеза Но об отсутствии различий
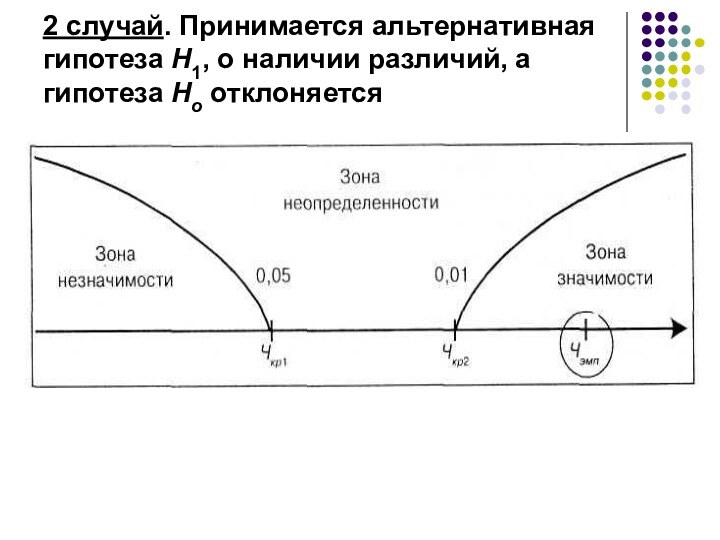
- 26. 2 случай. Принимается альтернативная гипотеза Н1, о наличии различий, а гипотеза Но отклоняется
- 27. 3 случай. Возможность допустить ошибки 1-ого или 2-ого рода
- 28. 3 случай. Возможные варианты статистического выводаВ зависимости
- 29. Замечание. При описании каждого критерия даются формулировки
- 30. Этапы принятия статистического решения 1. Формулировка нулевой
- 31. 5. Вычисление соответствующего эмпирического значения по экспериментальным
- 32. Скачать презентацию
- 33. Похожие презентации
Общие принципы проверки статистических гипотез: Статистические гипотезыУровень статистической значимостиОсь значимости






























Слайд 2
Общие принципы проверки статистических гипотез:
Статистические гипотезы
Уровень статистической
значимости
Слайд 3
Определение. Генеральная совокупность — это вся подлежащая изучению
совокупность объектов или возможных результатов всех мыслимых наблюдений, производимых
в неизменных условиях над одним объектом.
Слайд 4
Определение. Выборкой называется любая подгруппа элементов (испытуемых, респондентов),
выделенная из генеральной совокупности для проведения эксперимента.
Слайд 5 Определение. Выборочное исследование – это исследование, при котором
исследователь (психолог, педагог)
производит выбор ограниченного числа элементов из изучаемой
генеральнойсовокупности.
Слайд 6 Выборки называются независимыми (несвязными), если процедура эксперимента и
полученные результаты измерения некоторого свойства у испытуемых одной выборки
не оказывают влияния на особенности протекания этого же эксперимента и результаты измерения этого же свойства у испытуемых (респондентов) другой выборки.
Слайд 7 Выборки называются зависимыми (связными) если процедура эксперимента
и полученные результаты измерения некоторого свойства, проведенные на одной
выборке, оказывают влияние на другую.
Слайд 8
Требования к выборке:
1. Однородность. Выбор осуществляется на основаниях:
возраст, уровень интеллекта, национальность, заболевания.
2. Репрезентативность. Качество
выборки, позволяющее распространятьполученные на ней выводы на всю генеральную совокупность.
Репрезентативная выборка представляет собой меньшую по размеру, но точную модель той генеральной совокупности, которую она должна отражать.
Слайд 9 Смысл статистических методов заключается в том,
чтобы по выборке ограниченного объема, т.е. по некоторой части
генеральной совокупности, высказать обоснованное суждение об ее свойствах в целом.Слайд 10 Числовые значения, характеризующие генеральную совокупность, называются параметрами.
Одна из задач математической статистики – определение параметров
большого массива по исследованию его части.Слайд 11 В силу действия случайных вероятностных причин оценка
параметров генеральной сово-купности, сделанная на основании экспери-ментальных (выборочных) данных,
всегда будет сопровождаться погрешностью.Подобного рода оценки должны рассматри-ваться как предположительные, а не как окончательные утверждения.
Слайд 12 Предположения о свойствах и параметрах генеральной совокупности получили
название статистических гипотез.
Определение. Статистическая гипотеза
– это научная гипотеза,
допускающаястатистическую проверку;
– это всякое предположение о генеральной совокупности, проверяемое по выборке.
Математическая статистика - это научная дисциплина задачей которой является научно обоснованная проверка статистических гипотез.
Слайд 13
Статистические гипотезы:
Нулевая гипотеза – это
гипотеза об отсутствии различий.
Нулевая гипотеза – это то, что
мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий.Альтернативная гипотеза – это гипотеза о значимости различий.
Альтернативная гипотеза – это то, что мы хотим доказать, поэтому иногда ее называют экспериментальной гипотезой.
Слайд 14
Гипотезы:
Направленные гипотезы:
H0: X1 не превышает X2 ;
H1: X1
превышает X2 .
Ненаправленные гипотезы:
H0: X1 не отличается от X2
;H1: X1 отличается от X2 .
Слайд 15
Определение. Правило, по которому принимается решение принять или
отклонить гипотезу H0 (соответственно: отклонить или принять гипотезу H1
), называется статистическим критерием проверки гипотезы H0 .Статистический критерий подразумевает также метод расчета определенного числа - эмпирического значения критерия (Чэмп).
Слайд 16
Статистическая проверка гипотез, основан-ная на экспериментальных, выборочных данных,
неизбежно связана с риском (вероятностью) принять ложное решение.
Слайд 18
Проблема:
Как определить, где проходит линия между
принятием и отвержением сформулированной исследователем гипотезы?
Слайд 19
Определение. Уровнем значимости называется вероятность ошибочного отклонения нулевой
гипотезы.
Иными словами, уровень значимости это вероятность ошибки первого
рода при принятии решения.(Обозначается: α или Р)
Слайд 20
В прикладных науках, использующих статистику, считается, что
низшим
уровнем статистической значимости является уровень Р=0,05;
достаточным — уровень
Р=0,01 ;высшим – уровень Р=0,001 .
Величины 0,05, 0,01 и 0,001 — это так называемые стандартные уровни статистической значимости.
Слайд 21
Правило принятия статистического вывода
На основании полученных экспериментальных данных
психолог подсчитывает по выбранному им статистическому методу так называемую
эмпирическую статистику, или эмпирическое значение Чэмп .Эмпирическая статистика Чэмп сравнивается с двумя критическими величинами, которые соответствуют уровням значимости в 5% и в 1% для выбранного статистического метода и которые, обозначаются как Чкр1 и Чкр2.
Слайд 22 Величины Чкр1 и Чкр2 находятся для данного статистического
метода по соответствующим таблицам, приведенным в Приложении к любому
учебнику по статистике.Найденные по таблицам величины критических значений представляют в следующей стандартной форме записи:
Слайд 23 Сравнение полученного эмпирического значения с критическими (табличными) значениями
удобно осуществлять с помощью «оси значимости».
Ось значимости» –
это прямая, имеющая три выделенные зоны: зона незначимости, зона неопределенности, зона значимости.
Границами трех зон являются критические значения Чкр1 и Чкр2 для уровней Р = 0,05 и Р = 0,01
Слайд 26 2 случай. Принимается альтернативная гипотеза Н1, о наличии
различий, а гипотеза Но отклоняется
Слайд 28
3 случай. Возможные варианты статистического вывода
В зависимости от
важности решаемой задачи исследователь может:
а) считать полученную статистическую оценку
достоверной на уровне 5%, и принять, тем самым гипотезу Н1 отклонив гипотезу Но;б) считать полученную статистическую оценку недостоверной на уровне 1%, приняв тем самым, гипотезу Но.
Слайд 29
Замечание. При описании каждого критерия даются формулировки гипотез,
которые он помогает проверить, а также указания, при каких
значениях Чэмп стоит принять или отклонить эксперименталь-ную гипотезу
Слайд 30
Этапы принятия статистического решения
1. Формулировка нулевой и альтернативной
гипотез.
2. Определение объема выборки N.
3. Выбор соответствующего уровня значимости
или вероятности отклонения нулевой гипотезы. 4. Выбор статистического метода, который зависит от типа решаемой психологической задачи.
Слайд 31 5. Вычисление соответствующего эмпирического значения по экспериментальным данным,
согласно выбранному статистическому методу.
6. Нахождение по таблице Приложения для
выбранного статистического метода критических значений, соответствующих уровням значимости для Р = 0,05 и для Р =0,01.7. Построение оси значимости и нанесении на нее табличных критических значений и эмпирического значения Чэмп.
8. Формулировка принятия решения (выбор соответствующей гипотезы Но или Н1 ).