- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Развитие творческих способностей учащихся на учебных занятиях
Содержание
- 2. Содержание:Развитие творческих способностей учащихся на учебных занятиях.Развитие
- 3. Развитие творческих способностей учащихся на учебных занятияхРазвитие
- 4. Развитие творческих способностей учащихся, непосредственно связанное с
- 5. Необычная запись, чертеж, схема. В каждый квадрат
- 6. Использование «Математического героя»В урок вводится какой-
- 7. Зашифрованные примеры( достаточно часто встречаются в рабочих
- 8. Творческие работы учащихся . Творческие работы
- 9. ОАВЕСВ1DПравило параллелепипеда Для сложения трех некомпланарных
- 10. ЗадачаАСВМДоказать:Доказательство
- 11. На ребрах АВ, BD и CD
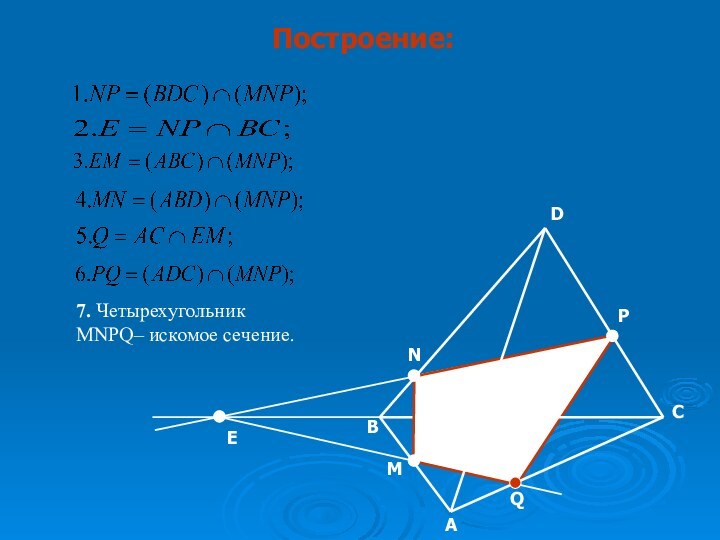
- 12. DCABNPMEQПостроение: 7. Четырехугольник MNPQ– искомое сечение.
- 13. Скачать презентацию
- 14. Похожие презентации
Содержание:Развитие творческих способностей учащихся на учебных занятиях.Развитие творческих способностей во внеклассной работе по предмету.Развитие творческих способностей детей при организации деятельности классного коллектива.









Слайд 2
Содержание:
Развитие творческих способностей учащихся на учебных занятиях.
Развитие творческих
способностей во внеклассной работе по предмету.
при организации деятельности классного коллектива.
Слайд 3
Развитие творческих способностей учащихся на учебных занятиях
Развитие творческих
способностей учащихся, связанное с организацией урока и лишь косвенно
с связанная с учебным материалом:Лучший «решатель» устных упражнений награждается значком «Самый смекалистый».
Фамилии лучших «решателей» заносятся в специальный альбом, один из разделов которого озаглавлен «Смекалистые в нашей школе» (6 классы).
Учащимся, блестяще проявившим себя на уроке, предоставляется право решать задачу из дополнительной литературы к уроку.
Слайд 4 Развитие творческих способностей учащихся, непосредственно связанное с программным
материалом:
Логический каркас. Путем логических рассуждений требуется выявить
из нескольких утверждений одно или несколько верных (неверных). Пример. Из следующих трех равенств только одно верное. 2,7·3,9=105,3; 5,3·9,6=50,88; 4,3·7,3=29,999. Какое? Не торопитесь находить произведение чисел.Провокация ошибки. Построение учебной ситуации таким образом, что ученики, как правило, ошибаются при выполнении какого-либо задания. Например, из чисел 12, 42, 51 и 69 составить несократимую дробь.
«Игра с числами».
Слайд 5
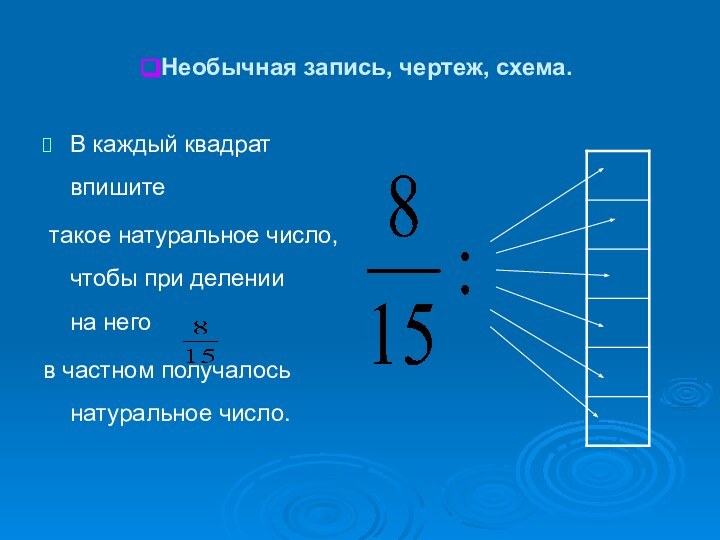
Необычная запись, чертеж, схема.
В каждый квадрат впишите
такое натуральное число, чтобы при делении
на негов частном получалось натуральное число.
Слайд 6
Использование «Математического героя»
В урок вводится какой- либо
герой, который или решает задание, или предлагает его для
решения, или придумывает фокус и т.д.Например, однажды Витя Верхоглядкин записал выражение 25·х·4. Потом стал подставлять в это выражение по очереди числа 13, 21, 39, 47. Получив значение каждого выражения, он очень удивился тому, что все числа оказались «круглыми». Не могли бы вы, ребята, объяснить почему?
Слайд 7
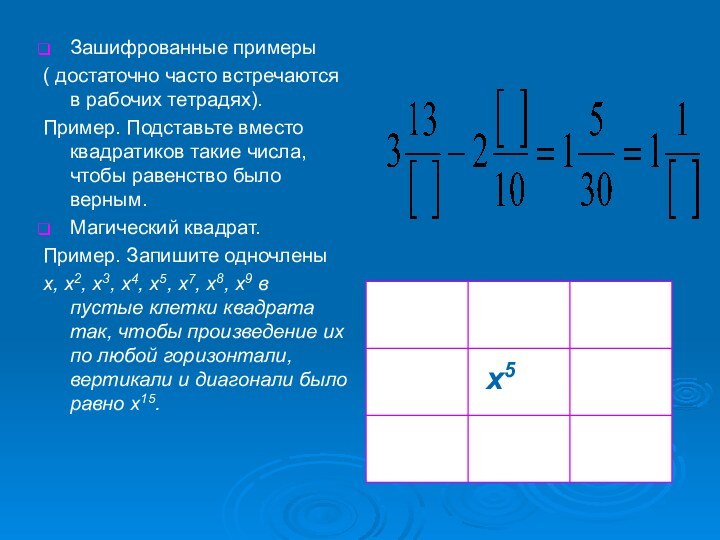
Зашифрованные примеры
( достаточно часто встречаются в рабочих тетрадях).
Пример.
Подставьте вместо квадратиков такие числа, чтобы равенство было верным.
Магический квадрат.
Пример. Запишите одночлены
x, x2, x3, x4, x5, x7, x8, x9 в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x15.
x5
Слайд 8
Творческие работы учащихся .
Творческие работы учащиеся
выполняют по различным разделам курса математики.
В 5 – 6
классах это мини – сочинения «Математика в профессии моих родителей», практические работы .В 10 – 11 классах – зачетные и практические работы по геометрии с применением компьютерных технологий позволяют не только добиться осознанного восприятия учебного материала, но и решают проблему развития творческих способностей детей. Далее предлагаются фрагменты работ учащихся 11б класса.
Слайд 9
О
А
В
Е
С
В1
D
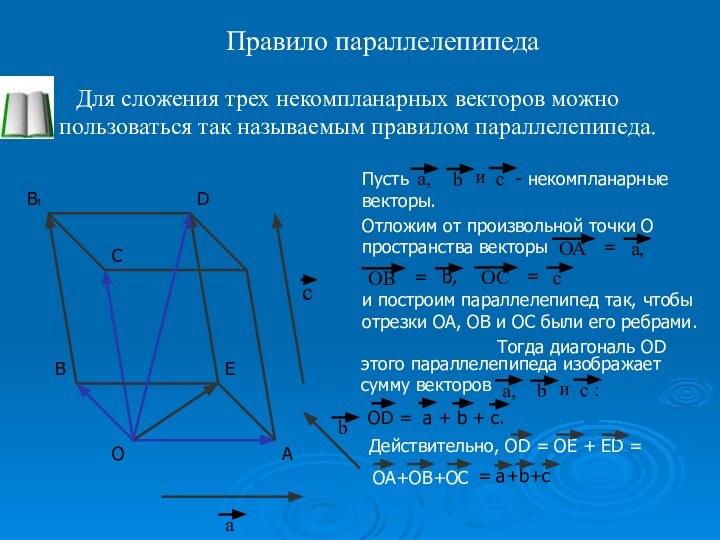
Правило параллелепипеда
Для сложения трех некомпланарных векторов
можно пользоваться так называемым правилом параллелепипеда.
Пусть
- некомпланарные векторы. Отложим от произвольной точки О пространства векторы
и построим параллелепипед так, чтобы отрезки OA, OB и ОС были его ребрами.
Тогда диагональ ОD
этого параллелепипеда изображает сумму векторов
OD = a + b + c.
Действительно, OD = OE + ED =
OA+OB+OC
= a+b+c
Слайд 11 На ребрах АВ, BD и CD тетраэдра
ABCD отмечены точки M, N и Р.
Построить сечение тетраэдра
плоскостью MNP. Задача.