- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Объём призмы
Содержание
- 2. ОБЪЁМ ПРИЗМЫ.ПЛАН ТЕМЫ:I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы.
- 3. Объем каждого тела выражается положительным числом, которое
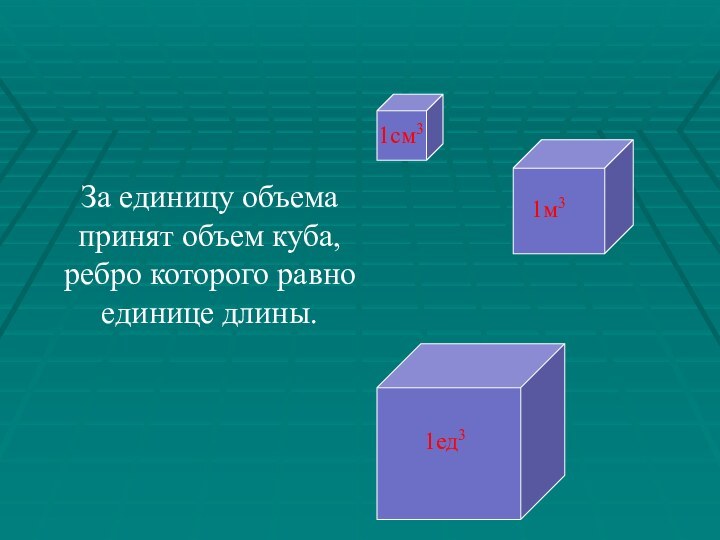
- 4. За единицу объема принят объем куба, ребро которого равно единице длины.1см31м31ед3
- 5. Чтобы найти объём многогранника, нужно разбить его на кубы с ребром, равным единице измерения.V=12ед.3
- 6. Общие свойства объемов тел: I.
- 7. Равные тела имеют равные объемы, при перемещении тела его объем не изменяется; Рассмотрим первое свойство.V1V2V1= V2
- 8. Рассмотрим второе свойство.Если тело разбить на части,
- 9. саbV=abcФормула объёма прямоугольного параллелепипеда.
- 10. Объем прямой треугольной призмы, в основании которой лежит прямоугольный треугольник, равен произведению площади основания на высоту.V=abcV=abc:2:2
- 11. Рассмотрим произвольную прямую треугольную призму ABCA1B1C1. Если
- 12. По свойству объемов, сложив объемы этих треугольных
- 13. Скачать презентацию
- 14. Похожие презентации
ОБЪЁМ ПРИЗМЫ.ПЛАН ТЕМЫ:I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы.











Слайд 3 Объем каждого тела выражается положительным числом, которое показывает,
сколько единиц измерения объемов и частей единицы содержится в
данном теле.Понятие объема
Слайд 5 Чтобы найти объём многогранника, нужно разбить его на
кубы с ребром, равным единице измерения.
V=12ед.3
Слайд 6
Общие свойства объемов тел:
I.
Равные тела имеют равные объемы, при перемещении тела его
объем не изменяется.II. Если тело разбить на части, являющиеся простыми телами, то объем тела равен сумме объемов этих частей.
Слайд 7 Равные тела имеют равные объемы, при перемещении тела
его объем не изменяется;
Рассмотрим первое свойство.
V1
V2
V1= V2
Слайд 8
Рассмотрим второе свойство.
Если тело разбить на части, являющиеся
простыми телами, то объем тела равен сумме объемов всех
частей.Слайд 10 Объем прямой треугольной призмы, в основании которой лежит
прямоугольный треугольник, равен произведению площади основания на высоту.
V=abc
V=abc
:2
:2
Слайд 11 Рассмотрим произвольную прямую треугольную призму ABCA1B1C1. Если DABC
не прямоугольный, то его можно разбить на два прямоугольных
треугольника ADC и BDC.A D B
A1 D1 B1
C1
C
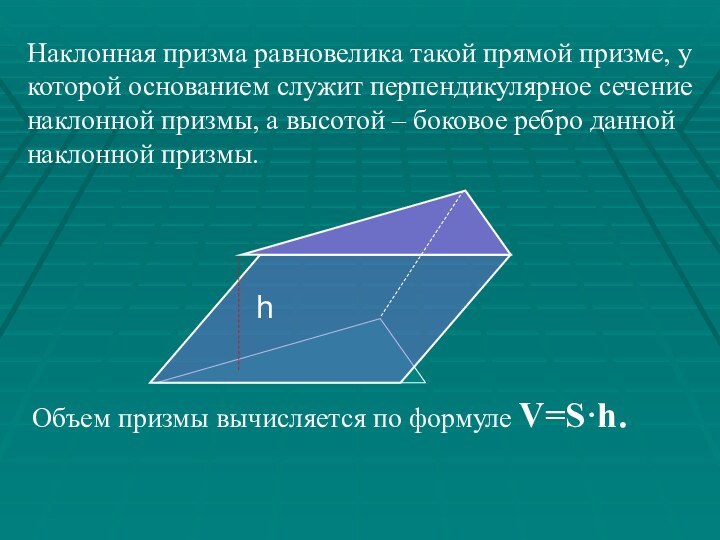
Как же найти объём произвольной призмы?
V=S·h
S- площадь основания; ·h-высота призмы
Слайд 12 По свойству объемов, сложив объемы этих треугольных призм,
получим объем данной.
Ф1
Ф2
Ф3
V=V1 +V2 +V3
Пусть дана n –
угольная прямая призма (n>3).Разобьем ее на конечное число прямых треугольных призм.
V=S1·h+S2·h+S3·h
V=S·h





























