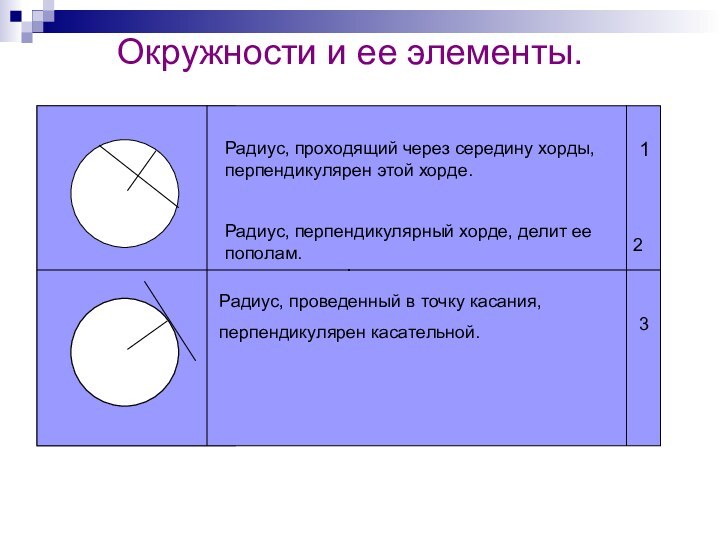
хорды, перпендикулярен этой хорде.
Радиус, перпендикулярный хорде, делит ее пополам.
Радиус,
проведенный в точку касания, перпендикулярен касательной.
1
3
2
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Окружности
Содержание
- 2. Окружности и ее элементы. .Радиус, проходящий через
- 3. Отрезки касательных, проведенных из однойточки, равны.Центр окружности
- 4. Вписанные углы, опирающиеся на одну дугу,равны.Вписанные угол,
- 5. Окружность, вписанная в треугольник.Отрезок, соединяющий центр окружностии
- 6. Окружность, описанная около треугольникаЦентр описанной окружности лежит
- 7. пример1Из точки А к окружности с центром
- 8. Скачать презентацию
- 9. Похожие презентации
Окружности и ее элементы. .Радиус, проходящий через середину хорды, перпендикулярен этой хорде.Радиус, перпендикулярный хорде, делит ее пополам.Радиус, проведенный в точку касания, перпендикулярен касательной.132
Слайд 2
Окружности и ее элементы.
.
Радиус, проходящий через середину
хорды, перпендикулярен этой хорде.
проведенный в точку касания, перпендикулярен касательной.
Слайд 3
Отрезки касательных, проведенных из одной
точки, равны.
Центр окружности лежит
на биссектрисе угла,
образованного касательными, проведенными из одной точки.
Градусная мера
центрального угла равнаградусной мере дуги, на которую он опирается.
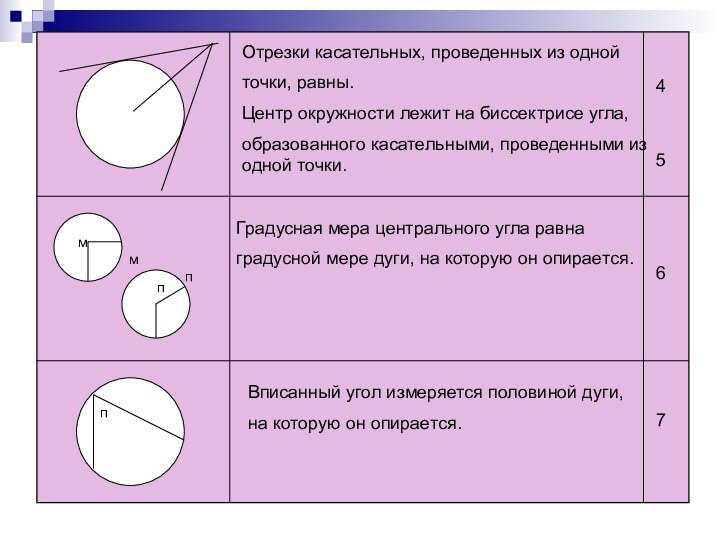
Вписанный угол измеряется половиной дуги,
на которую он опирается.
п
п
п
м
м
4
5
6
7
Слайд 4
Вписанные углы, опирающиеся на одну дугу,
равны.
Вписанные угол, опирающийся
на диаметр,
равен 90градусав.
Если две хорды окружности пересекаются, то
произведение отрезков
одной хорды равнопроизведению отрезков другой хорды:
AxD=MxH
М
D
H
A
8
9
10
Слайд 5
Окружность, вписанная в треугольник.
Отрезок, соединяющий центр окружности
и точку
ее касания со стороной,
перпендикулярен этой стороне.
Отрезки двух соседних сторон
от общейвершине до точек касания равны между собой.
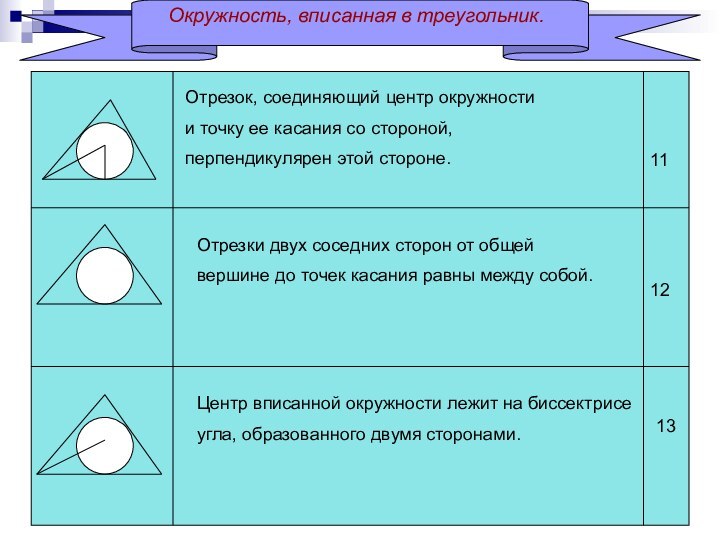
Центр вписанной окружности лежит на биссектрисе
угла, образованного двумя сторонами.
11
12
13
Слайд 6
Окружность, описанная около треугольника
Центр описанной окружности лежит на
серединном перпендикуляре к любой из сторон треугольника.
Если прямоугольный треугольник
вписан вОкружность, то его гипотенуза является диаметром
Окружности.
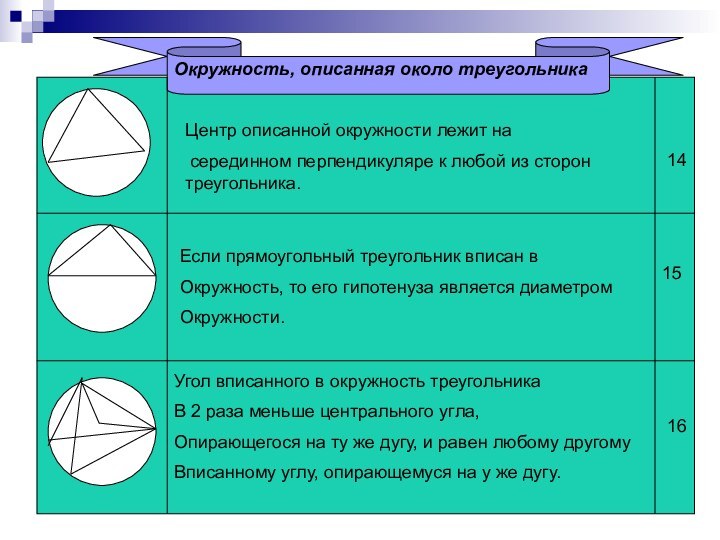
Угол вписанного в окружность треугольника
В 2 раза меньше центрального угла,
Опирающегося на ту же дугу, и равен любому другому
Вписанному углу, опирающемуся на у же дугу.
14
15
16
Слайд 7
пример
1
Из точки А к окружности с центром О
проведены касательные АВ с АС. Отрезки АО
и ВС пересекаются в точке К. Найдите радиус окружности, если ВС=6, АК=2,25.О
В
С
А
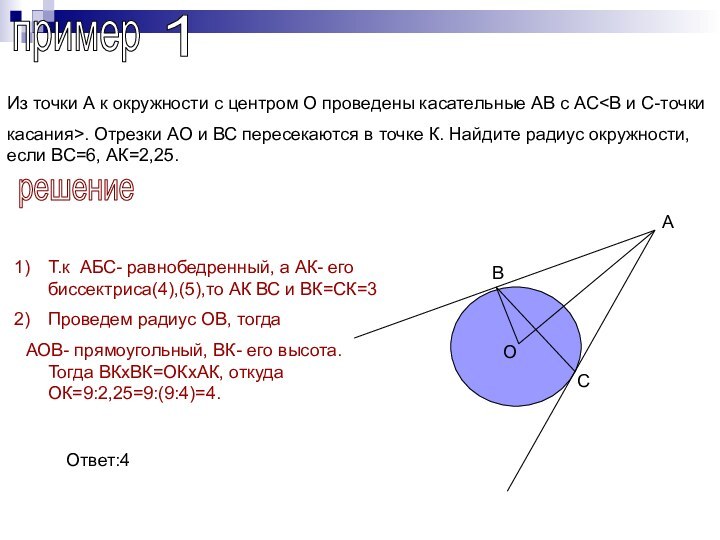
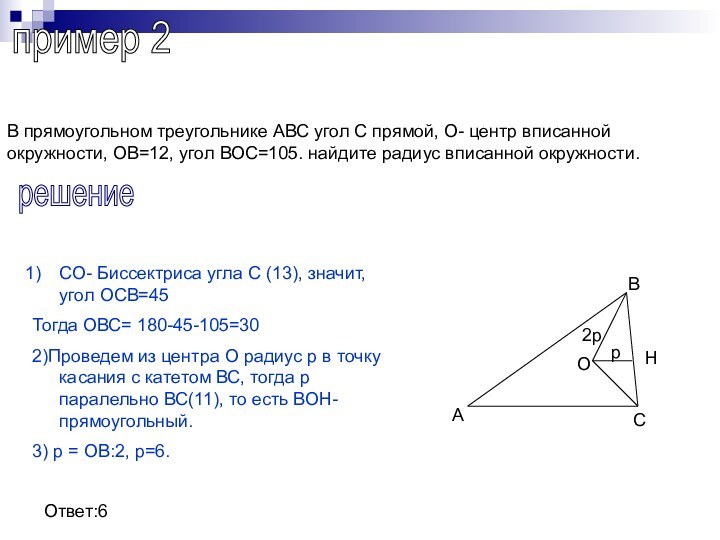
решение
Т.к АБС- равнобедренный, а АК- его биссектриса(4),(5),то АК ВС и ВК=СК=3
Проведем радиус ОВ, тогда
АОВ- прямоугольный, ВК- его высота. Тогда ВКxВК=ОКxАК, откуда ОК=9:2,25=9:(9:4)=4.
Ответ:4
