двести с лишним лет назад. Одной из таких задач-головоломок
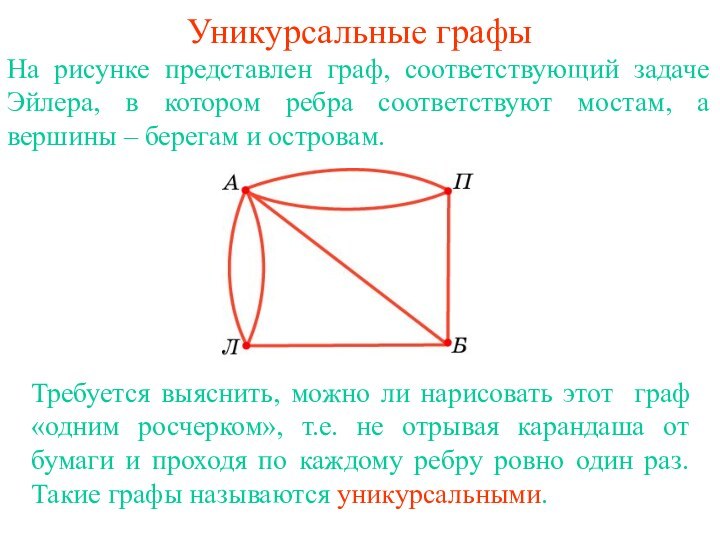
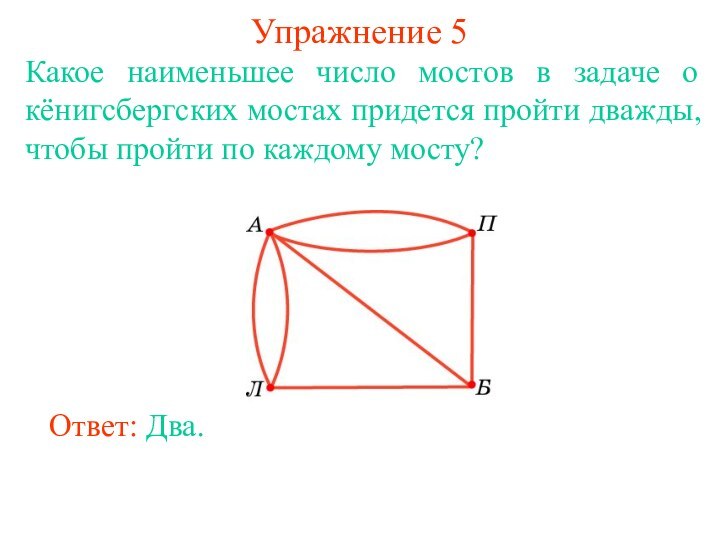
была задача о кенигсбергских мостах, которая привлекла к себе внимание Леонарда Эйлера (1707-1783), долгое время жившего и работавшего в России (с 1727 по 1741 год и с 1766 до конца жизни).Задача. В г. Кёнигсберге (ныне Калининград) было семь мостов через реку Прегель (Л - левый берег, П - правый берег, А и Б - острова). Можно ли, прогуливаясь вдоль реки, пройти по каждому мосту ровно один раз?