Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Перпендикулярность прямых и плоскостей

Содержание

2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПЕРПЕНДИКУЛЯР И НАКЛОННАЯТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДВУГРАННЫЙ УГОЛРЕШЕНИЕ ЗАДАЧПлан:
3. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПрямая называется перпендикулярной плоскости,
4. Докажите, что плоскость, проходящая через ребро AB
5. Докажите, что прямая AA1, проходящая через вершины
6. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯПусть дана плоскость π и
7. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯНаклонной к плоскости называется прямая,
8. Дано:αАС ⊥ α; С ∈ α АВ
9. Установить взаимное положение прямых а и в
10. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДве плоскости называются перпендикулярными, если угол
11. б) AВB1, CDD1, AB1C1.В кубе A…D1 укажите
12. ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1),
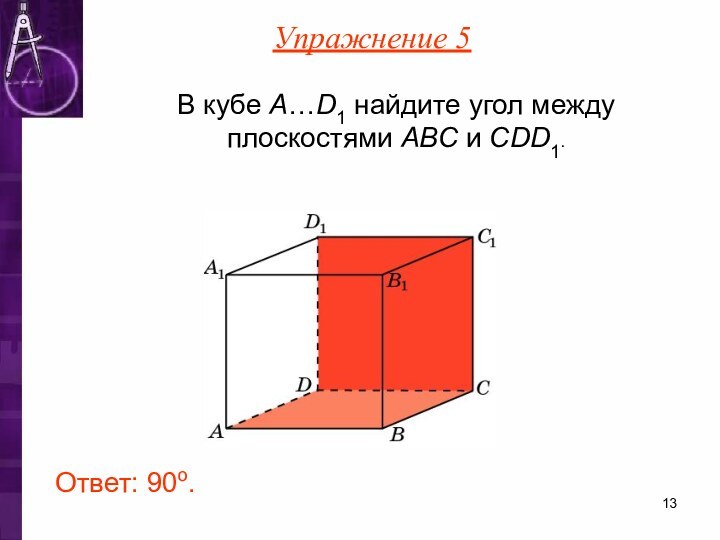
13. В кубе A…D1 найдите угол между плоскостями ABC и CDD1.Ответ: 90o.Упражнение 5
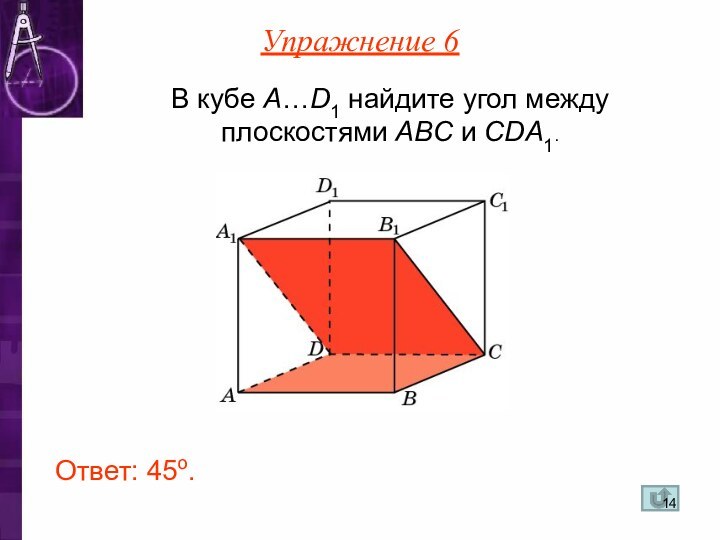
14. В кубе A…D1 найдите угол между плоскостями ABC и CDA1.Ответ: 45o.Упражнение 6
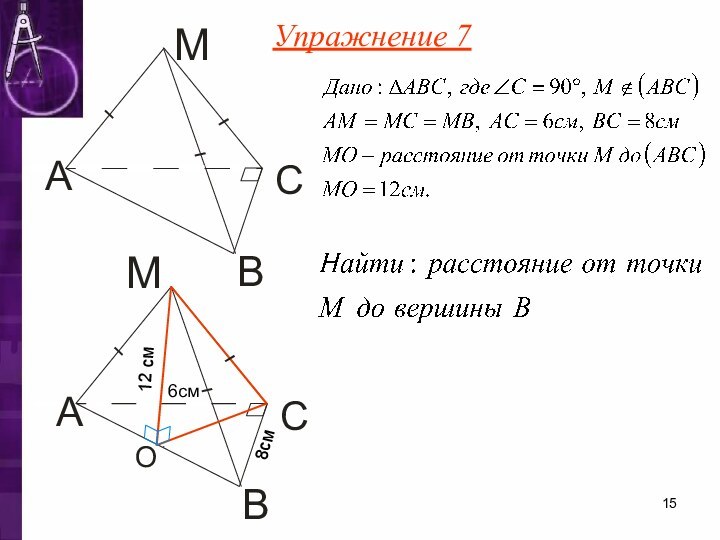
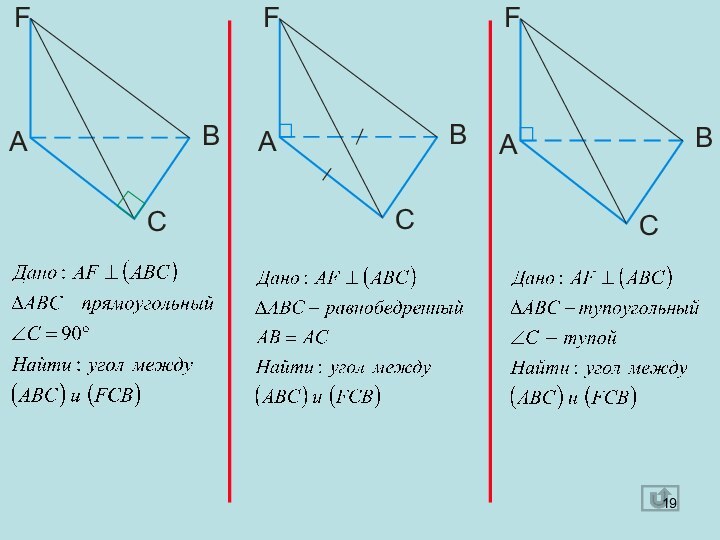
15. Упражнение 7
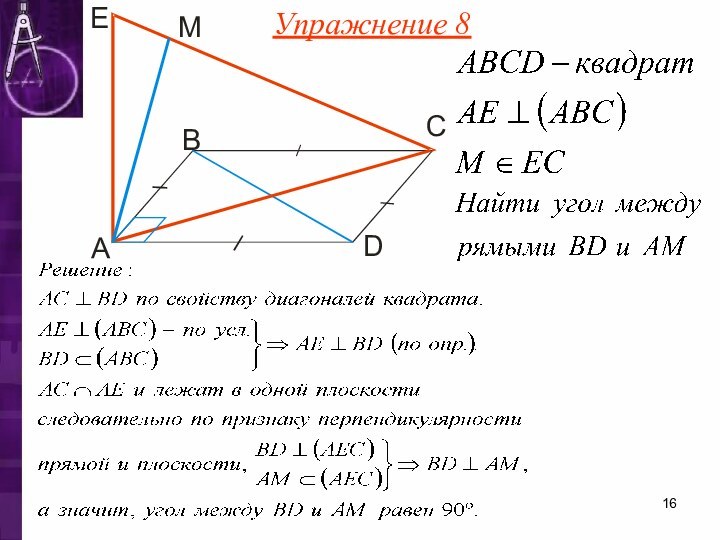
16. Упражнение 8
17. Точка М равноудалена от всех вершин правильного
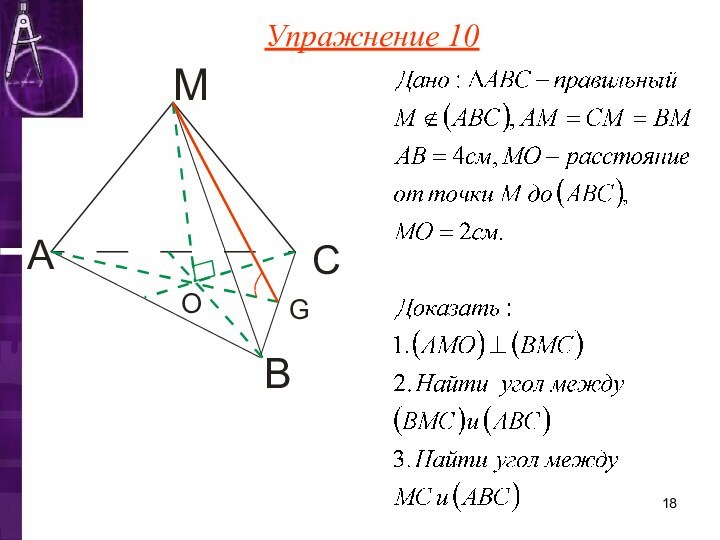
18. Упражнение 10
19. Скачать презентацию
20. Похожие презентации

ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПЕРПЕНДИКУЛЯР И НАКЛОННАЯТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДВУГРАННЫЙ УГОЛРЕШЕНИЕ ЗАДАЧПлан:

Главная
Математика
Перпендикулярность прямых и плоскостей

«Перпендикулярность прямых и плоскостей»

ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПЕРПЕНДИКУЛЯР И НАКЛОННАЯТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДВУГРАННЫЙ УГОЛРЕШЕНИЕ ЗАДАЧПлан:

ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПрямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой,

Докажите, что плоскость, проходящая через ребро AB правильного тетраэдра ABCD и точку

Докажите, что прямая AA1, проходящая через вершины куба ABCDA1B1C1D1 перпендикулярна плоскости ABC.Доказательство.

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯПусть дана плоскость π и точка A пространства. Через точку

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯНаклонной к плоскости называется прямая, пересекающая эту плоскость и не

Дано:αАС ⊥ α; С ∈ α АВ - наклоннаяВС - проекцияa ⊂

Установить взаимное положение прямых а и в по готовым чертежам Задача1. ABCD

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДве плоскости называются перпендикулярными, если угол между ними прямой.Теорема. (Признак перпендикулярности

б) AВB1, CDD1, AB1C1.В кубе A…D1 укажите плоскости, проходящие через вершины куба,

ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1), образованная двумя полуплоскостями, с общей

В кубе A…D1 найдите угол между плоскостями ABC и CDD1.Ответ: 90o.Упражнение 5

В кубе A…D1 найдите угол между плоскостями ABC и CDA1.Ответ: 45o.Упражнение 6

Точка М равноудалена от всех вершин правильного треугольника ABC, сторона которого равна

Слайды презентации

Слайд 2 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
ТЕОРЕМА О ТРЕХ

ПЕРПЕНДИКУЛЯРАХ
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
ДВУГРАННЫЙ УГОЛ
РЕШЕНИЕ ЗАДАЧ
План:

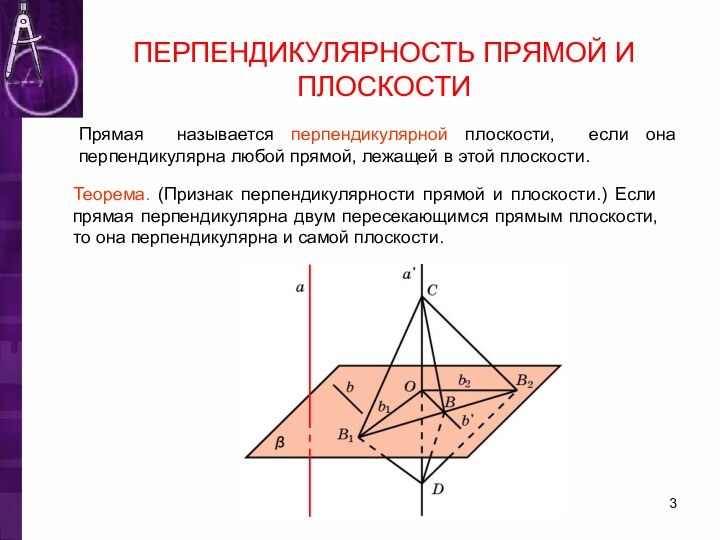
Слайд 3 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая называется перпендикулярной плоскости, если

ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПрямая называется перпендикулярной плоскости, если она перпендикулярна любой

она перпендикулярна любой прямой, лежащей в этой плоскости.
Теорема. (Признак

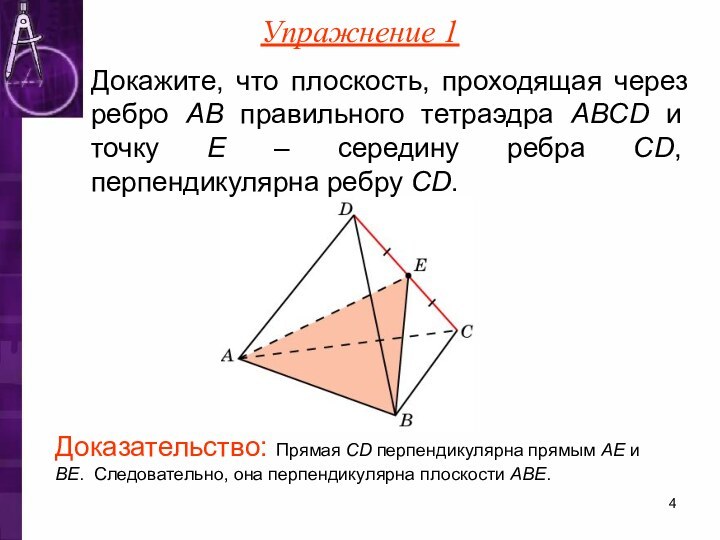
перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости.

Слайд 4 Докажите, что плоскость, проходящая через ребро AB правильного

Докажите, что плоскость, проходящая через ребро AB правильного тетраэдра ABCD и

тетраэдра ABCD и точку Е – середину ребра CD,

перпендикулярна ребру CD.

Упражнение 1

Доказательство: Прямая CD перпендикулярна прямым AE и BE. Следовательно, она перпендикулярна плоскости ABE.

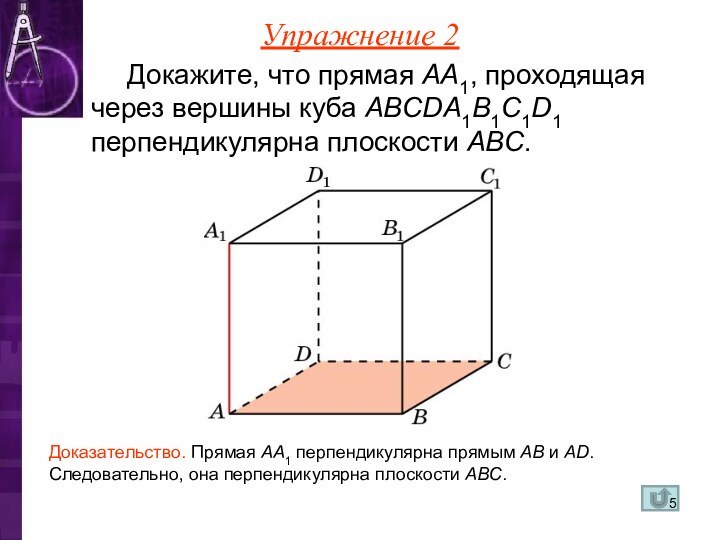
Слайд 5 Докажите, что прямая AA1, проходящая через вершины куба

Докажите, что прямая AA1, проходящая через вершины куба ABCDA1B1C1D1 перпендикулярна плоскости

ABCDA1B1C1D1 перпендикулярна плоскости ABC.
Доказательство. Прямая AA1 перпендикулярна прямым AB

и AD. Следовательно, она перпендикулярна плоскости ABC.

Упражнение 2

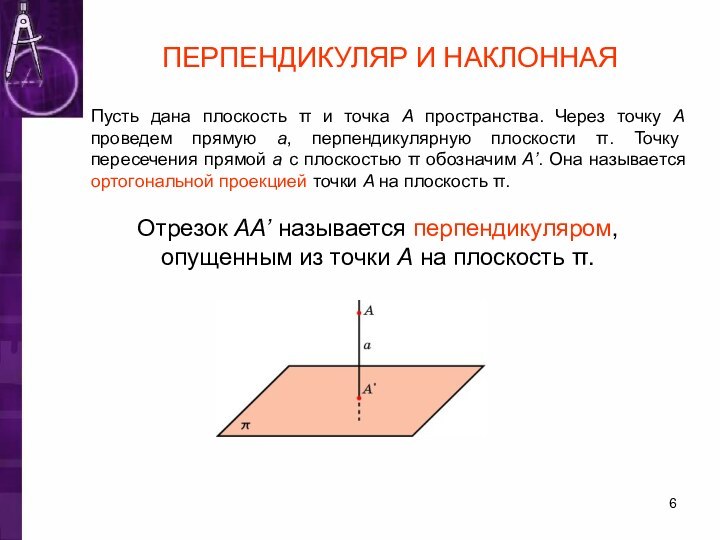
Слайд 6 ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Пусть дана плоскость π и точка

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯПусть дана плоскость π и точка A пространства. Через

A пространства. Через точку A проведем прямую a, перпендикулярную

плоскости π. Точку пересечения прямой a с плоскостью π обозначим A’. Она называется ортогональной проекцией точки A на плоскость π.

Отрезок AA’ называется перпендикуляром, опущенным из точки A на плоскость π.

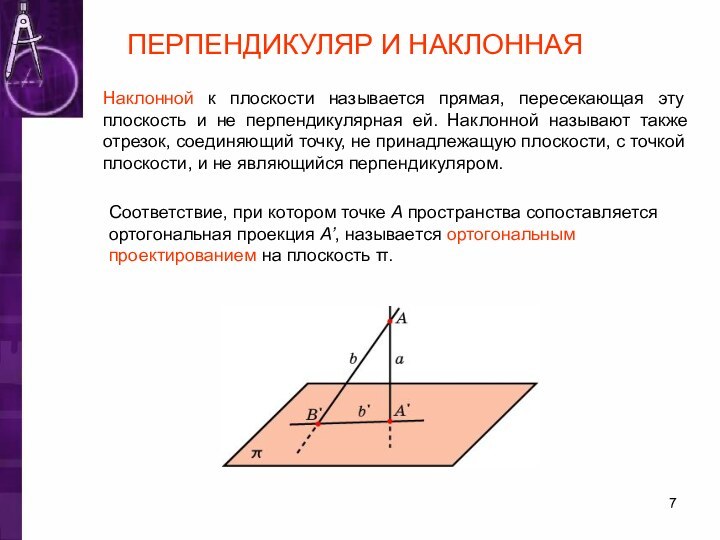
Слайд 7 ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Наклонной к плоскости называется прямая, пересекающая

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯНаклонной к плоскости называется прямая, пересекающая эту плоскость и

эту плоскость и не перпендикулярная ей. Наклонной называют также

отрезок, соединяющий точку, не принадлежащую плоскости, с точкой плоскости, и не являющийся перпендикуляром.

Соответствие, при котором точке A пространства сопоставляется ортогональная проекция A’, называется ортогональным проектированием на плоскость π.

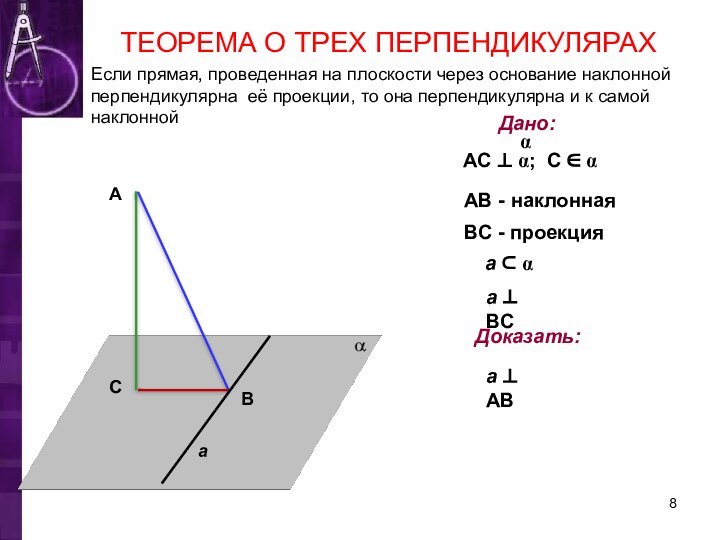
Слайд 8 Дано:
α
АС ⊥ α; С ∈ α
АВ -

наклонная
ВС - проекция
a ⊂ α
a ⊥ ВС
Доказать:
a ⊥ АВ

ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Если прямая, проведенная на плоскости через основание наклонной перпендикулярна её проекции, то она перпендикулярна и к самой наклонной

Слайд 9
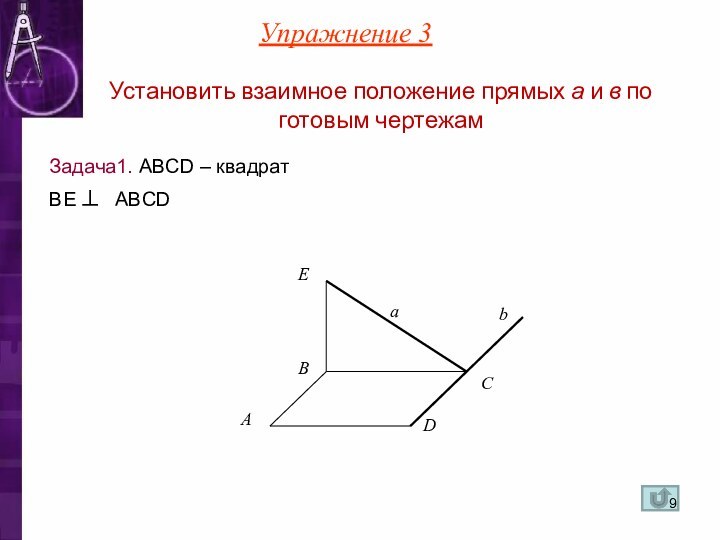
Установить взаимное положение прямых а и в по

Установить взаимное положение прямых а и в по готовым чертежам Задача1.

готовым чертежам
Задача1. ABCD – квадрат
BE ⊥ ABCD

Упражнение 3

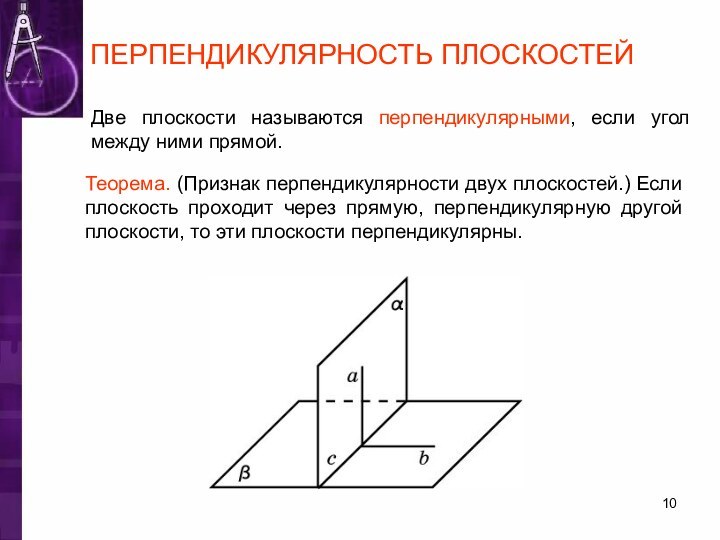
Слайд 10 ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Две плоскости называются перпендикулярными, если угол между

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДве плоскости называются перпендикулярными, если угол между ними прямой.Теорема. (Признак

ними прямой.
Теорема. (Признак перпендикулярности двух плоскостей.) Если плоскость проходит

через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

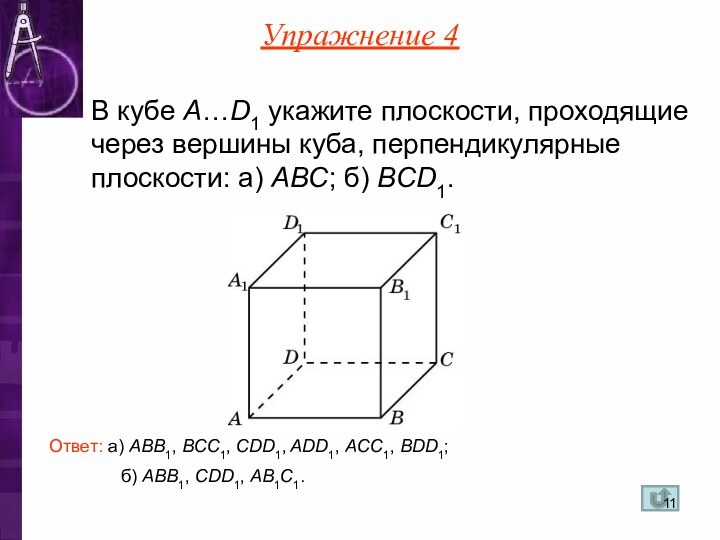
Слайд 11 б) AВB1, CDD1, AB1C1.
В кубе A…D1 укажите плоскости,

б) AВB1, CDD1, AB1C1.В кубе A…D1 укажите плоскости, проходящие через вершины

проходящие через вершины куба, перпендикулярные плоскости: а) ABC; б)

BCD1.

Ответ: а) ABB1, BCC1, CDD1, ADD1, ACC1, BDD1;

Упражнение 4

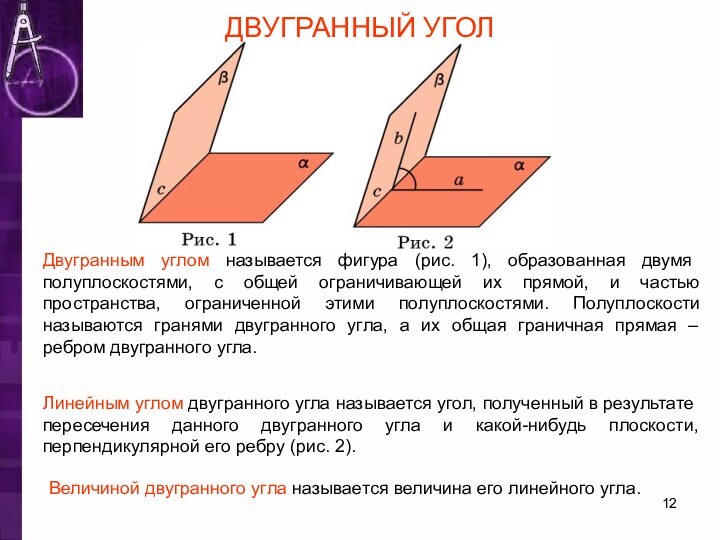
Слайд 12 ДВУГРАННЫЙ УГОЛ
Двугранным углом называется фигура (рис. 1), образованная

ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1), образованная двумя полуплоскостями, с

двумя полуплоскостями, с общей ограничивающей их прямой, и частью

пространства, ограниченной этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла.

Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).

Величиной двугранного угла называется величина его линейного угла.

Слайд 13 В кубе A…D1 найдите угол между плоскостями ABC

и CDD1.
Ответ: 90o.
Упражнение 5

Слайд 14 В кубе A…D1 найдите угол между плоскостями ABC

и CDA1.
Ответ: 45o.
Упражнение 6

Слайд 15 Упражнение 7

Слайд 16 Упражнение 8

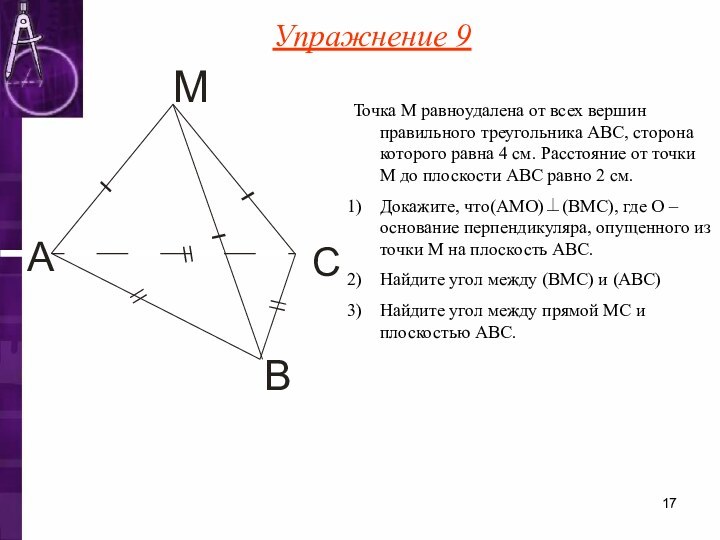
Слайд 17 Точка М равноудалена от всех вершин правильного треугольника

Точка М равноудалена от всех вершин правильного треугольника ABC, сторона которого

ABC, сторона которого равна 4 см. Расстояние от точки

М до плоскости ABC равно 2 см.
Докажите, что(AMO)⊥(BMC), где O – основание перпендикуляра, опущенного из точки М на плоскость ABC.
Найдите угол между (BMC) и (ABC)
Найдите угол между прямой MC и плоскостью ABC.

Упражнение 9