- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определение логарифма. Основное логарифмическое тождество
Содержание
- 2. «Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней словно удваивает жизнь астрономов»П.С. Лаплас
- 3. ЦЕЛЬ УРОКАПознакомиться с понятием логарифма, основным логарифмическим тождеством, научиться применять их на практике.
- 4. ПОВТОРЕНИЕПоказательная функция, показательные уравнения и неравенства.Устно: anОснование степениПоказатель
- 5. х = ?
- 6. ОПРЕДЕЛЕНИЕЛогарифмом по основанию а от аргумента x
- 7. ЛОГАРИФМИРОВАНИЕЭТО ОПЕРАЦИЯ НАХОЖДЕНИЯ ЛОГАРИФМА ПО ЗАДАННОМУ ОСНОВАНИЮlog2 5 = 2,321928…
- 8. ВАЖНЫЕ ФАКТЫ:1.Аргумент и основание логарифма всегда должны быть
- 9. ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВОРавенство справедливо при b > 0, a > 0, a ≠ 152
- 10. ТРИ ФОРМУЛЫ:
- 11. На протяжении 16 века быстро возрастало количество
- 12. Логарифмы были придуманы для ускорения и упрощения
- 13. состоит в сведении сложных действий возведения в
- 14. ДОКАЗАТЕЛЬСТВО:
- 15. ВЫЧИСЛИТЕ: №267-270(нч)ПРОВЕРКА:
- 16. ВЫЧИСЛИТЕ: №274-276(нч)ПРОВЕРКА:
- 17. ВЫЯСНИТЕ ПРИ КАКИХ ЗНАЧЕНИЯХ Х СУЩЕСТВУЕТ ЛОГАРИФМ: № 278(НЧ)ПРОВЕРКА:Нет таких х.
- 18. ОКАЗЫВАЕТСЯ…математическим символом соотношения формы и роста является логарифмическая спиральраковина моллюскарога горных барановсемена подсолнечника
- 19. По логарифмическим спиралям закручены и многие галактики, в том числе и Галактика, которой принадлежит Солнечная система.ОКАЗЫВАЕТСЯ…
- 20. ДОМАШНЕЕ ЗАДАНИЕ:1.Параграф 15 – выучить определение логарифма.2.Решить
- 21. Скачать презентацию
- 22. Похожие презентации



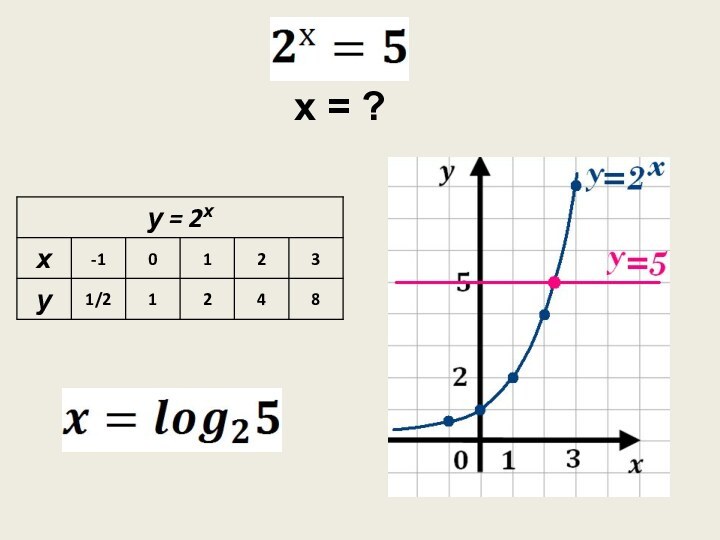
















Слайд 2 «Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд
нескольких дней словно удваивает жизнь астрономов»
Слайд 3
ЦЕЛЬ УРОКА
Познакомиться с понятием логарифма,
основным логарифмическим тождеством,
научиться применять их на практике.
Слайд 4
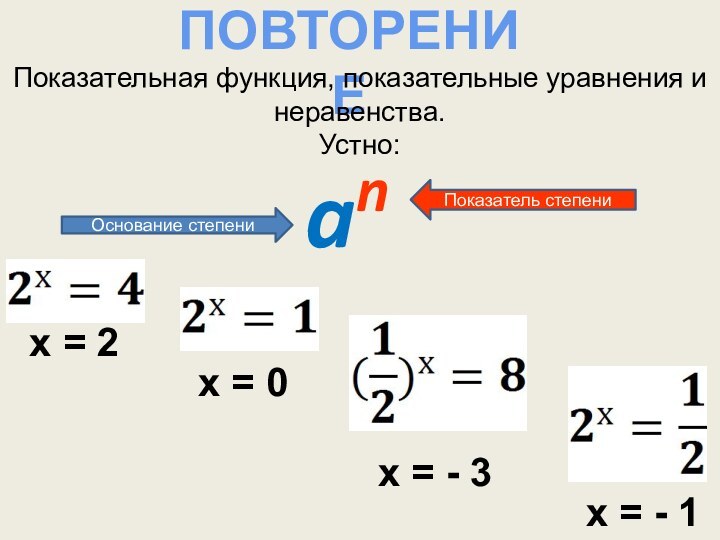
ПОВТОРЕНИЕ
Показательная функция, показательные уравнения и неравенства.
Устно:
an
Основание степени
Показатель степени
х
= 2
х = - 3
х = 0
х = -
1
Слайд 6
ОПРЕДЕЛЕНИЕ
Логарифмом по основанию а от аргумента x называют
степень, в которую нужно возвести а, чтобы получить х.
logax
= bГде:
а – основание логарифма;
х – аргумент (число или выражение под знаком логарифма);
b – значение логарифма.
Например:
log28 = 3
(логарифм по основанию 2 от числа 8 равен 3, поскольку 23 = 8 )
Слайд 7
ЛОГАРИФМИРОВАНИЕ
ЭТО ОПЕРАЦИЯ НАХОЖДЕНИЯ ЛОГАРИФМА ПО ЗАДАННОМУ ОСНОВАНИЮ
log2 5 = 2,321928… -
иррациональное число
2 ≤ log2 5 ≤ 3,так как 22
5 < 23Если логарифм получается иррациональным, его лучше так и оставить:
log2 5, log3 7, log5 2 и другие
Слайд 8
ВАЖНЫЕ ФАКТЫ:
1.Аргумент и основание логарифма всегда должны быть больше нуля.
Это следует из определения степени с рациональным показателем, к которому сводится
определение логарифма.
2.Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей.
loga x = b ⇒ x > 0, a > 0, a ≠ 1.
3.На число b (значение логарифма) никаких ограничений не накладывается.
Слайд 11 На протяжении 16 века быстро возрастало количество приближенных
вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных
движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.Проблемы возникали и в других областях, например, в финансовом и страховом деле нужны были таблицы сложных процентов для различных значений процента.
Главную трудность представляли умножение, деление многозначных чисел.
ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 12
Логарифмы были придуманы для ускорения и упрощения вычислений.
Идея
логарифма, т. е. идея выражать числа в виде степени одного
и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития.Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632).
В1614г. была опубликована работа Непера под названием «Описание удивительной таблицы логарифмов»
Слово «логарифм» введено Непером, происходит от греческих слов logoz и ariumoz - оно означает буквально “числа отношений”.
ИСТОРИЧЕСКАЯ СПРАВКА
Джон Непер
Слайд 13 состоит в сведении сложных действий возведения в степень
и извлечения корня к более простым действиям - умножению
и делению, а последних к - самым простым – сложению и вычитанию.Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов упростило жизнь тех, кто по роду своей деятельности был связан с громоздкими вычислениями и сложными расчетами.
ЦЕННОСТЬ ЛОГАРИФМОВ
Логарифмическая линейка
Палочки Непера
Слайд 18
ОКАЗЫВАЕТСЯ…
математическим символом соотношения формы и роста является логарифмическая
спираль
раковина моллюска
рога горных баранов
семена подсолнечника
Слайд 19 По логарифмическим спиралям закручены и многие галактики, в
том числе и Галактика, которой принадлежит Солнечная система.
ОКАЗЫВАЕТСЯ…
Слайд 20
ДОМАШНЕЕ ЗАДАНИЕ:
1.Параграф 15 – выучить определение логарифма.
2.Решить в
тетрадях для домашних работ:
- первый уровень -
№271-273(четные), №283(2).- второй уровень - №279-281(четные), №284(четные).





























