Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Определение вектора в пространстве

Содержание

Содержание I. Понятие вектора в пространствеII. Коллинеарные векторыIII. Компланарные векторыIV. Действия с векторамиV. Разложение вектораVI. Базисные задачиПроверь себяОб авторе Помощь в управлении презентациейВыход
Векторы в пространствевход Содержание I. Понятие вектора в пространствеII. Коллинеарные векторыIII. Компланарные векторыIV. Действия с векторамиV. Разложение вектораVI. Базисные задачиПроверь себяОб Понятие вектора в пространствеВектор(направленный отрезок) – отрезок, для которого указано какой из Коллинеарные векторыДва ненулевых вектора называются коллинеарными, если они лежат на одной прямой Сонаправленные векторыСонаправленные векторы - векторы, лежащие по одну сторону от прямой, проходящей Равные векторыРавные векторы - сонаправленные векторы, длины которых равны.От любой точки можно Противоположно направленные векторыПротивоположно направленные векторы – векторы, лежащие по разные стороны от Противоположные векторыПротивоположные векторы – противоположно направленные векторы, длины которых равны.Вектором, противоположным нулевому, считается нулевой вектор. Признак коллинеарностиДоказательство Доказательство признака коллинеарности Определение компланарных векторовКомпланарные векторы – векторы, при откладывании которых от одной и О компланарных векторахЛюбые два вектора всегда компланарны.Три вектора, среди которых имеются два коллинеарных, компланарны.αесли Признак компланарностиДоказательствоЗадачи Задачи на компланарностьКомпланарны ли векторы: а) б) Справка РешениеИзвестно, что векторы , Решение Решение Решение Доказательство признака компланарностиСOA1B1BA Свойство компланарных векторов Действия с векторамиСложениеВычитаниеУмножение вектора на числоСкалярное произведение Сложение векторовПравило треугольникаПравило параллелограммаПравило многоугольникаПравило параллелепипедаСвойства сложения Правило треугольникаАBC Правило треугольникаАBCДля любых трех точек А, В и С справедливо равенство: Правило параллелограммаАBC Свойства сложения 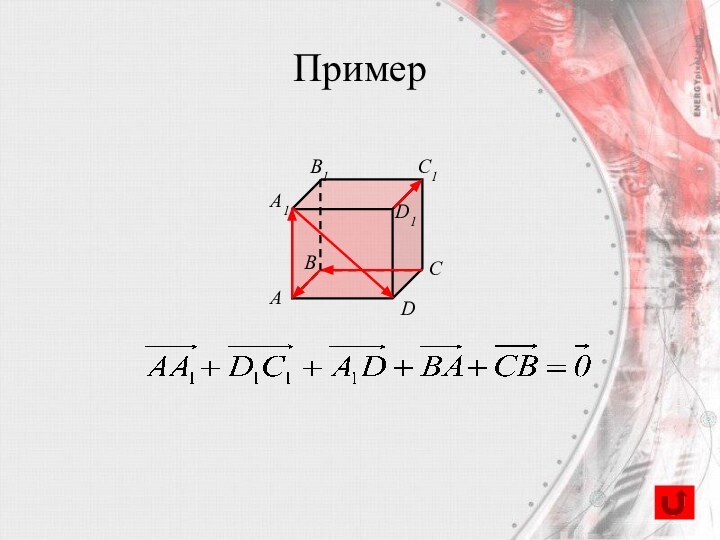Правило многоугольникаСумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при последовательном откладывании).BACDEПример ПримерCABDA1B1C1D1 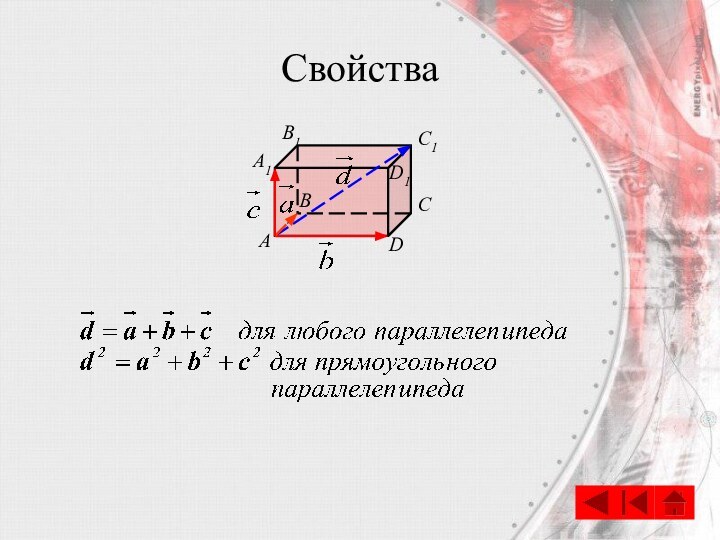Правило параллелепипедаBАCDA1B1C1D1Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той СвойстваBАCDA1B1C1D1 Вычитание векторовВычитаниеСложение с противоположным ВычитаниеРазностью векторов и называется такойвектор, сумма которого с ВычитаниеBAПравило трех точек C Правило трех точекЛюбой вектор можно представить как разность двух векторов, проведенных из одной точки.АBK Сложение с противоположнымРазность векторов и можно Умножение вектора на число СвойстваПроизведением нулевого вектора на любое число считается нулевой вектор.Произведение любого вектора на Свойства Скалярное произведениеСкалярным произведением двух векторов называется произведение их длин на косинус угла Справедливые утверждения скалярное произведение ненулевых векторов равно нулю тогда и только тогда, Вычисление скалярного произведения в координатахДоказательство Доказательство формулы скалярного произведенияOABαOBAOBA Доказательство формулы скалярного произведения Свойства скалярного произведения10.20.30.40.(переместительный закон)(распределительный закон)(сочетательный закон) Разложение вектораПо двум неколлинеарным векторамПо трем некомпланарным векторам Разложение вектора по двум неколлинеарным векторамТеорема. Любой вектор можно разложить по двум Доказательство теоремыOAA1BPПусть коллинеарен .Тогда не коллинеарен ни вектору , ни вектору Доказательство теоремыДокажем, что коэффициенты разложения определяются единственным образом.Допустим:Тогда:- Разложение вектора по трем некомпланарным векторамЕсли вектор p представлен в видегде x, Доказательство теоремыСOABP1P2P Доказательство теоремыДокажем, что коэффициенты разложения определяются единственным образом.Допустим:Тогда:- Базисные задачиВектор, проведенный в середину отрезкаВектор, проведенный в точку отрезкаВектор, соединяющий середины Вектор, проведенный в середину отрезка,Доказательстворавен полусумме векторов, проведенных из той же точки в его концы. ДоказательствоСABO Вектор, проведенный в точку отрезкаСABOmnДоказательствоТочка С делит отрезок АВ в отношении т : п. ДоказательствоСABOmn Вектор, соединяющий середины двух отрезков,СABDMNСABDMNДоказательстворавен полусумме векторов, соединяющих их концы. ДоказательствоСABDMN Вектор, проведенный в центроид треугольника,Центроид – точка пересечения медиан треугольника.СOABMДоказательстворавен одной трети ДоказательствоСOABMK Вектор, проведенный в точку пересечения диагоналей параллелограмма,ABCDOMДоказательстворавен одной четверти суммы векторов, проведенных ДоказательствоABCDOM Вектор, лежащий на диагонали параллелепипеда,CABDA1B1C1D1Доказательстворавен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины. ДоказательствоCABDA1B1C1D1 Помощь в управлении презентациейуправление презентацией осуществляется с помощью левой клавиши мышипереход Проверь себяУстные вопросыЗадача 1. Задача на доказательствоЗадача 2. Разложение векторовЗадача 3. Сложение Устные вопросыСправедливо ли утверждение:а) любые два противоположно направленных вектора коллинеарны?б) любые два Ответыа) ДАб) НЕТ (могут быть и противоположно направленными)в) ДАг) НЕТ (могут иметь разную длину)д) ДАе) ДА Задача 1. Задача на доказательствоBАCDA1B1C1D1M1M2Решение РешениеBАCDA1B1C1D1M1M2 Задача 2. Разложение векторовРазложите вектор по , и :а)б)в)г)РешениеABCDN Решениеа)б)в)г) Задача 3. 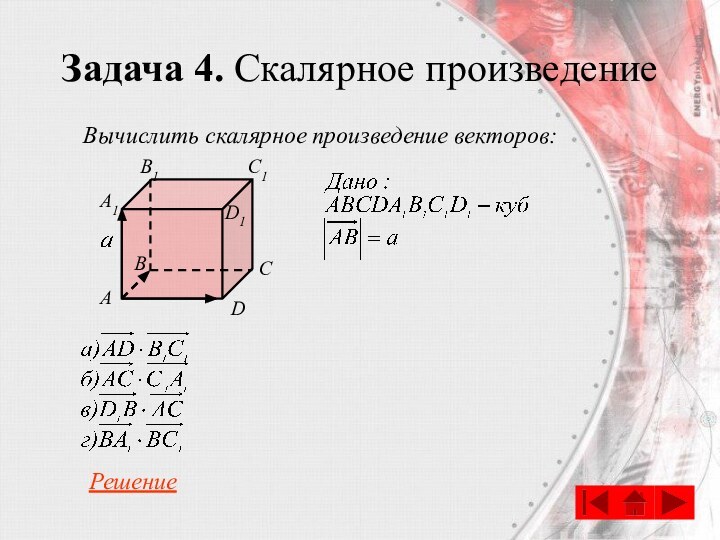Сложение и вычитаниеУпростите выражения:а)б)в)г)д)е)Решение Решениеа)б)в)г)д)е) Задача 4. Скалярное произведениеВычислить скалярное произведение векторов:CABDA1B1C1D1Решение Задача 4. Скалярное произведениеCABDA1B1C1D1O1Вычислить скалярное произведение векторов:Решение Решение Решение РешениеCABDA1B1C1D1O1 Об авторе Презентация выполнена ученицей 11 «Б» класса средней школы №316 Фрунзенского района
Слайды презентации

Слайд 2 Содержание
I. Понятие вектора в пространстве
II. Коллинеарные векторы
III. Компланарные векторы
IV. Действия с

Содержание I. Понятие вектора в пространствеII. Коллинеарные векторыIII. Компланарные векторыIV. Действия с векторамиV. Разложение вектораVI. Базисные задачиПроверь

векторами
V. Разложение вектора
VI. Базисные задачи

Проверь себя
Об авторе
Помощь в управлении презентацией

Выход

Слайд 3 Понятие вектора в пространстве
Вектор(направленный отрезок) –
отрезок, для

Понятие вектора в пространствеВектор(направленный отрезок) – отрезок, для которого указано какой

которого указано какой из его концов считается началом, а

какой – концом.



Длина вектора – длина отрезка AB.

А

В

M

Слайд 4 Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они

Коллинеарные векторыДва ненулевых вектора называются коллинеарными, если они лежат на одной

лежат на одной
прямой или параллельных прямых.

Среди коллинеарных различают:

Сонаправленные векторы
Противоположно направленные векторы

Слайд 5 Сонаправленные векторы
Сонаправленные векторы - векторы, лежащие
по одну

Сонаправленные векторыСонаправленные векторы - векторы, лежащие по одну сторону от прямой,

сторону от прямой, проходящей через их начала.
Нулевой вектор считается

сонаправленным с любым вектором.
Равные векторы

Слайд 6 Равные векторы
Равные векторы - сонаправленные векторы,
длины которых

Равные векторыРавные векторы - сонаправленные векторы, длины которых равны.От любой точки

равны.
От любой точки можно отложить вектор,
равный данному, и

притом только один.

Слайд 7 Противоположно направленные векторы
Противоположно направленные векторы – векторы, лежащие

Противоположно направленные векторыПротивоположно направленные векторы – векторы, лежащие по разные стороны

по разные стороны от прямой, проходящей через их начала.

Противоположные векторы

Слайд 8 Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины

Противоположные векторыПротивоположные векторы – противоположно направленные векторы, длины которых равны.Вектором, противоположным нулевому, считается нулевой вектор.

которых равны.





Вектором, противоположным нулевому,
считается нулевой вектор.

Слайд 9 Признак коллинеарности
Доказательство

Признак коллинеарностиДоказательство

Слайд 10 Доказательство признака коллинеарности

Доказательство признака коллинеарности

Слайд 11 Определение компланарных векторов
Компланарные векторы – векторы, при откладывании

Определение компланарных векторовКомпланарные векторы – векторы, при откладывании которых от одной

которых от одной и той же точки пространства, они

будут лежать в одной плоскости.
Пример:

B

А

C

D

A1

B1

C1

D1

Слайд 12 О компланарных векторах
Любые два вектора всегда компланарны.




Три вектора,

О компланарных векторахЛюбые два вектора всегда компланарны.Три вектора, среди которых имеются два коллинеарных, компланарны.αесли

среди которых имеются два коллинеарных, компланарны.

α
если

Слайд 13 Признак компланарности
Доказательство

Задачи

Признак компланарностиДоказательствоЗадачи

Слайд 14 Задачи на компланарность
Компланарны ли векторы:
а)
б)

Справка Решение
Известно, что векторы

Задачи на компланарностьКомпланарны ли векторы: а) б) Справка РешениеИзвестно, что векторы ,

, и компланарны.

Компланарны ли векторы:
а)
б)

Справка Решение

Слайд 15 Решение

Решение

Слайд 16 Решение

Решение

Слайд 17 Решение

Решение

Слайд 18 Доказательство признака компланарности
С
O
A1
B1
B
A

Доказательство признака компланарностиСOA1B1BA

Слайд 19 Свойство компланарных векторов

Свойство компланарных векторов

Слайд 20 Действия с векторами
Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

Действия с векторамиСложениеВычитаниеУмножение вектора на числоСкалярное произведение

Слайд 21 Сложение векторов

Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения

Сложение векторовПравило треугольникаПравило параллелограммаПравило многоугольникаПравило параллелепипедаСвойства сложения

Слайд 22 Правило треугольника
А
B
C

Правило треугольникаАBC

Слайд 23 Правило треугольника
А
B
C
Для любых трех точек А, В и

Правило треугольникаАBCДля любых трех точек А, В и С справедливо равенство:

С справедливо равенство:

Слайд 24 Правило параллелограмма
А
B
C

Правило параллелограммаАBC

Слайд 25 Свойства сложения

Свойства сложения

Слайд 26 Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого

Правило многоугольникаСумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при последовательном откладывании).BACDEПример

в конец последнего(при последовательном откладывании).
B
A
C
D
E
Пример

Слайд 27 Пример
C
A
B
D
A1
B1
C1
D1

ПримерCABDA1B1C1D1

Слайд 28 Правило параллелепипеда
B
А
C
D
A1
B1
C1
D1
Вектор, лежащий на диагонали параллелепипеда, равен сумме

Правило параллелепипедаBАCDA1B1C1D1Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из

векторов, проведенных из той же точки и лежащих на

трех измерениях параллелепипеда.

Слайд 29 Свойства
B
А
C
D
A1
B1
C1
D1

СвойстваBАCDA1B1C1D1

Слайд 30 Вычитание векторов
Вычитание
Сложение с противоположным

Вычитание векторовВычитаниеСложение с противоположным

Слайд 31 Вычитание
Разностью векторов и называется

ВычитаниеРазностью векторов и называется такойвектор, сумма которого с вектором равнавектору .

такой
вектор, сумма которого с вектором равна
вектору

.

Слайд 32 Вычитание
B
A
Правило трех точек
C

ВычитаниеBAПравило трех точек C

Слайд 33 Правило трех точек
Любой вектор можно представить как разность

Правило трех точекЛюбой вектор можно представить как разность двух векторов, проведенных из одной точки.АBK

двух векторов, проведенных из одной точки.
А
B
K

Слайд 34 Сложение с противоположным
Разность векторов и

Сложение с противоположнымРазность векторов и можно представить как сумму

можно представить как сумму вектора

и вектора, противоположного вектору .

А

B

O

Слайд 35 Умножение вектора на число

Умножение вектора на число

Слайд 36 Свойства
Произведением нулевого вектора на любое число считается нулевой

СвойстваПроизведением нулевого вектора на любое число считается нулевой вектор.Произведение любого вектора

вектор.

Произведение любого вектора на число нуль есть нулевой вектор.

Слайд 37 Свойства

Свойства

Слайд 38 Скалярное произведение
Скалярным произведением двух векторов называется произведение их

Скалярное произведениеСкалярным произведением двух векторов называется произведение их длин на косинус

длин на косинус угла между ними.
Справедливые утверждения
Вычисление скалярного произведения

в координатах
Свойства скалярного произведения

Слайд 39 Справедливые утверждения
скалярное произведение ненулевых векторов
равно нулю

Справедливые утверждения скалярное произведение ненулевых векторов равно нулю тогда и только

тогда и только тогда, когда эти векторы перпендикулярны

скалярный

квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату
его длины

Слайд 40 Вычисление скалярного произведения в координатах
Доказательство

Вычисление скалярного произведения в координатахДоказательство

Слайд 41 Доказательство формулы скалярного произведения
O
A
B
α
O
B
A
O
B
A

Доказательство формулы скалярного произведенияOABαOBAOBA

Слайд 42 Доказательство формулы скалярного произведения

Доказательство формулы скалярного произведения

Слайд 43 Свойства скалярного произведения


10.
20.
30.
40.
(переместительный закон)
(распределительный закон)
(сочетательный закон)

Свойства скалярного произведения10.20.30.40.(переместительный закон)(распределительный закон)(сочетательный закон)

Слайд 44 Разложение вектора
По двум неколлинеарным векторам
По трем некомпланарным векторам

Разложение вектораПо двум неколлинеарным векторамПо трем некомпланарным векторам

Слайд 45 Разложение вектора по двум неколлинеарным векторам
Теорема.
Любой вектор

Разложение вектора по двум неколлинеарным векторамТеорема. Любой вектор можно разложить по

можно разложить по двум
данным неколлинеарным векторам, причем коэффициенты

разложения определяются единственным образом.

Доказательство

Слайд 46 Доказательство теоремы
O
A
A1
B
P

Пусть коллинеарен

Доказательство теоремыOAA1BPПусть коллинеарен .Тогда ,

.
Тогда

, где y – некоторое число. Следовательно,

т.е. разложен по векторам и .

Слайд 47 не коллинеарен ни вектору

не коллинеарен ни вектору , ни вектору .Отметим

, ни вектору .
Отметим О – произвольную

точку.


Доказательство теоремы

Слайд 48 Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом.
Допустим:
Тогда:

-

Доказательство теоремыДокажем, что коэффициенты разложения определяются единственным образом.Допустим:Тогда:-

Слайд 49 Разложение вектора по трем некомпланарным векторам
Если вектор p

Разложение вектора по трем некомпланарным векторамЕсли вектор p представлен в видегде

представлен в виде

где x, y, z – некоторые числа,

то говорят, что вектор
разложен по векторам , и .
Числа x, y, z называются коэффициентами разложения.

Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Доказательство

Слайд 50 Доказательство теоремы
С
O
A
B
P1
P2
P

Доказательство теоремыСOABP1P2P

Слайд 51 Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом.
Допустим:
Тогда:
-

Доказательство теоремыДокажем, что коэффициенты разложения определяются единственным образом.Допустим:Тогда:-

Слайд 52 Базисные задачи
Вектор, проведенный в середину отрезка
Вектор, проведенный в

Базисные задачиВектор, проведенный в середину отрезкаВектор, проведенный в точку отрезкаВектор, соединяющий

точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид

треугольника

Вектор, проведенный в точку пересечения
диагоналей параллелограмма

Вектор, лежащий на диагонали параллелепипеда

Слайд 53 Вектор, проведенный в середину отрезка,
Доказательство
равен полусумме векторов, проведенных

Вектор, проведенный в середину отрезка,Доказательстворавен полусумме векторов, проведенных из той же точки в его концы.

из той же точки в его концы.

Слайд 54 Доказательство
С
A
B
O

ДоказательствоСABO

Слайд 55 Вектор, проведенный в точку отрезка
С
A
B
O
m
n
Доказательство
Точка С делит отрезок

Вектор, проведенный в точку отрезкаСABOmnДоказательствоТочка С делит отрезок АВ в отношении т : п.

АВ в отношении т : п.

Слайд 56 Доказательство
С
A
B
O
m
n

ДоказательствоСABOmn

Слайд 57 Вектор, соединяющий середины двух отрезков,
С
A
B
D
M
N
С
A
B
D
M
N
Доказательство
равен полусумме векторов, соединяющих

Вектор, соединяющий середины двух отрезков,СABDMNСABDMNДоказательстворавен полусумме векторов, соединяющих их концы.

их концы.

Слайд 58 Доказательство
С
A
B
D
M
N

ДоказательствоСABDMN

Слайд 59 Вектор, проведенный в центроид треугольника,
Центроид – точка пересечения

Вектор, проведенный в центроид треугольника,Центроид – точка пересечения медиан треугольника.СOABMДоказательстворавен одной

медиан треугольника.
С
O
A
B
M
Доказательство
равен одной трети суммы векторов, проведенных из этой

точки в вершины треугольника.

Слайд 60 Доказательство
С
O
A
B
M
K

ДоказательствоСOABMK

Слайд 61 Вектор, проведенный в точку пересечения диагоналей параллелограмма,
A
B
C
D
O
M
Доказательство
равен одной

Вектор, проведенный в точку пересечения диагоналей параллелограмма,ABCDOMДоказательстворавен одной четверти суммы векторов,

четверти суммы векторов, проведенных из этой точки в вершины

параллелограмма.

Слайд 62 Доказательство
A
B
C
D
O
M

ДоказательствоABCDOM

Слайд 63 Вектор, лежащий на диагонали параллелепипеда,
C
A
B
D
A1
B1
C1
D1
Доказательство
равен сумме векторов, лежащих

Вектор, лежащий на диагонали параллелепипеда,CABDA1B1C1D1Доказательстворавен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.

на трех его ребрах, исходящих из одной вершины.

Слайд 64 Доказательство
C
A
B
D
A1
B1
C1
D1

ДоказательствоCABDA1B1C1D1

Слайд 65 Помощь в управлении презентацией
управление презентацией осуществляется с помощью

Помощь в управлении презентациейуправление презентацией осуществляется с помощью левой клавиши мышипереход

левой клавиши мыши
переход от одного слайда к другому и

на гиперссылки по одиночному щелчку
завершение презентации при нажатии кнопки выход
переход к следующему слайду
возврат к содержанию
возврат к подтеме
возврат с гиперссылок

Слайд 66 Проверь себя
Устные вопросы
Задача 1. Задача на доказательство
Задача 2.

Проверь себяУстные вопросыЗадача 1. Задача на доказательствоЗадача 2. Разложение векторовЗадача 3.

Разложение векторов
Задача 3. Сложение и вычитание векторов
Задача 4. Скалярное

произведение

Слайд 67 Устные вопросы
Справедливо ли утверждение:
а) любые два противоположно направленных

Устные вопросыСправедливо ли утверждение:а) любые два противоположно направленных вектора коллинеарны?б) любые

вектора коллинеарны?
б) любые два коллинеарных вектора сонаправлены?
в) любые два

равных вектора коллинеарны?
г) любые два сонаправленных вектора равны?
д)
е) существуют векторы , и такие, что
и не коллинеарны, и не коллинеарны, а
и коллинеарны?

Ответы

Слайд 68 Ответы
а) ДА
б) НЕТ (могут быть и противоположно направленными)
в)

Ответыа) ДАб) НЕТ (могут быть и противоположно направленными)в) ДАг) НЕТ (могут иметь разную длину)д) ДАе) ДА

ДА
г) НЕТ (могут иметь разную длину)
д) ДА
е) ДА

Слайд 69 Задача 1. Задача на доказательство
B
А
C
D
A1
B1
C1
D1
M1
M2
Решение

Задача 1. Задача на доказательствоBАCDA1B1C1D1M1M2Решение

Слайд 70 Решение
B
А
C
D
A1
B1
C1
D1
M1
M2

РешениеBАCDA1B1C1D1M1M2

Слайд 71 Задача 2. Разложение векторов
Разложите вектор по

Задача 2. Разложение векторовРазложите вектор по , и :а)б)в)г)РешениеABCDN

, и :






а)
б)
в)
г)
Решение
A
B
C
D
N

Слайд 72 Решение
а)
б)
в)
г)

Решениеа)б)в)г)

Слайд 73 Задача 3. Сложение и вычитание
Упростите выражения:
а)
б)
в)
г)
д)
е)

Решение

Задача 3. Сложение и вычитаниеУпростите выражения:а)б)в)г)д)е)Решение

Слайд 74 Решение
а)
б)
в)
г)
д)


е)

Решениеа)б)в)г)д)е)

Слайд 75 Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов:
C
A
B
D
A1
B1
C1
D1
Решение

Задача 4. Скалярное произведениеВычислить скалярное произведение векторов:CABDA1B1C1D1Решение

Слайд 76 Задача 4. Скалярное произведение
C
A
B
D
A1
B1
C1
D1
O1
Вычислить скалярное произведение векторов:
Решение

Задача 4. Скалярное произведениеCABDA1B1C1D1O1Вычислить скалярное произведение векторов:Решение

Слайд 77 Решение

Решение

Слайд 78 Решение

Решение

Слайд 79 Решение
C
A
B
D
A1
B1
C1
D1
O1

РешениеCABDA1B1C1D1O1
  • Имя файла: opredelenie-vektora-v-prostranstve.pptx
  • Количество просмотров: 123
  • Количество скачиваний: 0
- Предыдущая Электрический ток в газах
Следующая - Танцевальный коллектив Родничок

Похожие презентации

Сложение однозначных чисел с переходом через десяток, вида +7 Сложение однозначных чисел с переходом через десяток, вида +7 90
Презентация у року Единицы измерения длины. Километр Презентация у року Единицы измерения длины. Километр 149
Презентация по математике на тему : Решение задач Презентация по математике на тему : Решение задач 110
Признак перпендикулярности плоскостей Признак перпендикулярности плоскостей 165
Перестановочные тесты и бутстреп анализ Перестановочные тесты и бутстреп анализ 138
Презентация по математике Мат диктант Окружность Презентация по математике Мат диктант Окружность 97
Координатная плоскость 6 класс Координатная плоскость 6 класс 164
Открытый урок по математике по системе Занкова Вычитание трехзначных чисел с переходом через разряд 3 класс план-конспект урока (математика, 3 класс) Открытый урок по математике по системе Занкова Вычитание трехзначных чисел с переходом через разряд 3 класс план-конспект урока (математика, 3 класс) 48
Методы решения тригонометрических уравнений Методы решения тригонометрических уравнений 89
Внеурочное занятие по математике 2 класс Старинные меры длины план-конспект занятия по математике (2 класс) Внеурочное занятие по математике 2 класс Старинные меры длины план-конспект занятия по математике (2 класс) 140
Случайные события Случайные события 127
все о призме все о призме 91
Презентация .Календарь презентация к уроку по математике (3 класс) по теме Презентация .Календарь презентация к уроку по математике (3 класс) по теме 161
Открытый урок по математике в 1 классе 2-ая четверть Закрепление изученного план-конспект урока по математике (1 класс) по теме Открытый урок по математике в 1 классе 2-ая четверть Закрепление изученного план-конспект урока по математике (1 класс) по теме 153
Презентация к внеклассному мероприятию Своя игра Презентация к внеклассному мероприятию Своя игра 103
Измерение площади с помощью палетки презентация к уроку по математике (4 класс) Измерение площади с помощью палетки презентация к уроку по математике (4 класс) 182
Решение уравнений Решение уравнений 123
Презентация по математике на тему Действия с десятичными дробями Презентация по математике на тему Действия с десятичными дробями 107
Математический бой Математический бой 138
Треугольник Треугольник 130
Вычисление площадей плоских фигур с помощью определенного интеграла Вычисление площадей плоских фигур с помощью определенного интеграла 109
Презентация к уроку по теме Вычитание по одному Презентация к уроку по теме Вычитание по одному 111
Четырехугольники Четырехугольники 114
Викторина по геометрии Викторина по геометрии 121
Скорость сближения Скорость сближения 124
didakticheskaya igra didakticheskaya igra 112
Игра - тренажер Угадай -ка тренажёр по математике (подготовительная группа) Игра - тренажер Угадай -ка тренажёр по математике (подготовительная группа) 116
Пересекающиеся линии. презентация к уроку математики (1 класс) по теме Пересекающиеся линии. презентация к уроку математики (1 класс) по теме 114
Параллелепипед Параллелепипед 88
Путешествие в страну Тик-Так учебно-методическое пособие по математике (подготовительная группа) Путешествие в страну Тик-Так учебно-методическое пособие по математике (подготовительная группа) 119