Слайд 2
СОБЫТИЯ И ИСПЫТАНИЯ
Предметом исследования в теории вероятностей являются
события, появляющиеся при определенных условиях, которые можно воспроизводить неограниченное
количество раз.
Каждое осуществление этих условий называют испытанием
Слайд 3
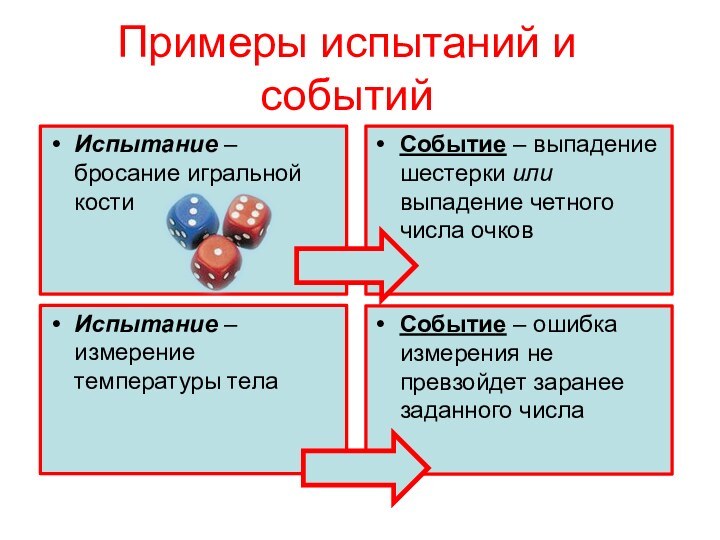
Примеры испытаний и событий
Испытание – бросание игральной кости
Событие
– выпадение шестерки или выпадение четного числа очков
Испытание –
измерение температуры тела
Событие – ошибка измерения не превзойдет заранее заданного числа
Слайд 4
Случайные события
Событие называется случайным, если при
одних и тех же условиях оно может как произойти,
так и не произойти.
Слайд 5
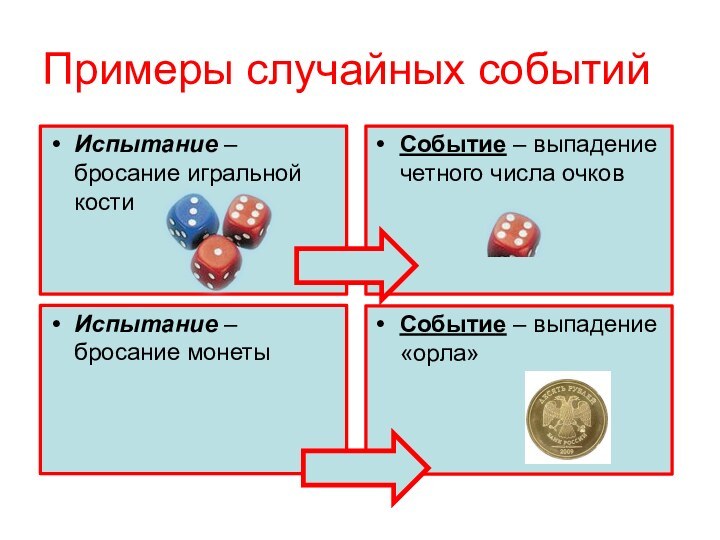
Примеры случайных событий
Испытание – бросание игральной кости
Событие –
выпадение четного числа очков
Испытание – бросание монеты
Событие – выпадение
«орла»
Слайд 6
Вероятность случайного события
Степень объективной возможности случайного события можно
измерять числом.
Это число называется
вероятностью случайного события.
Около этого
числа группируются относительные частоты данного случайного события
Слайд 7
Абсолютная и относительная частота
Слайд 8
Статистическое определение вероятности
Вероятностью события А в данном испытании
называют число P(A), около которого группируются значения относительной частоты
при большом числе испытаний n.
Слайд 9
Совместимые и несовместимые события
События A и B
называются совместимыми, если появление одного из них не исключает
появления другого.
События A и B называются несовместимыми, если появление одного из них исключает появление другого (не могут наступить одновременно).
Слайд 10
Примеры совместимых и несовместимых событий
Испытание – бросание двух
игральных кубиков
События:
А - выпадение четной суммы очков и
В - выпадение равных чисел на обоих кубиках;
Испытание – однократно бросание монеты
События –
А - выпадение «орла»
и В - выпадение «решки»
совместимые
несовместимые
Слайд 11
Противоположные события
С каждым событием A связано
противоположное событие В, состоящее в том, что событие A
не осуществляется.
Противоположные события, очевидно, несовместимы.
Сумма вероятностей противоположных событий равна 1
Слайд 12
Примеры противоположных событий
На кубике выпадет четное число и
на кубике выпадет нечетное число;
Монета упала орлом вверх и
монета упала вверх решкой;
Лампа горит и лампа не горит.
Слайд 13
Полной группой событий называется множество всех событий для
данного испытания, если его результатом становится выполнение хотя бы
одного из них .
Слайд 14
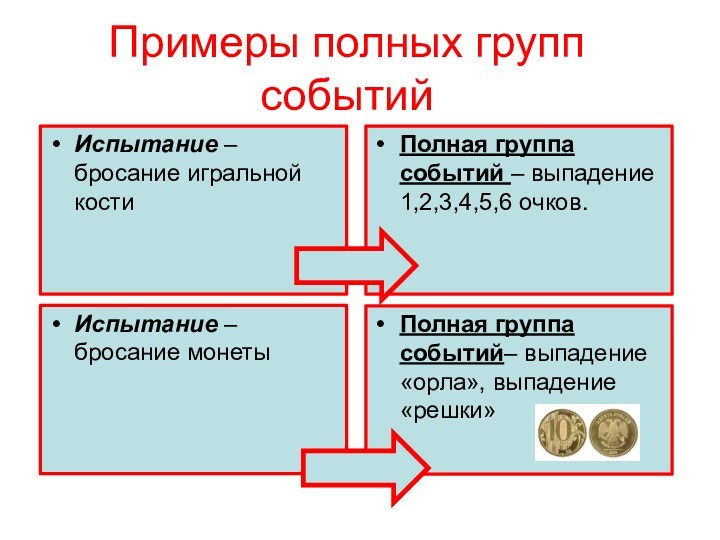
Примеры полных групп событий
Испытание – бросание игральной кости
Полная
группа событий – выпадение 1,2,3,4,5,6 очков.
Испытание – бросание монеты
Полная
группа событий– выпадение «орла», выпадение «решки»
Слайд 17
Классическое определение вероятности
Слайд 18
Достоверные события
Событие называется достоверным, если оно наступает
всегда, при любом испытании.
Вероятность достоверного события
всегда равна 1.
Слайд 19
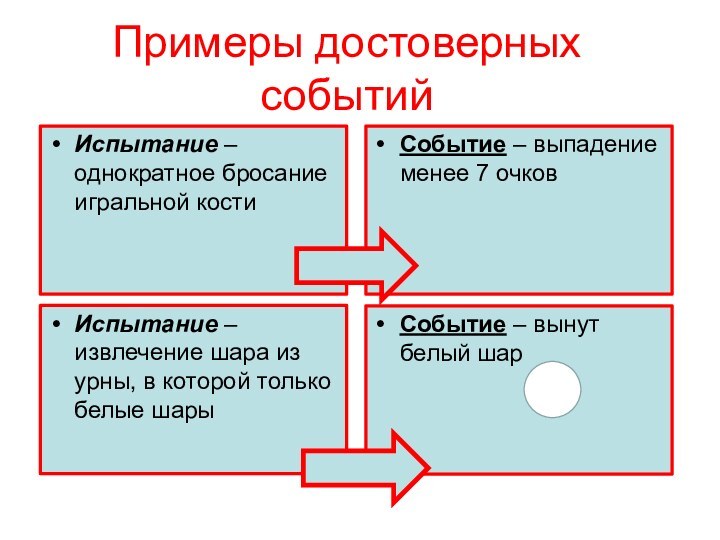
Примеры достоверных событий
Испытание – однократное бросание игральной кости
Событие
– выпадение менее 7 очков
Испытание – извлечение шара из
урны, в которой только белые шары
Событие – вынут белый шар
Слайд 20
Невозможные события
Событие называют невозможным, если оно
не наступает никогда, то есть благоприятных исходов для него
0.
Вероятность невозможного события равна 0 .
Слайд 21
Примеры невозможных событий
Испытание – бросание игральной кости
Событие –
выпадение семи очков
Испытание – извлечение шара из урны, в
которой только белые шары
Событие – вынут черный шар
Слайд 22
Независимые события
Несколько событий А1, А2,…Аk называются независимыми в
совокупности, если вероятность появления любого из них не зависит
от того, произошли какие-либо другие рассматриваемые события или нет.
В противном случае события называют зависимыми.
Слайд 23
Примеры независимых событий
На обоих кубиках выпадет шестерка;
При подбрасывании
двух монет выпадут два орла;
При вытаскивании двух шаров из
урны оба шара будут красными.
Слайд 24
Сумма событий
Суммой событий А и В называют событие
С=А+В, состоящее в наступлении хотя бы одного из событий
А или В
Слайд 25
Пример суммы событий
Испытание – стрельба двух стрелков (каждый
делает по одному выстрелу)
А – попадание в мишень 1
стрелка;
В – попадание в мишень 2 стрелка;
С=А+В – попадание в мишень хотя бы одним стрелком.
Слайд 26
Произведение событий
Произведением событий А и В называют событие
С=АВ, состоящее в том, что в результате испытания произошло
и событие А и событие В.
Слайд 27
Пример произведения событий
Испытание – стрельба двух стрелков (каждый
делает по одному выстрелу)
А – попадание в мишень 1
стрелка;
В – попадание в мишень 2 стрелка;
С=АВ – оба стрелка попали в мишень.
Слайд 28
Теорема сложения вероятностей несовместимых событий
Вероятность суммы двух несовместимых
событий равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Слайд 29
Теорема умножения вероятностей независимых событий
Вероятность произведения двух независимых
равна произведению вероятностей этих событий
Р(АВ)=Р(А)Р(В)
Слайд 30
Теорема сложения вероятностей совместимых событий
Вероятность суммы двух совместимых
событий А и В равна сумме вероятностей этих событий
минус вероятность их произведения:
Р(А+В)=Р(А)+Р(В)-Р(АВ)
Слайд 31
В случайном эксперименте симметричную монету бросают четырежды. Найдите
вероятность того, что орел не выпадет ни разу.
Условие можно
трактовать так: какова вероятность того,
что все четыре раза выпадет решка?
К-во благоприятных
событий m=?
К-во всех событий группы n=?
m=1
Четыре раза выпала
решка.
1-й раз - 2 варианта
2-й раз - 2 варианта
3-й раз - 2 варианта
4-й раз - 2 варианта
Слайд 32
В урне 3 белых и 9 черных шаров.
Из урны наугад вынимается 1 шар. Какова вероятность того,
что вынутый шар окажется белым?
Решение:
Количество всех возможных результатов n=3+9=12.
Опытов, в результате которых может быть вынут белый шар m=3.
Ответ: 0, 25
Слайд 33
Случайной величиной называется переменная величина, которая в результате
испытания может принять одно значение из множества возможных.
Если
значения величины можно записать в виде конечной или бесконечной последовательности, то такая величина называется дискретной.
Слайд 34
Пример 1. В студенческой группе 25 человек. Пусть
величина Х – число студентов, находящихся в аудитории перед
началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.
При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.
Слайд 35
Закон распределения случайной величины
Соответствие между всеми возможными значениями
дискретной случайной величины и их вероятностями называется законом распределения
данной случайной величины.
Слайд 36
Простейшая формой задания закона распределения дискретной случайной величины
является таблица, в которой перечислены возможные значения случайной величины
(обычно в порядке возрастания) и соответствующие им вероятности. Такая таблица называется рядом распределения.
.
Слайд 37
Допустим, что число возможных значений случайной величины конечно:
х1, х2, …, хn.
При одном испытании случайная величина
принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, … , n) образуют полную группу попарно независимых событий.
Следовательно сумма вероятностей всех событий,
р1 + р2 + … + рn = 1.
Слайд 38
Математическое ожидание
случайной величины Х указывает некоторое среднее значение,
около которого группируются все возможные значения Х.
Слайд 39
Математическое ожидание дискретной случайной величины
Слайд 43
Среднее квадратичное отклонение
Слайд 44
Генеральная совокупность и выборка
Пусть требуется изучить множество однородных
объектов. Назовем это множество статистической совокупностью.
Статистическая совокупность, из
которой отбирается часть объектов называется генеральной совокупностью.
Множество объектов, случайным образом отобранных из генеральной совокупности называют выборкой.
Слайд 45
Объем генеральной совокупности и выборки
Это соответственно число элементов
генеральной совокупности и выборки.
Если элементы в выборке не повторяются,
то выборка называется бесповторной, иначе – выборкой с повторениями
Слайд 46
Репрезентативная выборка
Свойства объектов выборки должны правильно отражать свойства
объектов генеральной совокупности, тогда выборка считается репрезентативной.
Считается, что выборка
репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.
Слайд 49
Статистическим распределением выборки
называется перечень вариант и соответствующих им
частот (или относительных частот).
Для графического изображения статистического распределения
используются
полигоны и гистограммы.
Слайд 50
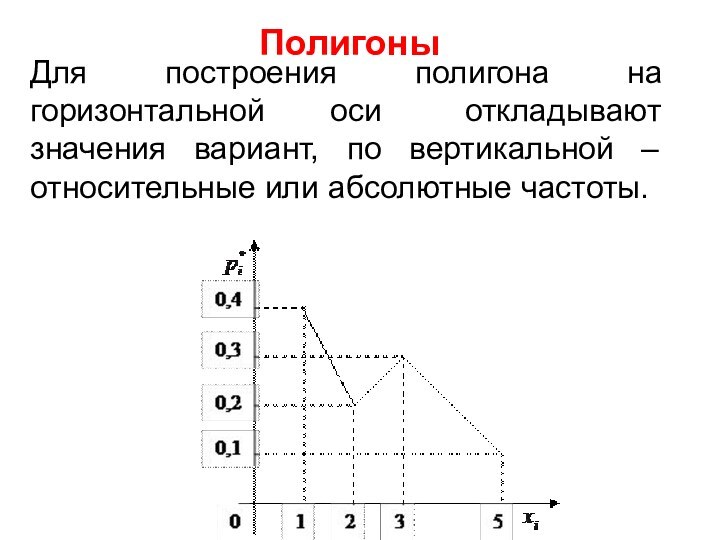
Полигоны
Для построения полигона на горизонтальной оси откладывают значения
вариант, по вертикальной – относительные или абсолютные частоты.
Слайд 51
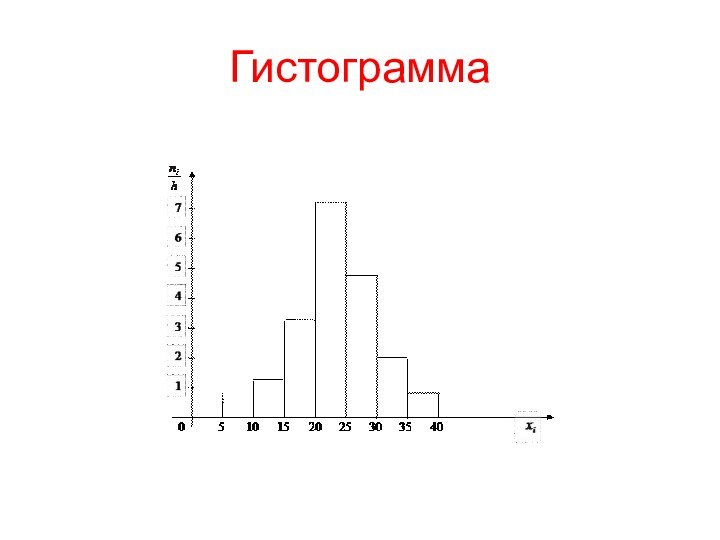
Гистограммы
В случае большого числа вариант и в случае
непрерывного распределения признака, строят гистограммы, разбивая вариационный ряд на
интервалы.
Слайд 52
Построение гистограмм
Сначала вариационный ряд разбивается на несколько интервалов
(чаще одинаковых).
Интервалы откладываются на горизонтальной оси
Затем над каждым
из рисуется прямоугольник. Если все интервалы были одинаковыми, то высота каждого прямоугольника пропорциональна числу элементов выборки, попадающих в соответствующий интервал. Если интервалы разные, то высота прямоугольника выбирается таким образом, чтобы его площадь была пропорциональна числу элементов выборки, которые попали в этот интервал.
Слайд 54
Генеральная и выборочная средняя
.
Слайд 55
Генеральная и выборочная дисперсия
Слайд 56
Мода и медиана
Модой выборки называется вариант, которому соответствует
наибольшая частота.
Медианой выборки называется значение признака, приходящееся на середину
ранжированного ряда наблюдений.
Слайд 57
Для определения медианы в дискретном ряду при наличии частот: 1)
сначала вычисляют полусумму частот n/2, то есть находят номер
серединного элемента вариационного ряда.
2) затем определяют, какое значение варианта приходится на этот элемент ряда.
Слайд 58
Например, если всего в выборке было n=60 элементов,
то медианой будет то значение признака, которое приходится на
n/2=30, то есть на 30-й элемент ряда.
Слайд 59
Функцией распределения случайной величины Х
называют функцию F(x), определяющую для каждого
значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.
F(x)
= p (X
Слайд 60
Функция распределения дискретной случайной величины
Слайд 61
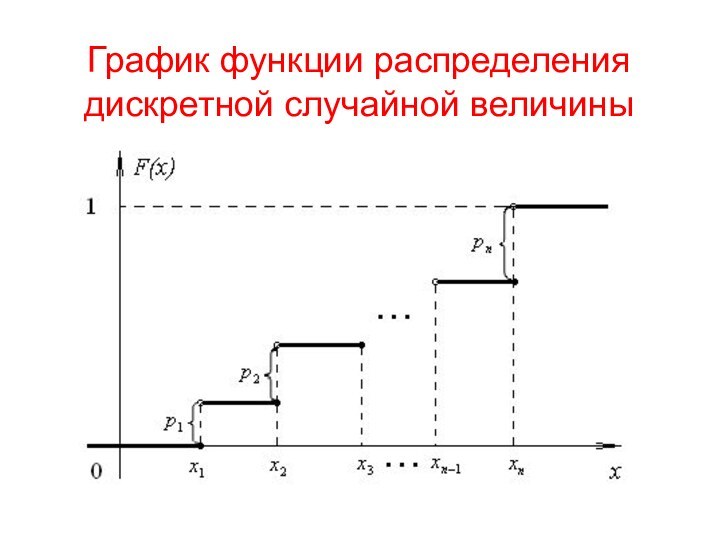
График функции распределения дискретной случайной величины
Слайд 63
Несмещённая оценка
в математической статистике — это точечная оценка, математическое ожидание которой равно оцениваемому
параметру.
Выборочная средняя является несмещенной оценкой математического ожидания.