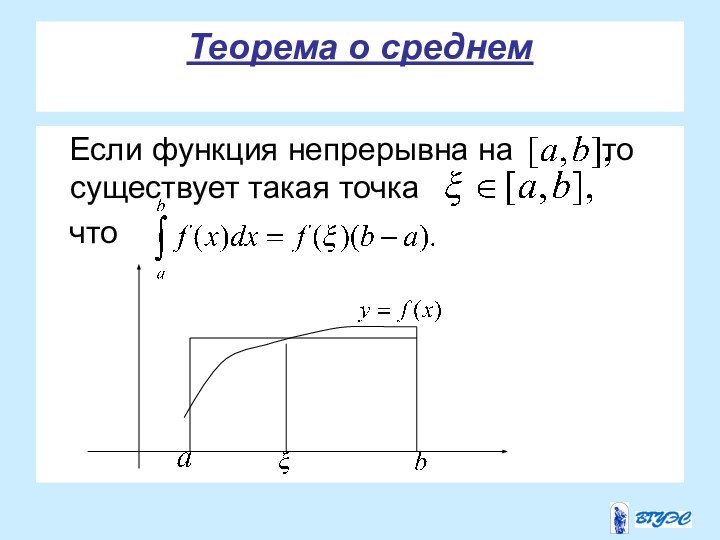
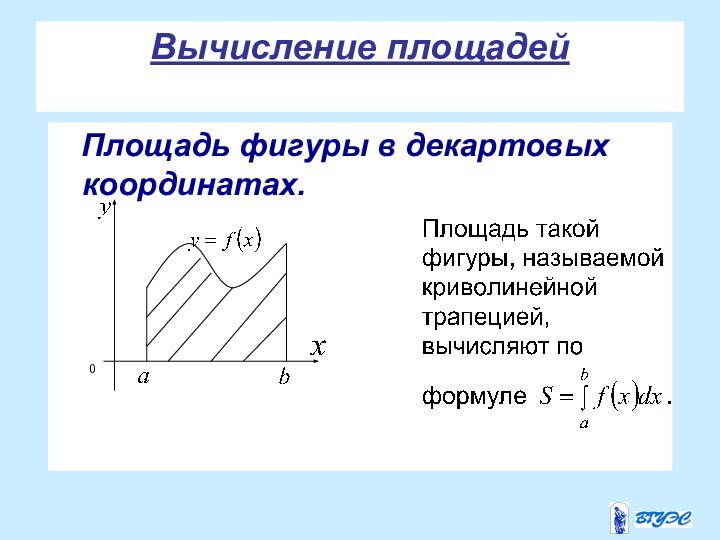
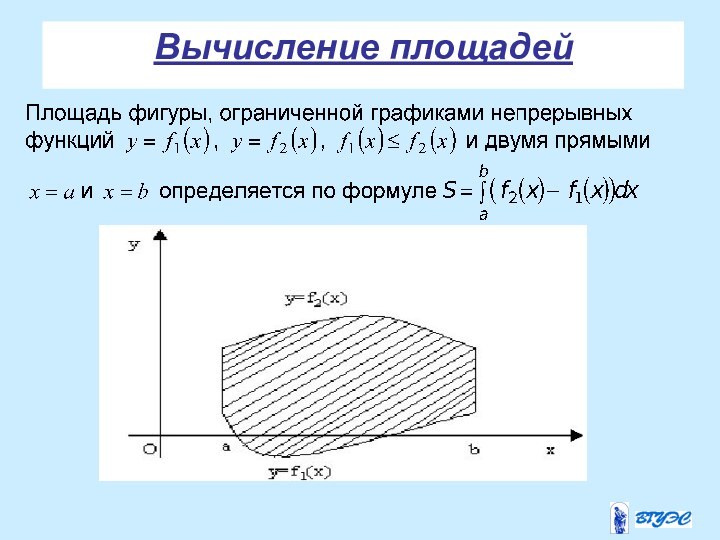
задачу о вычислении площади фигуры, ограниченной графиком функции
, отрезками прямых, и осью Ox.Такую фигуру называют криволинейной трапецией
a
b
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





















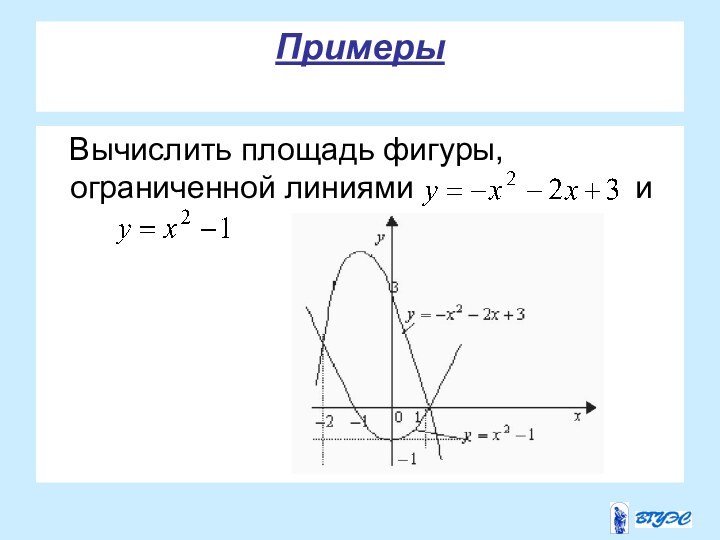











a
b
.