Презентация на тему Определенный интеграл

P.
Вопрос: что такое площадь криволинейной трапеции? Что такое площадь

многоугольника мы знаем.
Схема «Т»
Разобьём [a,b] точками
a = x0 < x1 < x2 < … < xn-1 < xn = b
на конечное число частей. Точки берем произвольно. Таким образом, получаем разбиение
T = {[x0,x1], [x1,x2], …, [xn-1,xn]}
отрезка [a,b] на более мелкие отрезки.

а полученные отрезки – отрезками разбиения.
2. Обозначим через
x1 =

x1 – x0, x2 = x2 – x1, …, xn = xn – xn-1,
где xi – длина i-того отрезка (i =1, 2, …, n).
Введем по определению:
(T) = max xi
1  i  n
Назовем (T) рангом разбиения T. Это наибольшая из длинн отрезков разбиения.
3. Выберем в каждом из отрезков разбиения произвольно по точке:

 [xn-1,xn]










Вычисляем значения функции в этой точке:
f (1), f

(2), …, f (n).

f (2)x2 + … + f (n)xn =



S(T )

называется интегральной суммой функции f по данному разбиению T.
Таким образом, геометрически S(T ) – площадь ступенчатой фигуры (сумма площадей прямоугольников).
S(T ) – это число.
Разбивая по другому отрезок [a,b] на части и выбирая по другому точки i всякий раз будем

образом, можно говорить о переменной интегральной суммы на данном

отрезке. Но эта переменная величина более сложной природы, нежели те, что были до сих пор. Введем понятие предела этой переменной величины.
Определение 2. Число I называется пределом переменной интегральной суммы S(T ) функции f (x) на отрезке [a,b] при (T)  0 если:
  R+    R+  T ((T) <   S(T ) – I< )

Обозначают:

выбора точек i.
Конец схемы «Т»
Замечание 1. Высказывание в определении

2 означает, что когда (T)  0  S(T )  I.
Замечание 2. Если (T)  0, то очевидно, что число отрезков разбиения n стремится к бесконечности.
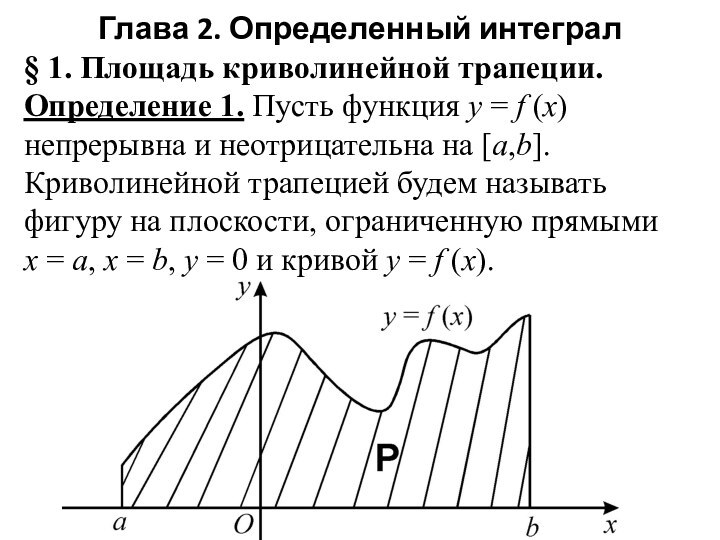
Определение 3. Пусть функция y = f (x) непрерывна и неотрицательна на отрезке [a,b] и P – ее криволинейная трапеция. Если существу-ет конечный предел

нами предел переменной интегральной суммы обладает всеми обычными свойствами

предела.

§ 2. Понятие определенного интеграла. Условие его существования.
Пусть y = f (x) произвольная функция на отрезке [a,b]. Применим к этой функции схему «Т» (разбиение Т, (T), i, f (i), S(T ), ).

переменной интегральной суммы, не зависящий от вида разбиения и

выбора точек i, то этот предел называется определенным интегралом (или интегралом Римана) функции f на отрезке [a,b].

Обозначается:

Таким образом:

где: f (x) – подынтегральная функция,
f (x)dx – подынтегральное выражение,

интегрирования,
[a,b] – отрезок интегрирования.
Функция f (x) называется интегрируемой по

Риману на данном отрезке.
Геометрический смысл определенного интеграла.
Возвращаясь к задаче о площади криволинейной трапеции, можем утверждать, что для неотрицательной и непрерывной функции

y = f (x) на отрезке [a,b], численно равен

площади соответствующей криволинейной трапеции