- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определенный интеграл
Содержание
- 2. Элементы интегрального исчисления1.Определение определенного интеграла 2.Основные свойства определенного интеграла3.Формула Ньютона-Лейбница4.Методы интегрирования5.Геометрические приложения определенного интеграла6.Несобственные интегралы.
- 3. Определенный интеграл, его свойства и вычисление
- 4. Понятие определенного интегралаРассмотрим функцию y=f(x), непрерывную и
- 5. Геометрическое изображение определения
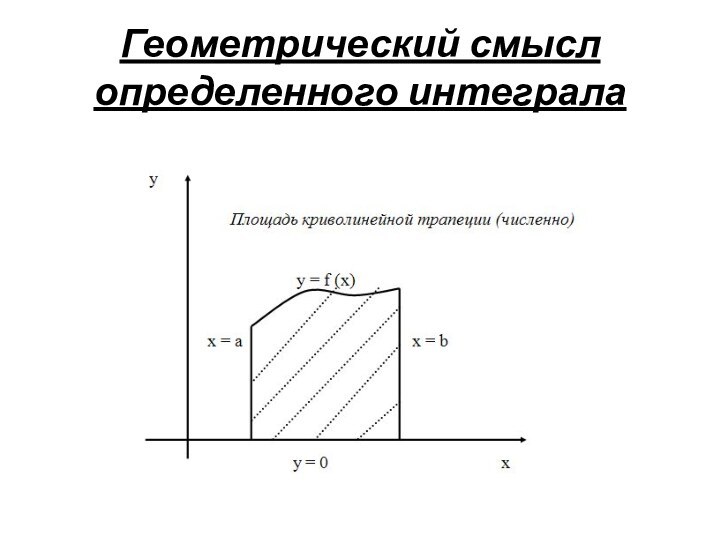
- 6. Определение интегральной суммыИнтегральной суммой для функции y=f(x)
- 7. Определение определенного интегралаОпределенным интегралом от функции f(x)
- 8. Геометрический смысл определенного интеграла
- 9. Основные свойства определенного интеграла10 Величина определенного интеграла
- 10. Основные свойства определенного интеграла30 Если промежуток интегрирования
- 11. Основные свойства определенного интеграла40 Определенный интеграл от
- 12. Основные свойства определенного интеграла50. Если подынтегральная функция
- 13. Основные свойства определенного интеграла70. Определенный интеграл от
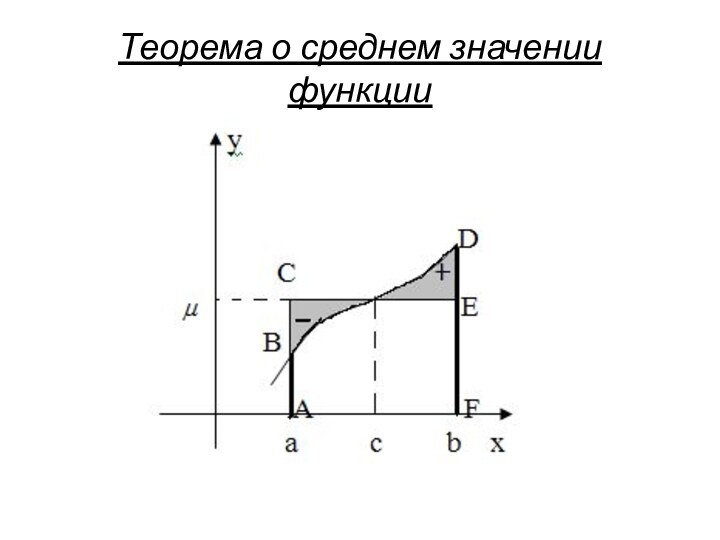
- 14. Теорема о среднем значении функции
- 15. Формула Ньютона-Лейбница.Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования.
- 16. Методы интегрирования
- 17. Непосредственное интегрированиеЭтот способ основан на использовании свойств
- 18. Замена переменнойВычислить.
- 19. Интегрирование по частямВычислить.
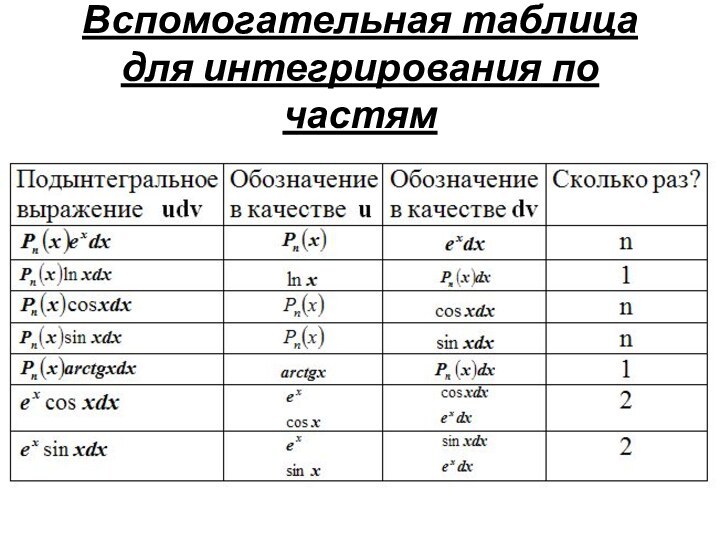
- 20. Вспомогательная таблица для интегрирования по частям
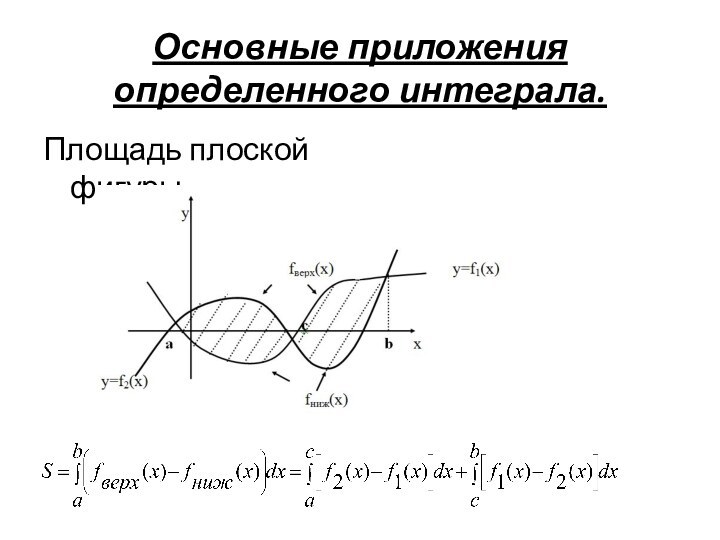
- 21. Скачать презентацию
- 22. Похожие презентации
Элементы интегрального исчисления1.Определение определенного интеграла 2.Основные свойства определенного интеграла3.Формула Ньютона-Лейбница4.Методы интегрирования5.Геометрические приложения определенного интеграла6.Несобственные интегралы.



![Определенный интеграл Понятие определенного интегралаРассмотрим функцию y=f(x), непрерывную и ограниченную на отрезке [a,b]. Разобьем](/img/tmb/15/1444315/0654f04372ac17f99235a884a9ffddf0-720x.jpg)

![Определенный интеграл Определение интегральной суммыИнтегральной суммой для функции y=f(x) на отрезке [a,b] называется сумма](/img/tmb/15/1444315/0d22014f335e4150b677a67ea5313912-720x.jpg)
![Определенный интеграл Определение определенного интегралаОпределенным интегралом от функции f(x) на отрезке [a,b] называется предел](/img/tmb/15/1444315/4b5cbcfcc74688d9c0a991ee0a2d00a5-720x.jpg)

![Определенный интеграл Основные свойства определенного интеграла30 Если промежуток интегрирования [a,b] разбит на конечное число](/img/tmb/15/1444315/9ff933d795259af668c791c3055d73b3-720x.jpg)








Слайд 2
Элементы интегрального исчисления
1.Определение определенного интеграла
2.Основные свойства определенного
интеграла
Слайд 4
Понятие определенного интеграла
Рассмотрим функцию y=f(x), непрерывную и ограниченную
на отрезке [a,b]. Разобьем [a,b] на n элементарных отрезков
∆xi произвольной длины, возьмем на каждом отрезке ∆xi произвольную точку ci и вычислим значение функции f(ci) в этих точках.
Слайд 6
Определение интегральной суммы
Интегральной суммой для функции y=f(x) на
отрезке [a,b] называется сумма произведений длин элементарных отрезков ∆xi
на значения функции f(ci) в произвольных точках этих отрезков
Слайд 7
Определение определенного интеграла
Определенным интегралом от функции f(x) на
отрезке [a,b] называется предел (если он существует) интегральной суммы
для функции f(x) на отрезке [a,b], не зависящий от способа разбиения отрезка [a,b] и выбора точек ci, найденный при условии, что длины элементарных отрезков (включая и максимальный ∆xmax) стремятся к нулю.
Слайд 9
Основные свойства определенного интеграла
10 Величина определенного интеграла не
зависит от обозначения переменной интегрирования (инвариантность):
20 При перестановке пределов
интегрирования определенный интеграл меняет свой знак на обратный (перестановочность):
Слайд 10
Основные свойства определенного интеграла
30 Если промежуток интегрирования [a,b]
разбит на конечное число частичных промежутков, то определенный интеграл,
взятый по промежутку [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам (аддитивность):
Слайд 11
Основные свойства определенного интеграла
40 Определенный интеграл от алгебраической
суммы конечного числа непрерывных функций равен такой же алгебраической
сумме определенных интегралов от этих функций (линейность):
Слайд 12
Основные свойства определенного интеграла
50. Если подынтегральная функция f(x)
на отрезке интегрирования сохраняет постоянный знак, то определенный интеграл
представляет собой число того же знака, что и функция, при условии b>a (монотонность):если sgn(f(x))=const, то и sgn
= sgn(f(x)).
60. Модуль интеграла функции не превосходит интеграл от модуля функции (неравенство по модулю)
Слайд 13
Основные свойства определенного интеграла
70. Определенный интеграл от непрерывной
функции равен произведению значения этой функции в некоторой промежуточной
точке x=c отрезка интегрирования [a,b] на длину отрезка b-a (теорема о среднем значении функции):Значение f(c) называется средним значением функции на отрезке [a,b]
Слайд 15
Формула Ньютона-Лейбница.
Определенный интеграл равен разности значений первообразной подынтегральной
функции для верхнего и нижнего пределов интегрирования.
Слайд 17
Непосредственное интегрирование
Этот способ основан на использовании свойств определенного
интеграла, приведении подынтегрального выражения к табличной форме путем тождественных
преобразований и применении формулы Ньютона-Лейбница.Вычислить определенный интеграл:
.