- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Проблема четырех красок
Содержание
- 2. Цель работы:Изучить правила раскрашивания географических карт и опытно – экспериментальным путем проверить задачу четырёх красок
- 3. Задачи работы:1. Рассмотреть свойства плоских графов2.Изучить правила
- 4. Леонард Эйлер (1707 – 1783гг)
- 5. Задача о кёнигсбергских мостах
- 6. Граф к задаче о кёнигсбергских мостах Точки A, B,C,D - вершины графаЛинии – ребра графа
- 7. Свойства связного графаЧисло нечётных вершин графа всегда
- 8. Свойства связного графаГраф с более чем двумя
- 9. Свойства связного графаГраф только с двумя нечётными
- 10. Свойства связного графаГраф все вершины у которого
- 11. Формула Эйлера о плоском графеДля любого плоского
- 12. Граф который можно начертить одним росчерком называется
- 13. Эйлеровы графыГраф все вершины которого четные (
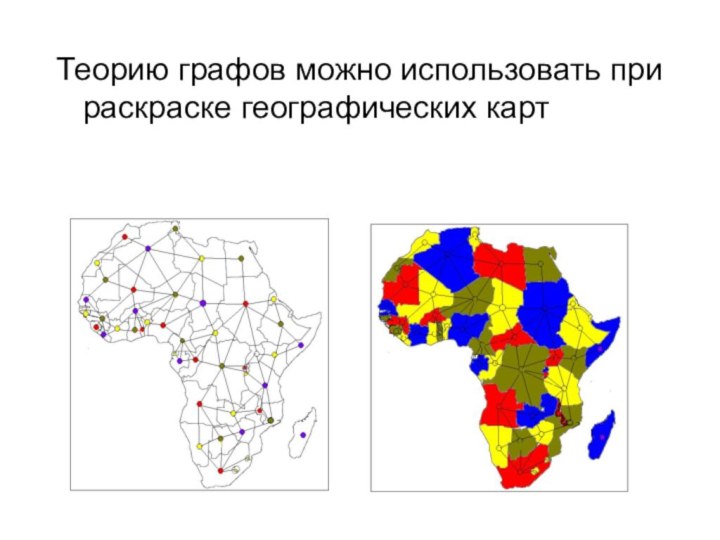
- 15. Теорию графов можно использовать при раскраске географических карт
- 16. Математическая задачаОпределить по чистой контурной карте минимального
- 17. Раскраска карты с помощью графовТерритории стран
- 18. Правила раскраски картыЕсли карта на плоскости представляет
- 19. Правила раскраски карты Если в каждой
- 20. Правила раскраски карты Карту Северной Америки
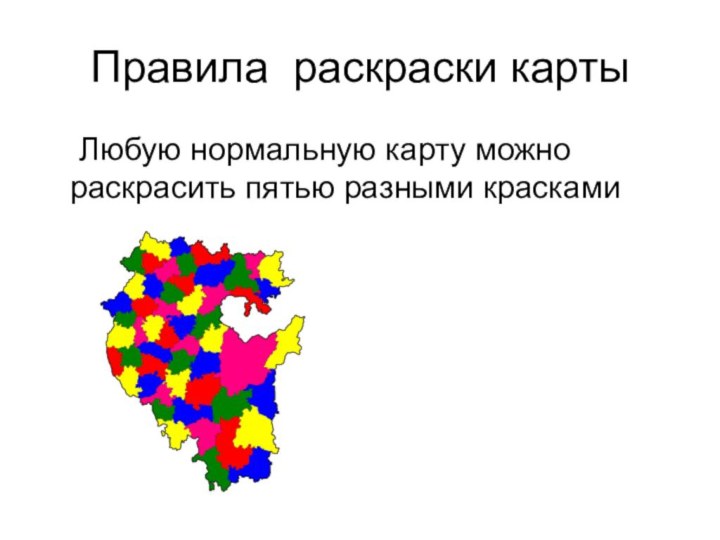
- 21. Правила раскраски карты Любую нормальную карту можно раскрасить пятью разными красками
- 22. Проблема четырёх красок — математическая задача,предложенная студентом лондоского университета Фрэнсис Гутри в 1852 году.
- 23. Гипотеза: «Выяснить, можно ли всякую расположенную на
- 24. Вершинная раскраска графа Вершины графа – страны
- 25. Проблема четырёх красок Карта Северной Америки в графах
- 26. Проблема четырех красокКарта Южной Америки в графах
- 27. Проблема четырех красокКарта Африки в графах
- 28. Проблема четырех красокКарта Африки
- 29. Проблема четырёх красокТакой способ вершинной раскраски графа называется «жадным алгоритмом», изучается в ВУЗах в дискретной математике.
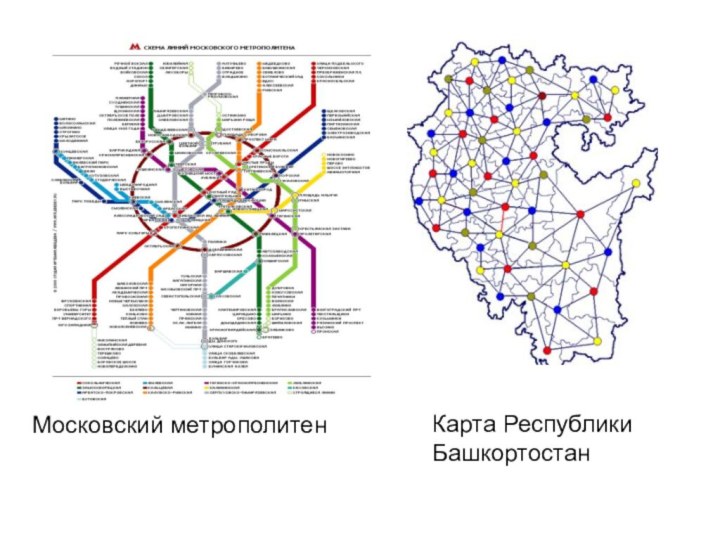
- 30. Чтобы покрасить карту Республики Башкортостан (состоит из 54 района) достаточно 4 краски
- 31. выводПравила раскраски географических карт можно применить на
- 32. * Правила раскраски географических карт можно применить
- 33. Скачать презентацию
- 34. Похожие презентации
Цель работы:Изучить правила раскрашивания географических карт и опытно – экспериментальным путем проверить задачу четырёх красок




























Слайд 2
Цель работы:
Изучить правила раскрашивания географических карт и опытно
– экспериментальным путем проверить задачу четырёх красок
Слайд 3
Задачи работы:
1. Рассмотреть свойства плоских графов
2.Изучить правила раскраски
графов
3.Раскраска географических карт с помощью графов
4.Разработка сборника головоломок
Слайд 7
Свойства связного графа
Число нечётных вершин графа всегда четно.
Невозможно начертить граф, который имел бы нечетное число нечетных
вершин
Слайд 8
Свойства связного графа
Граф с более чем двумя нечётными
вершинами невозможно начертить одним росчерком
(Решение задачи о кёнигсбергских
мостах)
Слайд 9
Свойства связного графа
Граф только с двумя нечётными вершинами
можно начертить одним росчерком, при этом движение нужно начать
с одной нечётной вершине и закончить в другой
Слайд 10
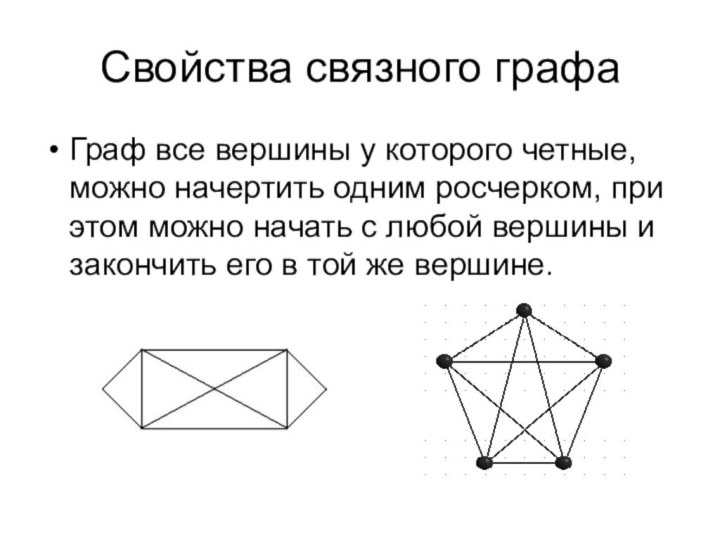
Свойства связного графа
Граф все вершины у которого четные,
можно начертить одним росчерком, при этом можно начать с
любой вершины и закончить его в той же вершине.
Слайд 11
Формула Эйлера о плоском графе
Для любого плоского графа
имеет место соотношение
В - Р + Г = 2
Слайд 12
Граф который можно начертить одним росчерком называется
уникурсальным
графом
Эскиз портрета Эйлера
Знак, состоящий из двух рогов Луны,
который Магомет
описывал однимросчерком
Слайд 13
Эйлеровы графы
Граф все вершины которого четные
( можно
начертить одним росчерком)
Эйлеровы графы применяются при составлении одностороннего
движения
в городе.
Слайд 16
Математическая задача
Определить по чистой контурной карте минимального числа
красок, с помощью которых можно правильно раскрасить данную карту.
Слайд 17
Раскраска карты
с помощью графов
Территории стран – грани
графа
Границы стран – ребра графа
Точки пересечения границ – вершины
графа
Слайд 18
Правила раскраски карты
Если карта на плоскости представляет собой
эйлеровый граф, то его можно раскрасить всего двумя красками.
Слайд 19
Правила раскраски карты
Если в каждой вершине
соответствующего карте графа сходятся три ребра, то такую карту
можно правильно раскрасить тремя красками в том и только в том случае, если каждая страна имеет четное число границ
Слайд 20
Правила раскраски карты
Карту Северной Америки
можно раскрасить
тремя красками,
если не учестьморя и океаны
Слайд 22
Проблема четырёх красок —
математическая задача,
предложенная
студентом лондоского университета Фрэнсис Гутри в 1852 году.
Слайд 23
Гипотеза:
«Выяснить, можно ли всякую
расположенную на сфере
карту
раскрасить четырьмя красками так,
чтобы любые две области,
имеющие
общий участокграницы, были раскрашены
в разные цвета»
Слайд 24
Вершинная раскраска графа
Вершины графа – страны
Ребра
– границы этих стран
Проблема четырёх красок :
Верно ли, что
хроматическое число любого графа,
расположенного на плоскости
не больше четырёх?
Слайд 29
Проблема четырёх красок
Такой способ вершинной раскраски графа называется
«жадным алгоритмом», изучается в ВУЗах в дискретной математике.
Слайд 31
вывод
Правила раскраски географических карт можно применить на уроках
географии. Я думаю, что задача правильной раскраски карты наименьшим
количеством цветов развивает мышление, способствует запоминанию названия странРаскраска графов широко применяется на практике. Например:
при составлений расписаний уроков для образовательных учреждений
расписания в спорте
планирование встреч, собраний, интервью;
расписания транспорта, в том числе — авиатранспорта
расписания для коммунальных служб.
Слайд 32 * Правила раскраски географических карт можно применить на
уроках географии. Задача правильной раскраски карты наименьшим количеством цветов
развивает мышление, способствует запоминанию названия стран.* После исследования уникурсального графа составлены задачи – головоломки, которые можно решать на факультативных занятиях по математике
* Раскраска графов широко применяется на практике. Например:
при составлений расписаний уроков для образовательных учреждений
расписания в спорте
планирование встреч, собраний, интервью;
расписания транспорта, в том числе — авиатранспорта
расписания для коммунальных служб.
Также раскраску графов можно использовать при решений судоку.





























