- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основы анализа данных. Регрессионный анализ. (Лекция 6)
Содержание
- 2. СекцииОпределения, термины и примеры примененияSergey MityaginВиды регрессионного анализаКоэффициенты регрессии и детерминацииЛинейная регрессия на корреляции
- 3. Примеры примененияSergey Mityagin1. Моделирование числа поступивших в
- 4. Связь между переменнымиSergey MityaginЛинейная положительная связьЛинейная отрицательная связьСвязь отсутствуетНелинейная связь
- 5. ОпределенияSergey MityaginРегрессионный анализ — статистический метод исследования влияния
- 6. ОпределенияSergey MityaginЦели регрессионного анализа1. Определение степени детерминированности
- 7. ТерминыSergey MityaginУравнение регрессии Математическая формула, применяемая к
- 8. ТерминыSergey MityaginФормирование уравнения регрессии – процедура минимизации случайного остатка. Выделение зависимых переменныхВыделение смещения мат.ожидания
- 9. ОпределенияSergey Mityagin
- 10. СекцииОпределения, термины и примеры примененияSergey MityaginВиды регрессионного анализаКоэффициенты регрессии и детерминацииЛинейная регрессия на корреляции
- 11. Виды регрессионного анализаSergey MityaginЛинейные по переменнымНе линейные по переменнымЛинейные по параметрамНе линейные по параметрам Не надо использовать
- 12. Линейный регрессионный анализSergey MityaginЗапись в матричной форме:
- 13. Линейный регрессионный анализSergey MityaginОценка параметров: Получаем в явном виде набор уравнений: МНК:
- 14. Линейный регрессионный анализSergey MityaginПример:XY
- 15. Линейный регрессионный анализSergey MityaginПример:XY
- 16. Линейный регрессионный анализSergey MityaginПример:XY Y=1,02*x+4,66
- 17. Линейный регрессионный анализSergey MityaginЗадание:XY
- 18. Другие виды регрессионного анализаSergey MityaginПолиномиальная функция регрессии: Запись в матричной форме:
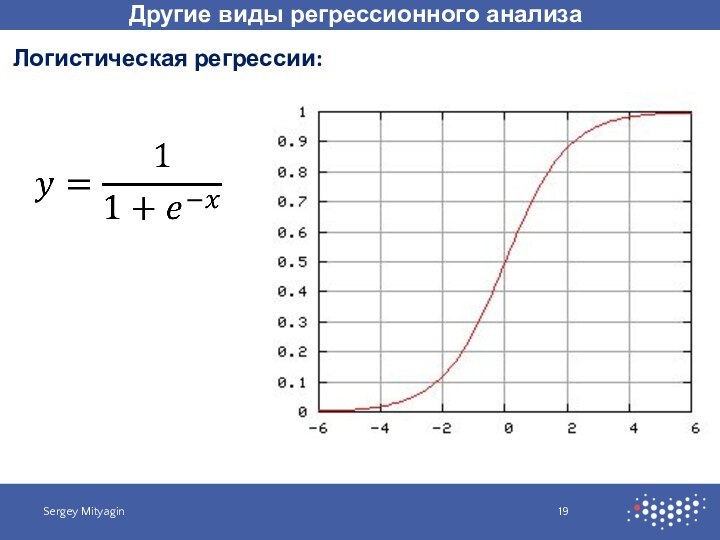
- 19. Другие виды регрессионного анализаSergey MityaginЛогистическая регрессии:
- 20. СекцииОпределения, термины и примеры примененияSergey MityaginВиды регрессионного анализаКоэффициенты регрессии и детерминацииЛинейная регрессия на корреляции
- 21. Смысл коэффициента регрессииSergey MityaginСвойства коэффициента регрессии• Коэффициент
- 22. Коэффициент детерминацииSergey MityaginКоэффициент детерминации рассматривают, как правило,
- 23. Достоинства и недостаткиSergey MityaginДостоинства:Недостатки:1. Простота вычислительных алгоритмов.2.
- 24. СекцииОпределения, термины и примеры примененияSergey MityaginВиды регрессионного анализаКоэффициенты регрессии и детерминацииЛинейная регрессия на корреляции
- 25. Линейная регрессия на корреляцииSergey MityaginЛинейная регрессия на
- 26. Скачать презентацию
- 27. Похожие презентации
СекцииОпределения, термины и примеры примененияSergey MityaginВиды регрессионного анализаКоэффициенты регрессии и детерминацииЛинейная регрессия на корреляции

























Слайд 2
Секции
Определения, термины
и примеры применения
Sergey Mityagin
Виды регрессионного анализа
Коэффициенты
регрессии
и детерминации
Слайд 3
Примеры применения
Sergey Mityagin
1. Моделирование числа поступивших в университет
для лучшего понимания факторов, удерживающих детей в том же
учебном заведении.2. Моделирование потоков миграции в зависимости от таких факторов как средний уровень зарплат, наличие медицинских, школьных учреждений, географическое положение.
3. Моделирование дорожных аварий как функции скорости, дорожных условий, погоды и т.д.,
4. Моделирование потерь от пожаров как функции от таких переменных как количество пожарных станций, время обработки вызова, или цена собственности.
Слайд 4
Связь между переменными
Sergey Mityagin
Линейная положительная связь
Линейная отрицательная связь
Связь
отсутствует
Нелинейная связь
Слайд 5
Определения
Sergey Mityagin
Регрессионный анализ — статистический метод исследования влияния одной
или нескольких независимых переменных X 1 , X 2
, . . . , X p на зависимую переменную Y .Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными.
Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.
Слайд 6
Определения
Sergey Mityagin
Цели регрессионного анализа
1. Определение степени детерминированности вариации
критериальной (зависимой) переменной предикторами (независимыми переменными).
2. Предсказание значения зависимой
переменной с помощью независимой(-ых).3. Определение вклада отдельных независимых переменных в вариацию зависимой.
Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
Слайд 7
Термины
Sergey Mityagin
Уравнение регрессии Математическая формула, применяемая к независимым
переменным, чтобы лучше спрогнозировать зависимую переменную, которую необходимо моделировать.
-
Коэффициенты регрессии- Зависимые переменные
- Ошибка регрессии
Неслучайная часть
Свободный коэф.
Случайный остаток
Слайд 8
Термины
Sergey Mityagin
Формирование уравнения регрессии – процедура минимизации случайного
остатка.
Выделение зависимых переменных
Выделение смещения мат.ожидания
Слайд 10
Секции
Определения, термины
и примеры применения
Sergey Mityagin
Виды регрессионного анализа
Коэффициенты
регрессии
и детерминации
Линейная регрессия на корреляции
Слайд 11
Виды регрессионного анализа
Sergey Mityagin
Линейные по переменным
Не линейные по
переменным
Линейные по
параметрам
Не линейные
по параметрам
Не надо использовать
Слайд 13
Линейный регрессионный анализ
Sergey Mityagin
Оценка параметров:
Получаем в явном виде
набор уравнений:
МНК:
Слайд 18
Другие виды регрессионного анализа
Sergey Mityagin
Полиномиальная функция регрессии:
Запись в
матричной форме:
Слайд 20
Секции
Определения, термины
и примеры применения
Sergey Mityagin
Виды регрессионного анализа
Коэффициенты
регрессии
и детерминации
Линейная регрессия на корреляции
Слайд 21
Смысл коэффициента регрессии
Sergey Mityagin
Свойства коэффициента регрессии
• Коэффициент регрессии
может принимать любые значения.
• Коэффициент регрессии не симметричен ,
т.е. изменяется, если X и Y поменять местами.• Единицей измерения коэффициента регрессии является отношение единицы измерения Y к единице измерения X: ([Y] / [X]).
• Коэффициент регрессии изменяется при изменении единиц измерения X и Y .
Например, результативный признак Y измеряется в рублях, а факторный признак X в количестве рабочих (чел.), то коэффициент регрессии измеряется в рублях на человека (руб. / чел.)
Слайд 22
Коэффициент детерминации
Sergey Mityagin
Коэффициент детерминации рассматривают, как правило, в
качестве основного показателя, отражающего меру качества регрессионной модели, описывающей
связь между зависимой и независимыми переменными модели. Коэффициент детерминации показывает, какая доля вариации объясняемой переменной y учтена в модели и обусловлена влиянием на нее факторов, включенных в модель:
Слайд 23
Достоинства и недостатки
Sergey Mityagin
Достоинства:
Недостатки:
1. Простота вычислительных алгоритмов.
2. Наглядность
и интерпретируемость
результатов (для линейной модели)
1. Невысокая точность прогноза
(в основном - интерполяция данных ). 2. Субъективный характер выбора вида конкретной зависимости (формальная подгонка модели под эмпирический материал).
3. Отсутствие объяснительной функции (невозможность объяснения причинно -следственной связи).
Слайд 24
Секции
Определения, термины
и примеры применения
Sergey Mityagin
Виды регрессионного анализа
Коэффициенты
регрессии
и детерминации
Линейная регрессия на корреляции
Слайд 25
Линейная регрессия на корреляции
Sergey Mityagin
Линейная регрессия на корреляции —
частный случай линейной регрессии. Применяется для построения простейших регрессионных
моделей для прогнозирования временных рядов.