- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основы математического моделирования систем
Содержание
- 2. ОСНОВЫ МЕТОДОЛОГИИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯЭтапы построения математической модели
- 3. Мathematical model an equation representing an idea
- 4. Изучение и сбор информации об объекте-оригинале Проводится
- 5. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИФормализация операций На основе
- 6. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИНа основании принятой математической
- 7. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИОпытные испытанияПолученная экспериментальная модель
- 8. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИАнализ полученных результатов Полученный
- 9. Корректировка модели ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИУточняются существенные
- 10. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИОптимизация моделиСущность оптимизации моделей
- 11. ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗАЧёрный ящик
- 12. ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО
- 13. Состояние системы S характеризуется векторамиПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗАСостояние системы
- 14. ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО
- 15. ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО
- 16. ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗАИмитационное моделирование
- 17. Имитационное моделированиеМетод статистических испытанийМетод Монте-Карло Суть его
- 18. Имитационное моделированиеМетод статистического моделирования
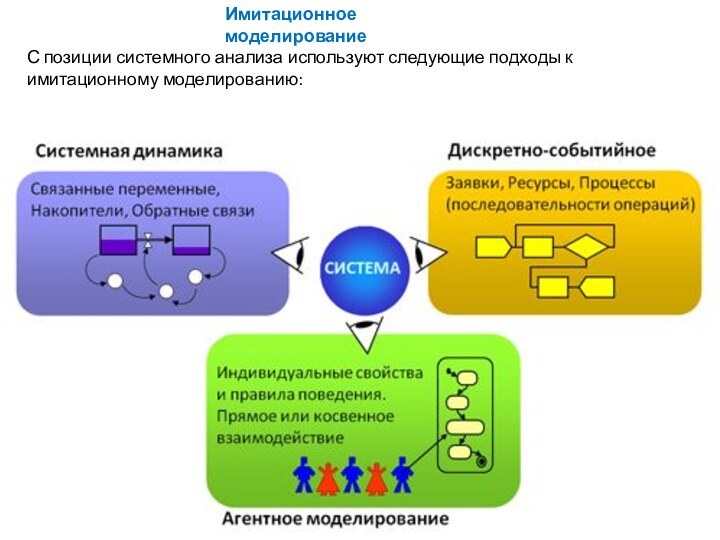
- 19. С позиции системного анализа используют следующие подходы к имитационному моделированию:Имитационное моделирование
- 20. Имитационное моделирование
- 21. Имитационное моделированиеподход к моделированию (или вид имитационного
- 22. Потоки - скорости изменения уровней. Например, потоки
- 23. Функции решений (вентили) - функции зависимости потоков
- 24. Имитационное моделированиеИмитационная модель физиологического процесса адаптации организма к изменяющимся внешним воздействиям
- 25. Имитационное моделированиегде (r) - функция, характеризующая производительность
- 26. Имитационное моделированиеm-код
- 27. Скачать презентацию
- 28. Похожие презентации

















Слайд 3
Мathematical model an equation representing an idea (http://www.cliffsnotes.com/Section/id-305499,articleId-57021.html)
ЭТАПЫ
ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
вырабатывается общий подход к исследуемой проблеме. Определяется основная цель моделирования и пути ее достижения. Выделяются задачи моделирования, в результате решения которых цель моделирования может быть достигнута. Осуществляется анализ или подбор подходящих гипотез, аналогий, теорий. В результате этого этапа возникает гипотетическая модель
Слайд 4
Изучение и сбор информации об объекте-оригинале
Проводится подробное
описание моделируемого объекта с позиций системного подхода. Осуществляется сбор
и обработка экспериментальных данных и данных наблюдений, их учет и систематизация. Выявляются возможные состояния системы. Для каждого из состояний определяются входные и выходные характеристики, определяются элементы системы и их свойства, взаимосвязи между элементами, строятся структура модели или моделей, если состояний системы несколько. Накладываются ограничения. Логически соединяют функции элементов и связывают их с состоянием системы в целом. Такое представление называется концептуальной моделью.ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Слайд 5
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Формализация операций
На основе концептуальной
модели, опираясь на цель моделирования и понимание природы исследуемой
системы, выделят существенные характеристики. Выделяют управляемые и неуправляемые параметры и производят символизацию. Опираясь на структурную схему системы, описывают связи между элементами объекта в виде математических выражений. Накладываются принятые ограничения на значения управляемых параметров. Формируется критерий эффективности и целевая функция. Полученное описание называют аналитической или математической моделью.
Слайд 6
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
На основании принятой математической модели
обосновывается метод ее решения с учетом знаний и предпочтений
пользователя и разработчика. Выбирается среда для решения вычислительных задач: ручные и/или машинные методы проектирования, расчета и исследований, стандартные аппаратные и программные средства. В случае необходимости применения уникальных приёмов обработки и анализа принимается решение о необходимости разработки специального программного обеспечения для выполнения системного анализа и синтеза модели системы. Планируется эксперимент. Реализуется алгоритмы и сценарии эксперимента. Принимается критерий оценки эффективности модели. На этом этапе создаётся экспериментальный образец модели или экспериментальная модель.Выбор метода решения
Слайд 7
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Опытные испытания
Полученная экспериментальная модель подвергается
проверочным испытаниям. Получают выборки данных в виде приращений параметров,
зависимостей выходных параметров от входных воздействий, результаты измерений внутренних параметров и другие характеристики. В результате этого этапа получают экспериментальный материал.
Слайд 8
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Анализ полученных результатов
Полученный экспериментальный
материал сопоставляется предполагаемым показателям. Проводится оценка адекватности и погрешности
моделирования. Проверочный процесс является итеративным. В случае неудовлетворительных результатов проверки адекватности переходят к этапу корректировки модели. В случае удовлетворительных результатов принимается решение о возможности ее практического использования. Уточнение модели происходит до тех пор, пока не будут получены приемлемые результаты. Заключения о состоятельности проверки не носят формального характера, поскольку основываются на опыте и интуиции исследователя. Опытные испытания и анализ полученных результатов составляют экспериментальную проверку модели, которая позволяет выявить грубые ошибки
Слайд 9
Корректировка модели
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Уточняются существенные параметры,
ограничения на значения управляемых параметров, связи и критерий эффективности.
После внесения изменений в модель снова осуществляется экспериментальная проверка.
Слайд 10
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Оптимизация модели
Сущность оптимизации моделей состоит
в их упрощении при заданном уровне адекватности.
Этот этап не
является обязательным. .
Слайд 12
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗА
Динамическая
модель системы
Статическая модель системы
представляет собой отображение между двумя подмножествами
свойств моделируемого объекта Y и {X, V, Н}, что в векторной форме может быть записано какТакие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состояниями системы
Слайд 13
Состояние системы S характеризуется векторами
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ
С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗА
Состояние системы
Слайд 14
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗА
Моделирование
статических систем
Пример: Пронаблюдаем за изменением температуры некоторого гипотетического больного.
Пусть врач ставит задачу определить момент выздоровления по данным изменения температуры больного за время лечения в медицинском стационаре. Результаты ежедневных измерений температуры представлены на графике Статическое моделирование объединяет множество моделей, которые отражают характеристики реальных систем таких, что сколь угодно длительное рассматриваемое в эксперименте внешнее воздействие не оказывает влияние на их характеристики. Такие системы и соответственно их модели называют системами (моделями) «без памяти».
Задача состоит в том, чтобы, зная множество значений на входах [x] и выходах [y], построить модель, то есть определить функцию ящика h. Одним из методов решения такой задачи может быть регрессионный анализ.
Поскольку для врача важна именно тенденция изменения температуры, то вполне можно принять зависимость между входом и выходом линейной. Таким образом, для пациента принята гипотеза связи выходных и входных данных y(i) = ax(i) + b. Дальнейшие расчёты должны позволить определить параметры линейной модели a и b.
Слайд 15
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗА
Моделирование
динамических систем
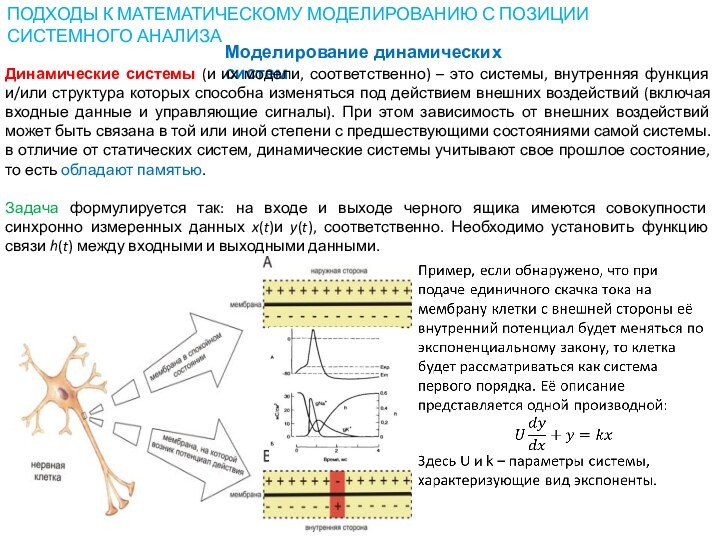
Динамические системы (и их модели, соответственно) – это
системы, внутренняя функция и/или структура которых способна изменяться под действием внешних воздействий (включая входные данные и управляющие сигналы). При этом зависимость от внешних воздействий может быть связана в той или иной степени с предшествующими состояниями самой системы. в отличие от статических систем, динамические системы учитывают свое прошлое состояние, то есть обладают памятью.Задача формулируется так: на входе и выходе черного ящика имеются совокупности синхронно измеренных данных x(t)и y(t), соответственно. Необходимо установить функцию связи h(t) между входными и выходными данными.
Слайд 16
ПОДХОДЫ К МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ С ПОЗИЦИИ СИСТЕМНОГО АНАЛИЗА
Имитационное
моделирование
Слайд 17
Имитационное моделирование
Метод статистических испытаний
Метод Монте-Карло
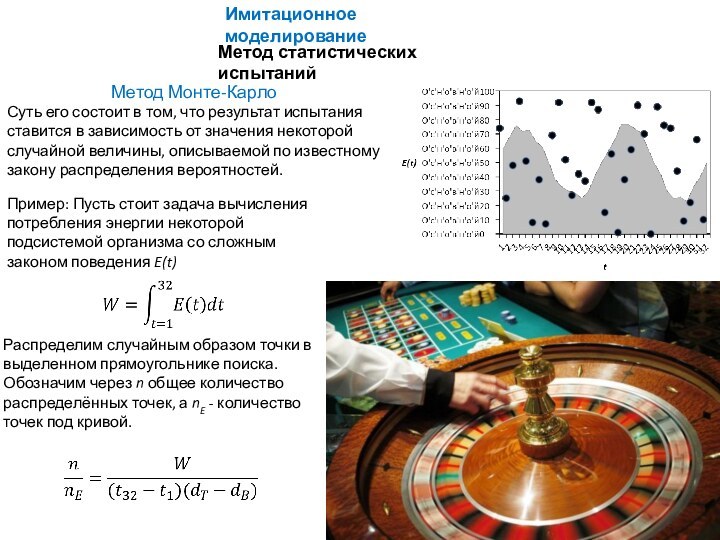
Суть его состоит
в том, что результат испытания ставится в зависимость от
значения некоторой случайной величины, описываемой по известному закону распределения вероятностей.Пример: Пусть стоит задача вычисления потребления энергии некоторой подсистемой организма со сложным законом поведения E(t)
Распределим случайным образом точки в выделенном прямоугольнике поиска. Обозначим через n общее количество распределённых точек, а nE - количество точек под кривой.
Слайд 19 С позиции системного анализа используют следующие подходы к
имитационному моделированию:
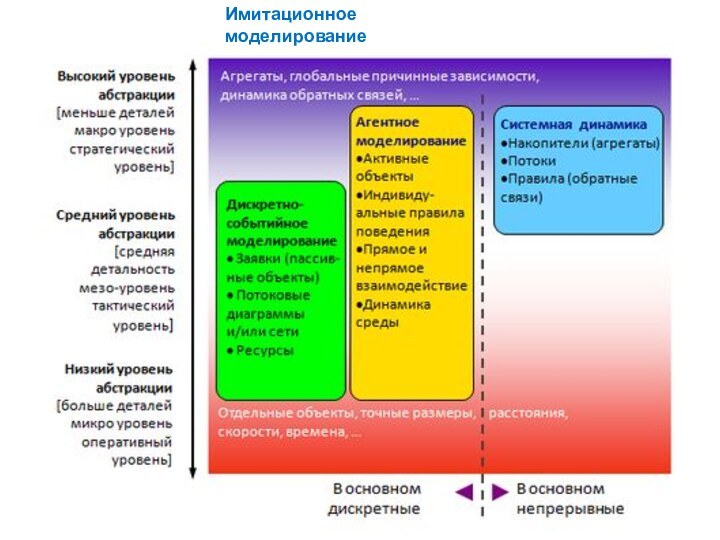
Имитационное моделирование
Слайд 21
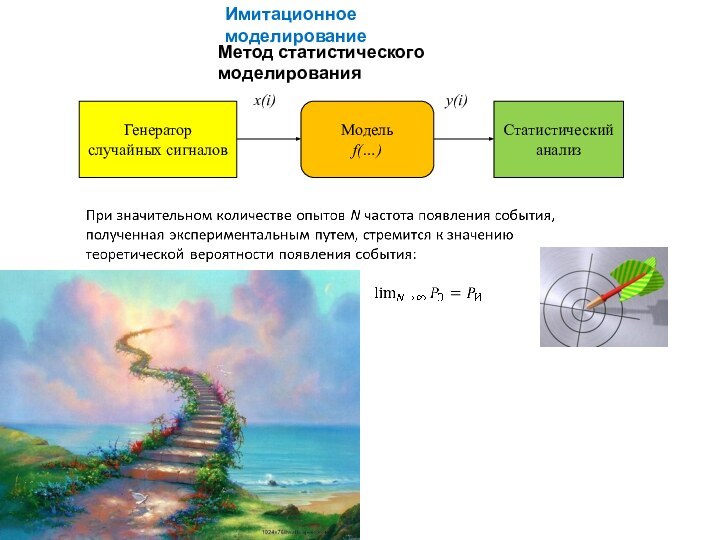
Имитационное моделирование
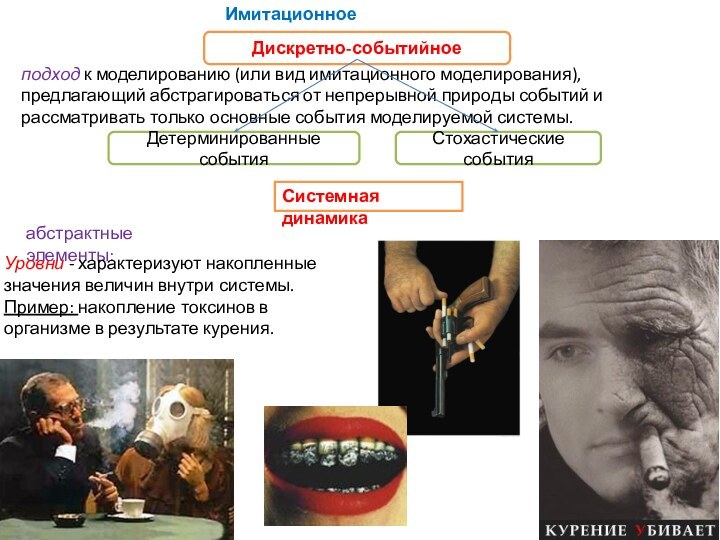
подход к моделированию (или вид имитационного моделирования),
предлагающий абстрагироваться от непрерывной природы событий и рассматривать только
основные события моделируемой системы.Дискретно-событийное
Детерминированные события
Стохастические события
Системная динамика
абстрактные элементы:
Уровни - характеризуют накопленные значения величин внутри системы.
Пример: накопление токсинов в организме в результате курения.
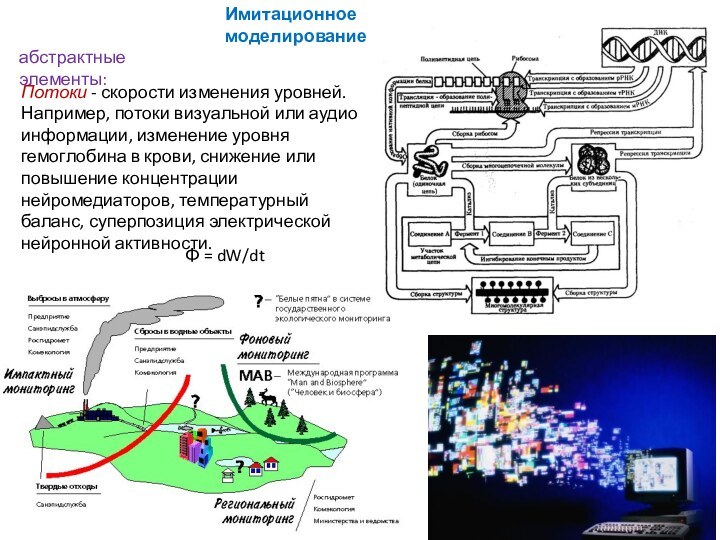
Слайд 22 Потоки - скорости изменения уровней. Например, потоки визуальной
или аудио информации, изменение уровня гемоглобина в крови, снижение
или повышение концентрации нейромедиаторов, температурный баланс, суперпозиция электрической нейронной активности.Имитационное моделирование
абстрактные элементы:
Φ = dW/dt
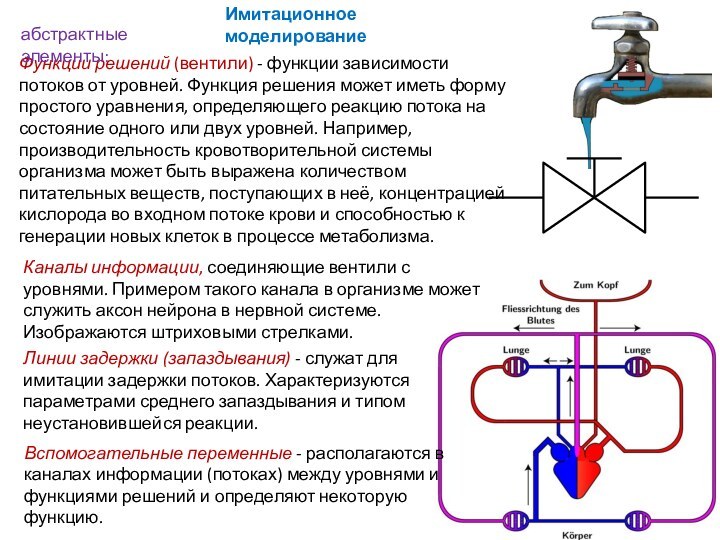
Слайд 23 Функции решений (вентили) - функции зависимости потоков от
уровней. Функция решения может иметь форму простого уравнения, определяющего
реакцию потока на состояние одного или двух уровней. Например, производительность кровотворительной системы организма может быть выражена количеством питательных веществ, поступающих в неё, концентрацией кислорода во входном потоке крови и способностью к генерации новых клеток в процессе метаболизма.Имитационное моделирование
абстрактные элементы:
Каналы информации, соединяющие вентили с уровнями. Примером такого канала в организме может служить аксон нейрона в нервной системе. Изображаются штриховыми стрелками.
Линии задержки (запаздывания) - служат для имитации задержки потоков. Характеризуются параметрами среднего запаздывания и типом неустановившейся реакции.
Вспомогательные переменные - располагаются в каналах информации (потоках) между уровнями и функциями решений и определяют некоторую функцию.
Слайд 24
Имитационное моделирование
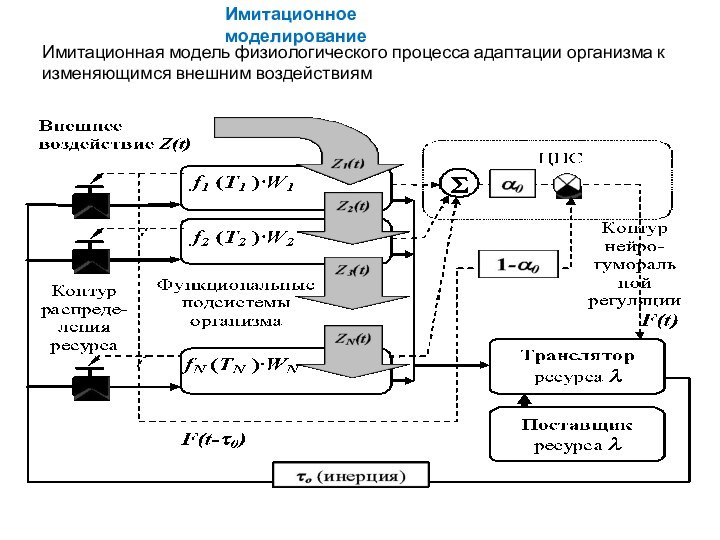
Имитационная модель физиологического процесса адаптации организма к
изменяющимся внешним воздействиям
Слайд 25
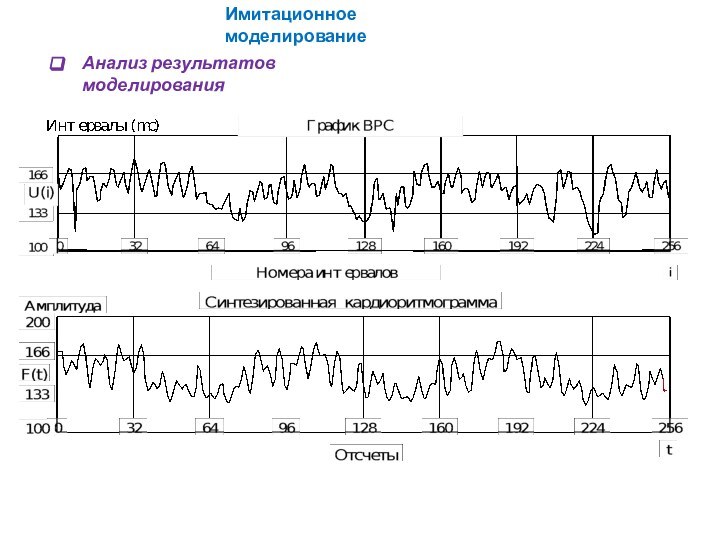
Имитационное моделирование
где (r) - функция, характеризующая производительность ресурса
r системы;
Формализация
Wi - i‑й весовой коэффициент в
S-м устойчивом состоянии; fi(Ti) - i- я функция вынуждающего воздействия подсистемы с циклом Ti;
0 - время задержки реакции (инерция) системы;
N - число подсистем формирующих воздействие;
Z(t) – функция воздействия.
Поведение модели полностью задается набором весовых коэффициентов на множестве {Wi}.