алгебры и геометрии требуются для решения задач на построение
геометрических фигур на компьютере, и разработать алгоритмы для решения задач на построение.Ц Е Л Ь Р А Б О Т Ы
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть














Ц Е Л Ь Р А Б О Т Ы
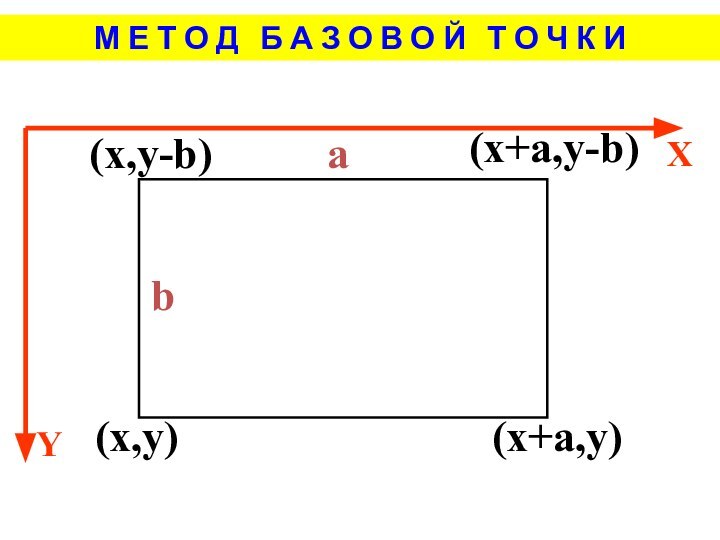
М Е Т О Д Ы
X
Y
A(X;Y)
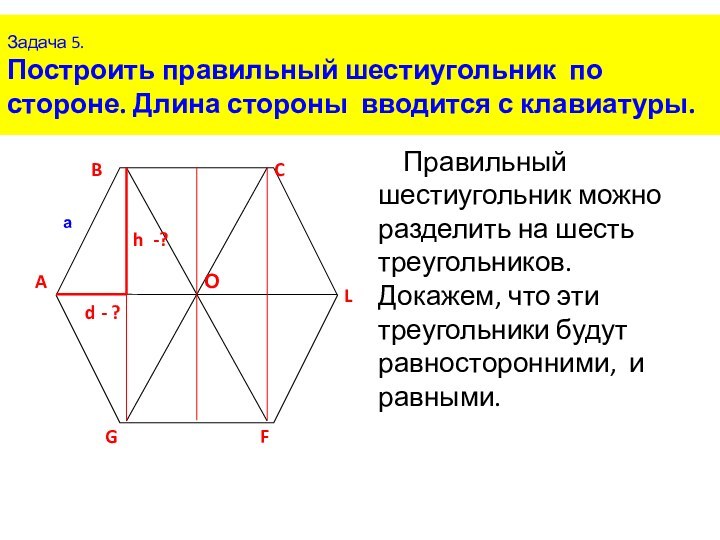
З А Д А Ч И НА П О С Т Р О Е Н И Е
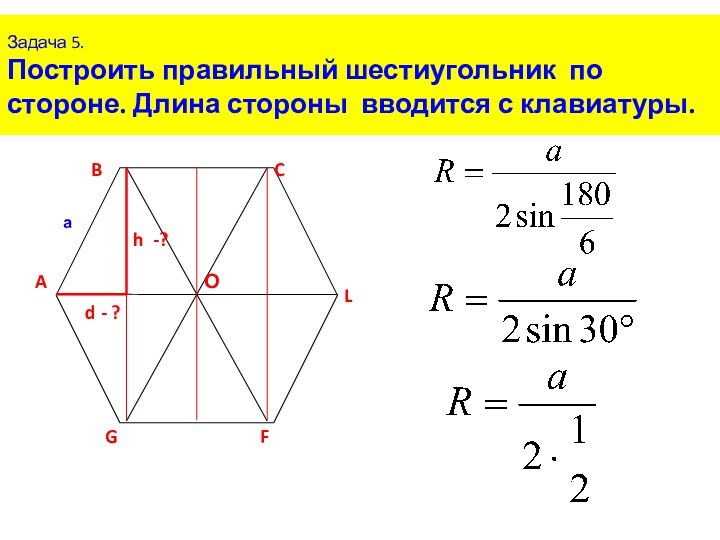
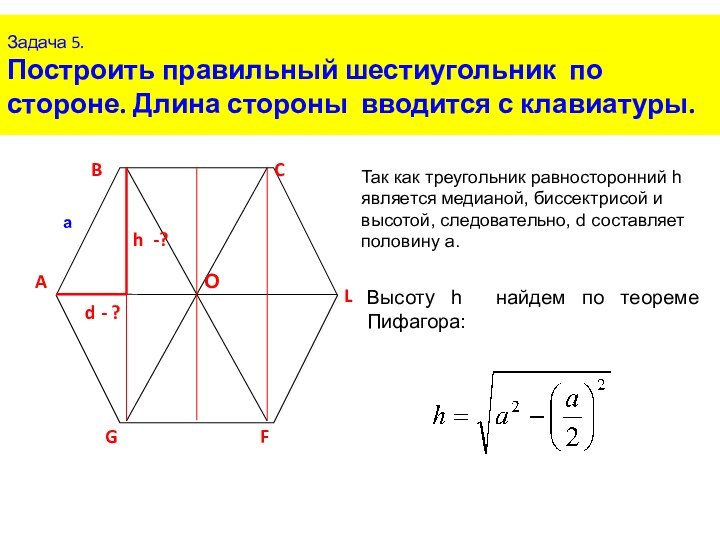
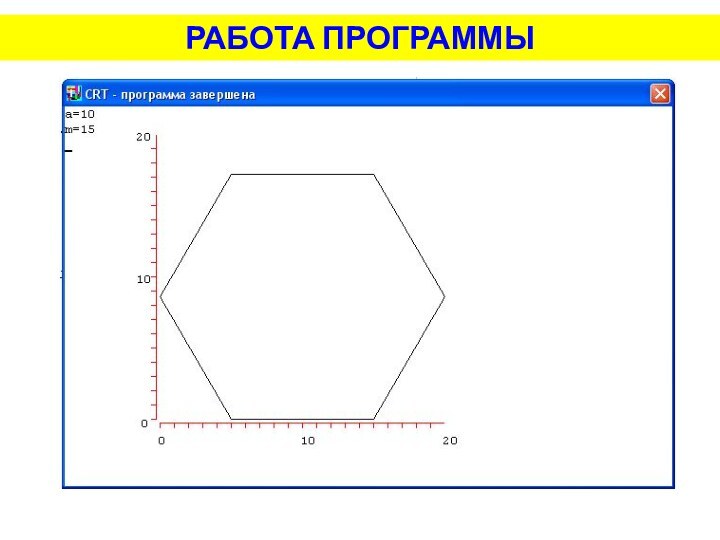
, где a=AB, n=6
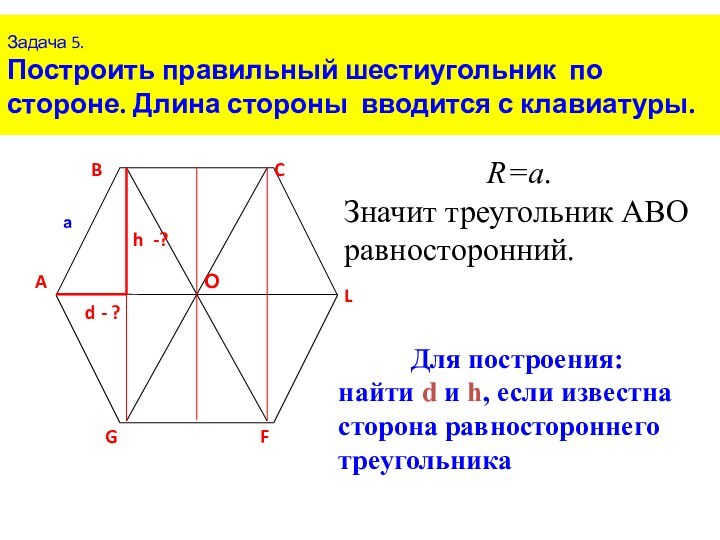
Так как треугольник равносторонний h является медианой, биссектрисой и высотой, следовательно, d составляет половину a.
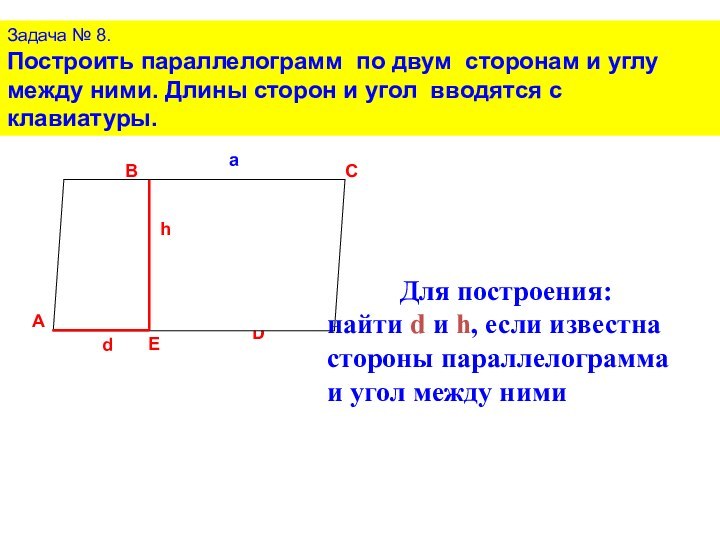
Для построения:
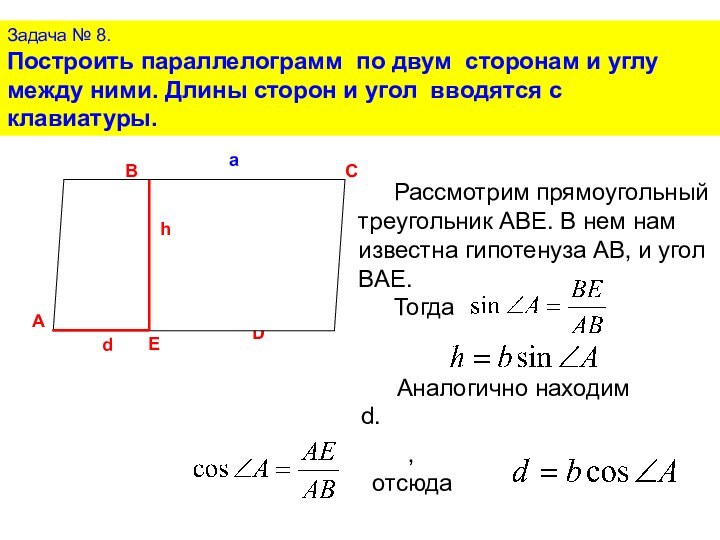
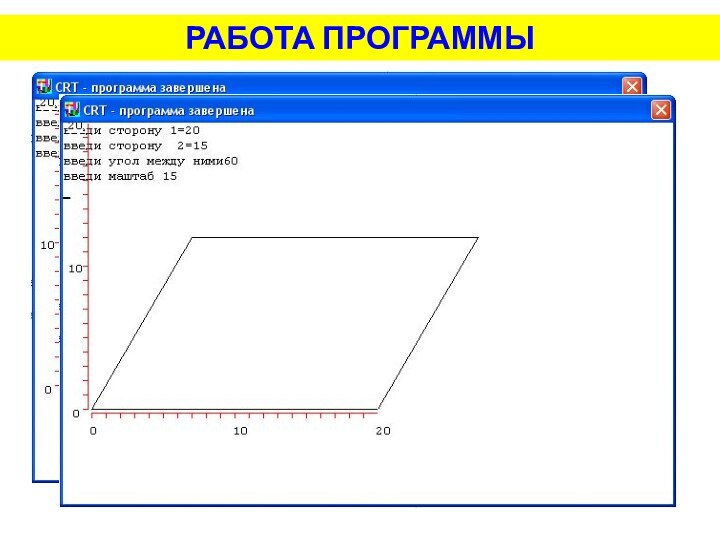
найти d и h, если известна стороны параллелограмма и угол между ними
Рассмотрим прямоугольный треугольник ABE. В нем нам известна гипотенуза АВ, и угол BAE.
Тогда
Аналогично находим d.
, отсюда
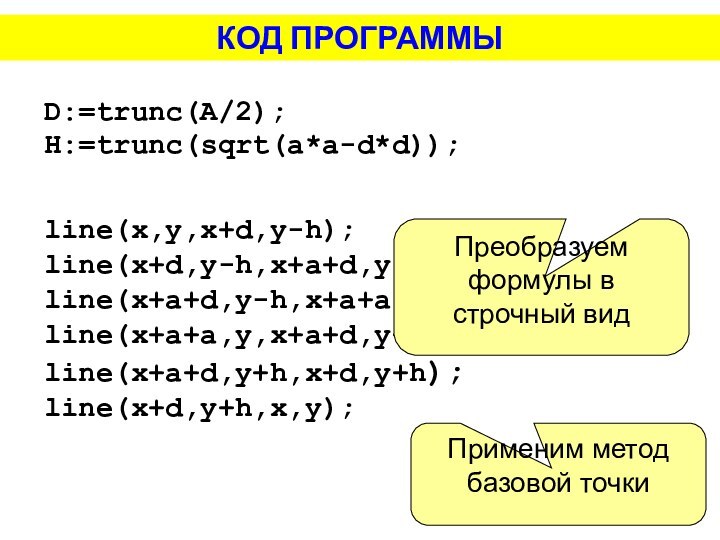
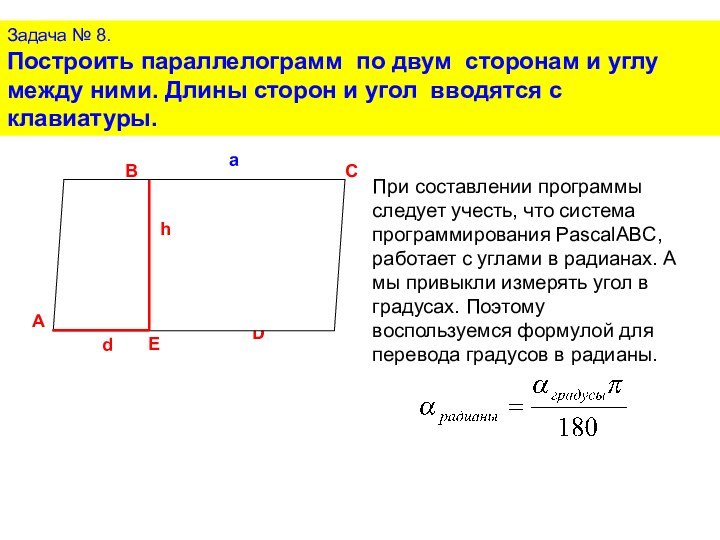
При составлении программы следует учесть, что система программирования PascalABC, работает с углами в радианах. А мы привыкли измерять угол в градусах. Поэтому воспользуемся формулой для перевода градусов в радианы.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами
Теорема о медиане равнобедренного треугольника. Медиана, проведённая к основанию в равнобедренном треугольнике, является высотой и биссектрисой
Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Противоположные стороны параллелограмма попарно равны.
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Синус угла - это отношение длины противоположного этому углу катета к гипотенузе
Косинус угла - это отношение прилежащего этому углу катета к гипотенузе
… а для остальных задач,
еще 31 правило и определение!
В Ы В О Д