- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллельность прямых и плоскостей - зачет
Содержание
- 2. Цели урока:Повторить теоретический материал главы «Параллельность прямых
- 3. Структура урока:Постановка цели урокаБуквенный диктантТест №1Тест №2Подведение итогов урока
- 4. Буквенный диктант 1. Две непересекающиеся
- 5. 4. Количество прямых, проходящих через точку
- 6. 8. Количество прямых, проходящих через одну
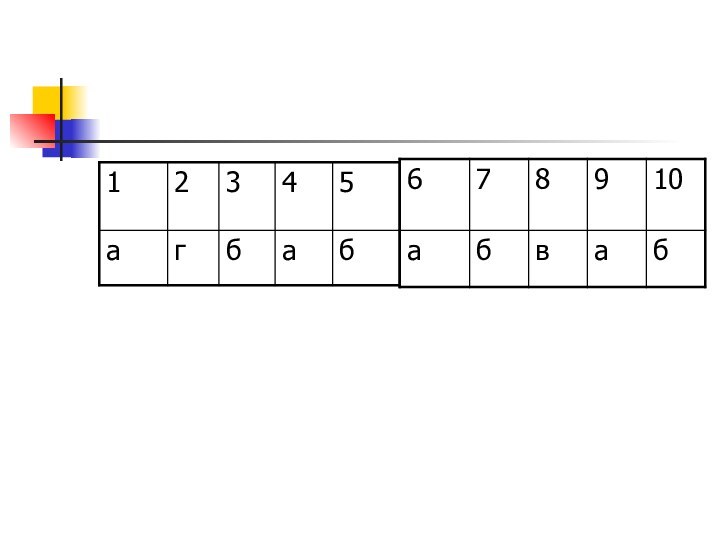
- 7. 1.параллелные2.лемма3.фигура4.одна5.скрещивающиеся6.плоскость7.стереометрия8.много9.тетраэдр10.признак
- 8. 1.Какое число сторон может иметь сечение
- 9. 4.Каково взаимное расположение прямых в пространстве,
- 10. 6. Чему равен угол между параллельными
- 11. 9.Угол между пересекающимися прямыми?а) меньший б)
- 14. Задача №2. На ребрах DA, DB и
- 15. Скачать презентацию
- 16. Похожие презентации
Цели урока:Повторить теоретический материал главы «Параллельность прямых и плоскостей».Проверить усвоение темы в ходе зачета.Формирование у учащихся потребности применения знаний в последующем.














Слайд 2
Цели урока:
Повторить теоретический материал главы «Параллельность прямых и
плоскостей».
применения знаний в последующем.
Слайд 4
Буквенный диктант
1. Две непересекающиеся прямые
в пространстве и лежащие в одной плоскости.
2. Теорема,
имеющая значение не столько сама по себе, сколько для дополнения других.3. Любое множество точек.
Слайд 5 4. Количество прямых, проходящих через точку вне
данной прямой, параллельно ей.
5. Прямые, которые не пересекаются
и не лежат в одной плоскости.6. Основная фигура в пространстве.
7. Раздел геометрии, в котором изучаются фигуры в пространстве.
Слайд 6
8. Количество прямых, проходящих через одну точку.
9. Поверхность, составленная из четырех треугольников.
10. Теорема, более
полно характеризующая случаи взаимного расположения фигур в пространстве.
Слайд 7
1.параллелные
2.лемма
3.фигура
4.одна
5.скрещивающиеся
6.плоскость
7.стереометрия
8.много
9.тетраэдр
10.признак
Слайд 8
1.Какое число сторон может иметь сечение тетраэдра?
а) 3,4 б) 4,5 в)
4 г) 3.2. Какое число сторон может иметь сечение параллелепипеда?
а) 3,4 б) 4,5,6 в)5,6 г) 3,4,5,6.
3. Используя признак параллельности плоскостей в кубе, укажите число пар параллельных плоскостей.
а) 3 б) 2 в) 1 г) 4.
Слайд 9 4.Каково взаимное расположение прямых в пространстве, если
они лежат в одной плоскости и имеют одну общую
точку?а) пересекаются б) параллельны
в) скрещиваются г) совпадают.
5. Сколько пар ребер, лежащих на скрещивающихся прямых, имеет тетраэдр?
а) 0 б) 1 в) 3 г) 2
Слайд 10
6. Чему равен угол между параллельными прямыми?
а) 00 б) 900 в) 450
г) 18007. Как называется плоскость, по обе стороны от которой имеются точки тетраэдра (параллелепипеда?)
а) α б) сечение в) β г) не знаю
8.Количество прямых, проходящих через две точки?
а) 2 б) много в) 1 г) 0.
Слайд 11
9.Угол между пересекающимися прямыми?
а) меньший б) 00
в) больший г)развернутый.
10.Что является пересечением секущей плоскости и
граней многогранника? а) точки б) отрезки в) прямые г) лучи.