называются параллельными, если они не пересекаются.
a bd c, m c d m
m
a
b
c
d
Параллельность отрезков, лучей.
Параллельность отрезка и прямой, отрезка и луча,
луча и прямой.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллельные прямые
Содержание
- 2. Определение параллельных прямыхДве прямые на
- 3. Углы при двух прямых, пересеченных
- 4. Признаки параллельности двух
- 5. Теорема 2 Если при пересечении
- 8. Аксиома параллельных прямыхЧерез точку, не
- 10. Теоремы об углах, образованных двумя параллельными прямыми
- 11. Следствие:Если прямая перпендикулярна к одной из двух
- 12. решение задачПрактические
- 13. Скачать презентацию
- 14. Похожие презентации
Определение параллельных прямыхДве прямые на плоскости называются параллельными, если они не пересекаются. a
Слайд 2
Определение параллельных прямых
Две прямые на плоскости
называются параллельными, если они не пересекаются.
a bd c, m c d m
m
Слайд 3 Углы при двух прямых, пересеченных
третьей
с ∩ ( a; b)
ے3 и ے 5; ے 4 и ے6 - накрест лежащие
углы
ے 4 и ے 5: ے 3 и ے 6 – односторонние
углы
ے 1 и ے 5; ے 4 и ے 8; ے 2 и ے 6 ; ے 3 и ے7 - соответственные углы
ТЕОРЕМА1 Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
а
b
с
1
2
3
4
5
6
7
8
Прямая «с» секущая
a и b – прямые
Слайд 4 Признаки параллельности двух
прямых
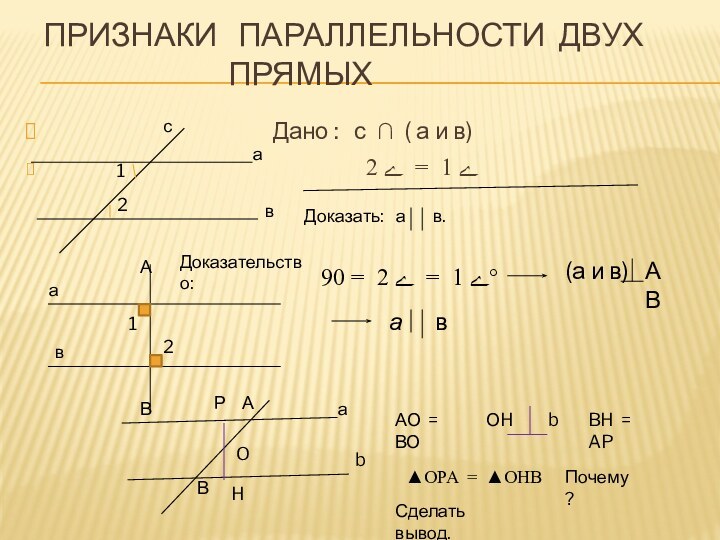
Дано : с ∩ ( а и в)
ے 1 = ے 2
с
а
в
1
2
Доказать: а в.
1
2
Доказательство:
ے 1 = ے 2 = 90°
А
В
а
в
(а и в)
АВ
а
в
а
А
В
Р
H
O
АО = ВО
ОH b
b
BH = AP
▲OPA = ▲OHB
Почему?
Сделать вывод.
Слайд 5 Теорема 2 Если при пересечении двух
прямых секущей соответственные углы равны , то прямые
параллельны Дано: с ∩ (а; b) ے 1 = ے 2
ے 1 + ے 2 = 180°
b
a
c
1
2
3
4
Доказать : а ║ b
Теорема 3:
Если при пересечении двух прямых секущей
сумма односторонних углов равна 180 °, то
прямые параллельны.
Дано:
с ∩ (а; b)
Доказать: а ║ b
Слайд 7 аксиомы
планиметрии
Через любые две точки проходит прямая, и притом
только одна.На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
От любого луча в заданную сторону можно отложить угол ,
равный данному неразвёрнутому углу, и притом только один.
А
В
d
(A, B) Є d
Слайд 8
Аксиома параллельных прямых
Через точку, не лежащую
на данной прямой проходит только одна прямая, параллельная
данной.. А Є m A Є t
А
m
t
t ║ m
•
Слайд 10 Теоремы об углах, образованных двумя параллельными прямыми и
секущей
Теорема:
Если две параллельные прямые пересечены секущей,
то накрест лежащие углы равны
а
b
c
Дано : с ∩ ( а ║ b )
1
2
ے 1 и ے 2 накрест лежащие
Доказать :
ے 1 = ے 2
Доказательство от противного:
ے 1 = ے 2
предположим, что
А
Построим ے 3 = ے 2
3
d
Как?
d ║ b почему?
Получили, что через точку А проходят две прямые ( а и d ) ║ b.
Но это противоречит аксиоме параллельных прямых.
Значит, допущение неверно.
ے 1 = ے 2
Ч.т.д.
Слайд 11
Следствие:
Если прямая перпендикулярна к одной из двух
параллельных
прямых, то она перпендикулярна и другой.
а
b
c
1
2
Дано:
а ║ b c ﬩ а Доказать:
c ﬩ а
Теорема:
Если две параллельные прямые пересечены секущей,
то соответственные углы равны
Дано : с ∩ ( а ║ b )
1
2
3
ے 1 и ے 2 - соответственные углы
ے 1 = ے 2
Доказать:
Если две параллельные прямые пересечены секущей,
то сумма односторонних углов равна 180°
Теорема:
1
2
с
а
b
a
b
c
Дано : с ∩ ( а ║ b )
ے 1 и ے 2 - односторонние
Доказать:
ے 1 + ے 2 = 180°
3
