- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллельные прямые в пространстве
Содержание
- 2. Параллельные прямыев пространстве
- 3. «Ни одно человеческое исследование не может называться
- 4. Параллельные прямыев пространстве
- 5. Цели урока:Рассмотреть взаимное расположение двух прямых в
- 6. Вспомним планиметрию1) Какие прямые называются параллельными?Параллельные прямые-
- 7. a || b3) Как через точку A,
- 8. a || b4) Сколько таких параллельных прямых можно провести?Вспомним планиметриюАПочему только одну?
- 9. 5) Аксиома параллельностиВспомним планиметриюЧерез точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
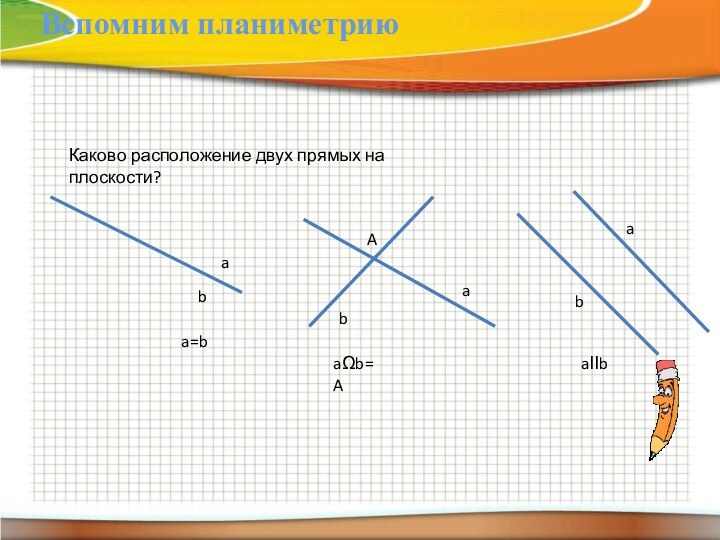
- 10. Каково расположение двух прямых на плоскости?abbaaba=baΩb=AAaІІbВспомним планиметрию
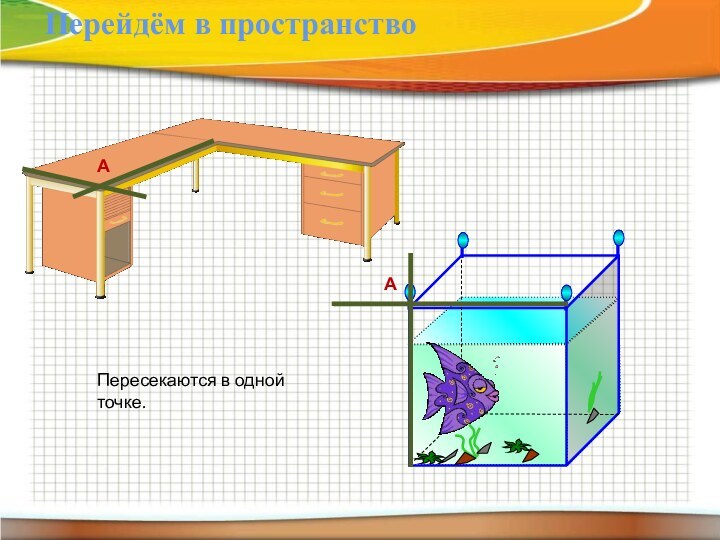
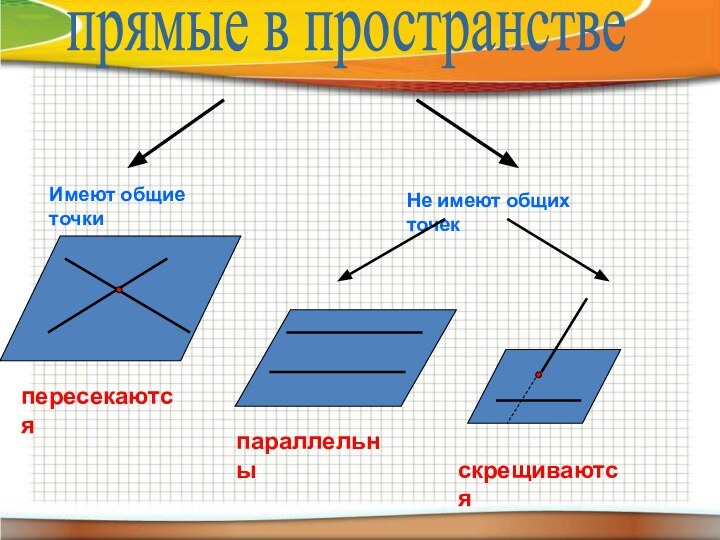
- 11. Перейдём в пространствоААПересекаются в одной точке.
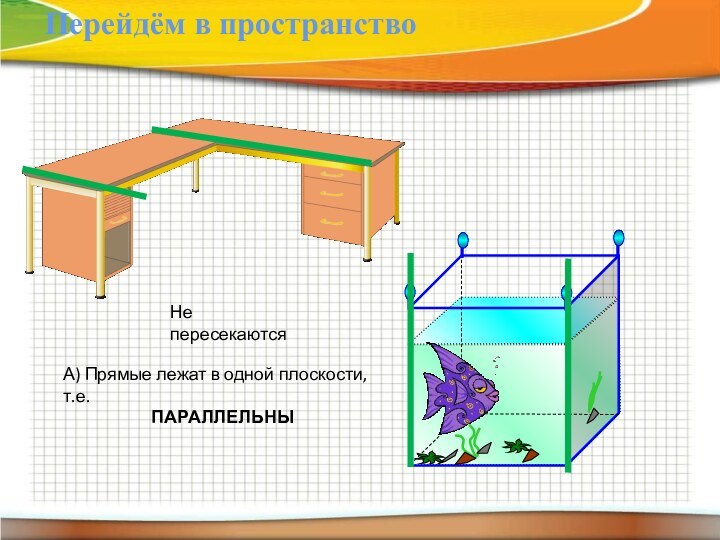
- 12. Перейдём в пространствоНе пересекаютсяА) Прямые лежат в одной плоскости, т.е. ПАРАЛЛЕЛЬНЫ
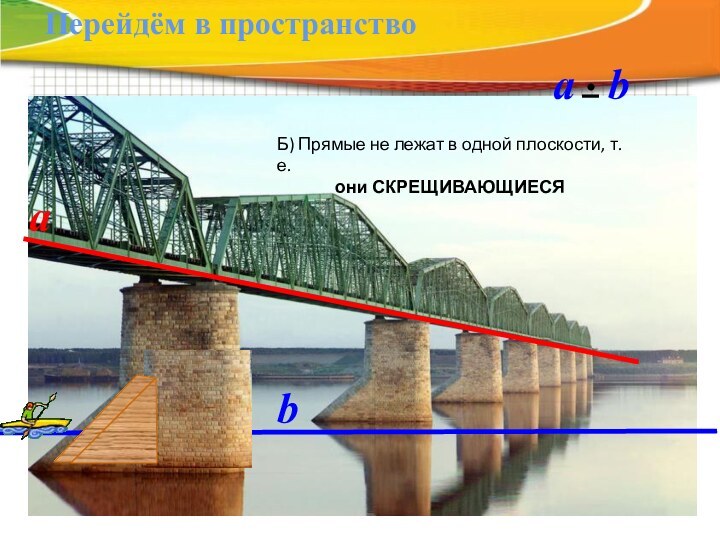
- 13. abПерейдём в пространствоБ) Прямые не лежат в одной плоскости, т.е. они СКРЕЩИВАЮЩИЕСЯ
- 14. прямые в пространстве
- 15. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIiНаглядное представление о скрещивающихся прямых дают две
- 17. Определение:Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
- 18. Через точку вне данной прямой в пространстве
- 19. Доказательство теоремы По теореме Через прямую и
- 20. Доказательство теоремы следовательно прямая b единственна.Теорема доказана.аАαПо
- 21. ЛеммаЕсли одна из двух параллельных прямых пересекает
- 22. ЛеммаЕсли одна из двух параллельных прямых пересекает
- 23. признак параллельностипрямых в пространстве.Если две прямые параллельны
- 24. Доказательство теоремы1. Если a, b, c лежат
- 25. Закрепление изученного материалаЗадача № 17DBCAMNPQДано:М- середина BD,N-
- 26. Домашнее задание:Пункт 4-5, теоремы, задача № 16
- 27. Скачать презентацию
- 28. Похожие презентации













Слайд 3 «Ни одно человеческое исследование не может называться истинной
наукой, если оно не прошло через математические доказательства»
Леонардо да Винчи
Слайд 5
Цели урока:
Рассмотреть взаимное расположение
двух прямых в пространстве;
Ввести понятие параллельных
и скрещивающихся прямых
2) Доказать теоремы о
параллельности прямых и параллельности трех прямых;
3) Закрепить эти понятия на моделях куба, призмы. пирамиды
Слайд 6
Вспомним планиметрию
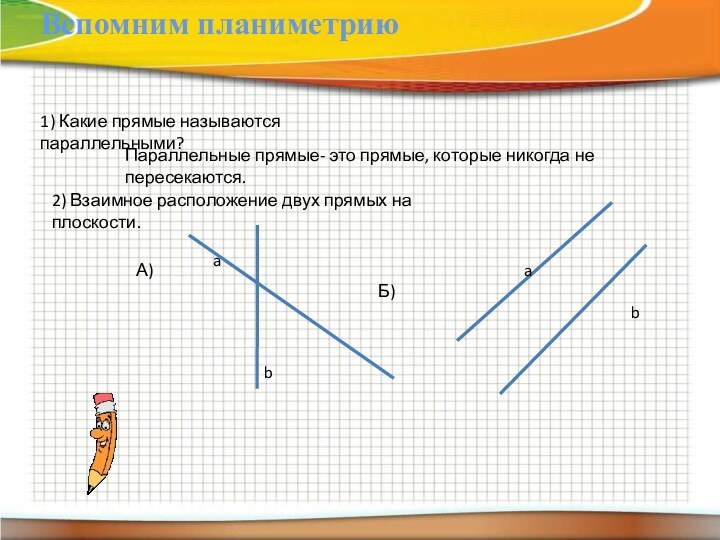
1) Какие прямые называются параллельными?
Параллельные прямые- это
прямые, которые никогда не пересекаются.
2) Взаимное расположение двух прямых
на плоскости.
Слайд 7
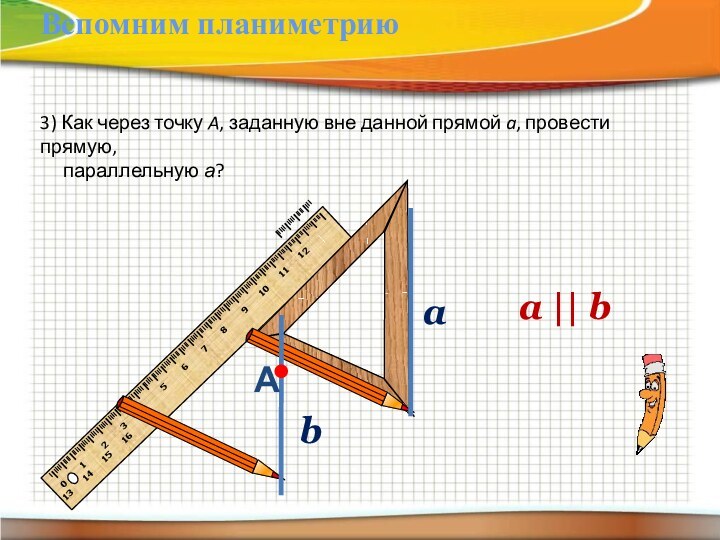
a || b
3) Как через точку A, заданную
вне данной прямой a, провести прямую,
параллельную а?Вспомним планиметрию
А
Слайд 8
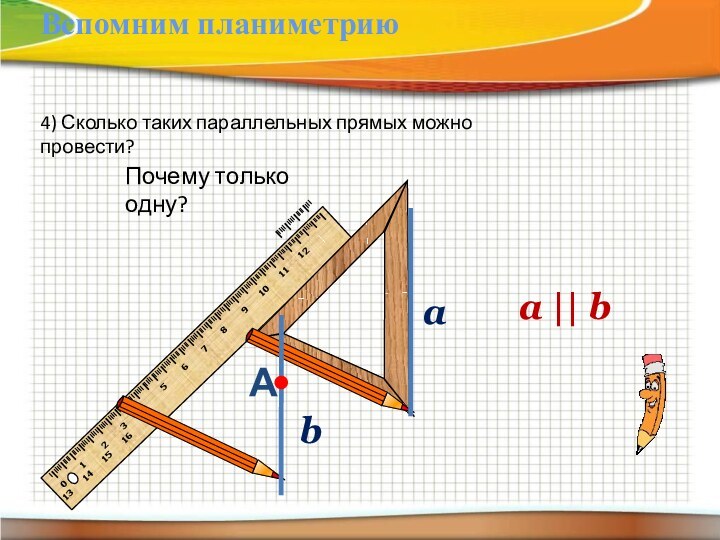
a || b
4) Сколько таких параллельных прямых можно
провести?
Вспомним планиметрию
А
Почему только одну?
Слайд 9
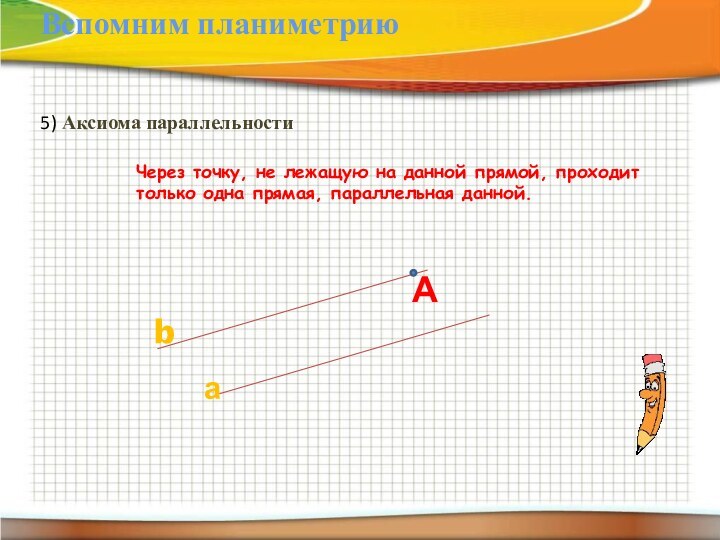
5) Аксиома параллельности
Вспомним планиметрию
Через точку, не лежащую на
данной прямой, проходит только одна прямая, параллельная данной.
Слайд 15
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
Наглядное представление о скрещивающихся прямых дают две дороги,
одна из которых проходит по эстакаде, а другая под
эстакадой.
Слайд 17
Определение:
Две прямые в пространстве называются параллельными,
если они
лежат в одной плоскости и не пересекаются.
Слайд 18 Через точку вне данной прямой в пространстве можно
провести прямую параллельную данной и притом только одну.
Дано:
прямая
а,А Є а
Доказать :
Провести через А пряму b || a,
b единственна
Теорема
Слайд 19
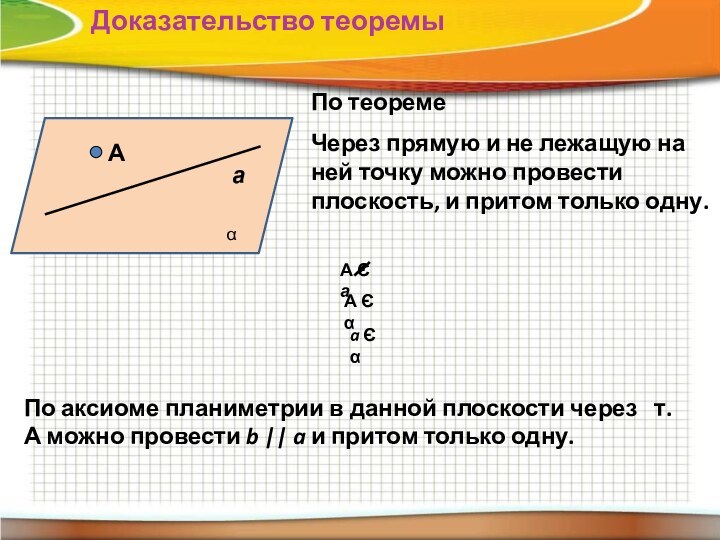
Доказательство теоремы
По теореме
Через прямую и не
лежащую на ней точку можно провести плоскость, и притом
только одну.А
а
α
А Є а
А Є α
a Є α
По аксиоме планиметрии в данной плоскости через т. А можно провести b || a и притом только одну.
Слайд 20
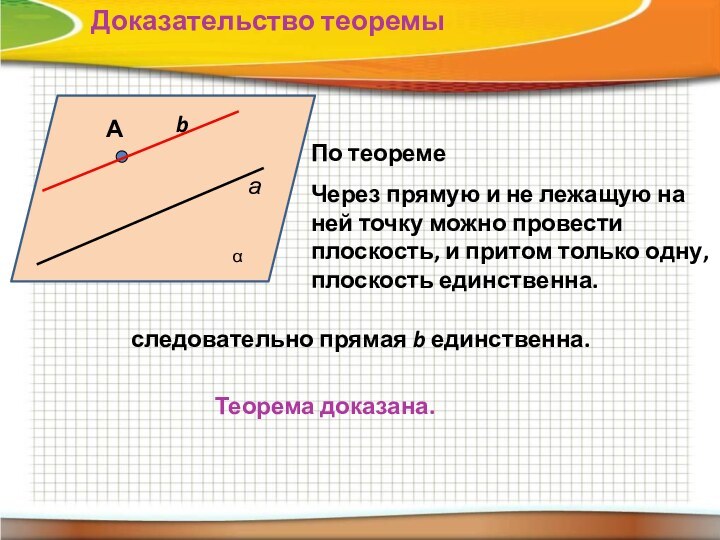
Доказательство теоремы
следовательно прямая b единственна.
Теорема доказана.
а
А
α
По теореме
Через прямую и не лежащую на ней точку можно
провести плоскость, и притом только одну, плоскость единственна.
Слайд 21
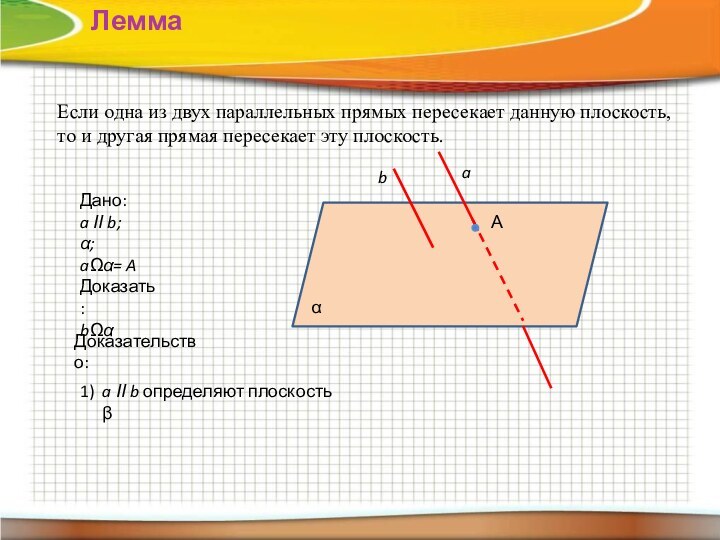
Лемма
Если одна из двух параллельных прямых пересекает данную
плоскость,
то и другая прямая пересекает эту плоскость.
Дано:
a ІІ
b;α;
aΩα= A
Доказать :
bΩα
α
a
b
А
Доказательство:
1)
a ІІ b определяют плоскость β
Слайд 22
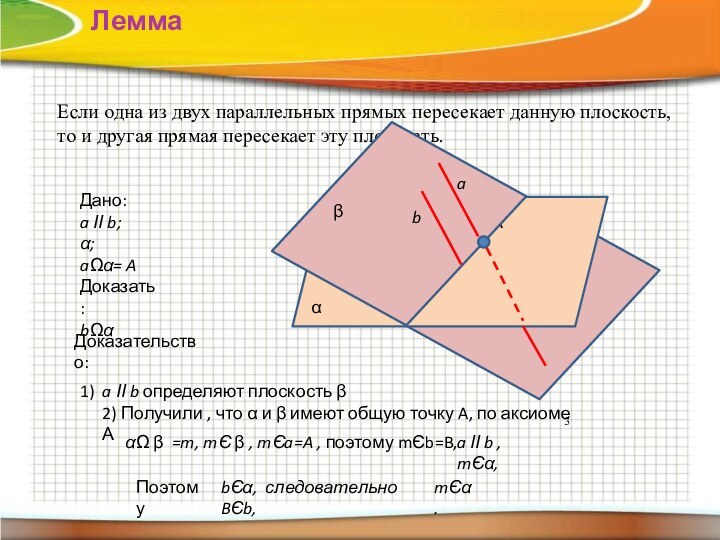
Лемма
Если одна из двух параллельных прямых пересекает данную
плоскость,
то и другая прямая пересекает эту плоскость.
Дано:
a ІІ
b;α;
aΩα= A
Доказать :
bΩα
Доказательство:
1)
a ІІ b определяют плоскость β
2) Получили , что α и β имеют общую точку A, по аксиоме А
α
a
b
А
a
b
β
3
αΩ β =m, mЄ β , mЄa=A , поэтому mЄb=B,
a ІІ b , mЄα,
Поэтому
bЄα, следовательно BЄb,
mЄα.
Слайд 23
признак параллельности
прямых в пространстве.
Если две прямые параллельны третьей
прямой, то они тоже параллельны
Дано: а||b; c||b
Доказать : a||c
Теорема
16.2
Слайд 24
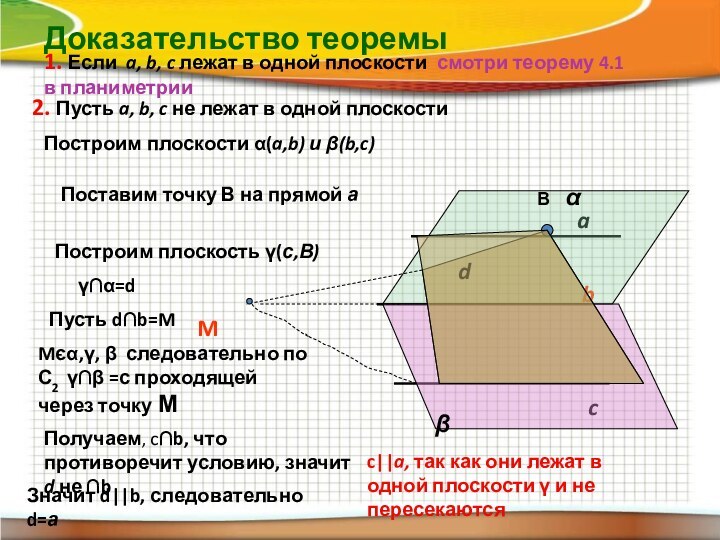
Доказательство теоремы
1. Если a, b, c лежат в
одной плоскости смотри теорему 4.1 в планиметрии
Mєα,γ, β следовательно
по С2 γ∩β =с проходящей через точку М Получаем, c∩b, что противоречит условию, значит d не ∩b
c||a, так как они лежат в одной плоскости γ и не пересекаются
Слайд 25
Закрепление изученного материала
Задача № 17
D
B
C
A
M
N
P
Q
Дано:
М- середина BD,
N- середина
CD,
Q- середина AC,
P- середина AB,
AD= 12,
DC= 14
Найти: P
MNPQ
Решение:
1. MNІІ
BC по составу средней линии MN II PQ; PQ IIDA
2. PMIIAD по составу средней линии
PMIIQN; NQIIDA
3. По определению MNQP -параллелограмм
4. PQ=7; PM= 6
P = 2(7+6)=26
MNPQ
Ответ: 26