Презентация на тему Пирамида by Сухотерин 9М

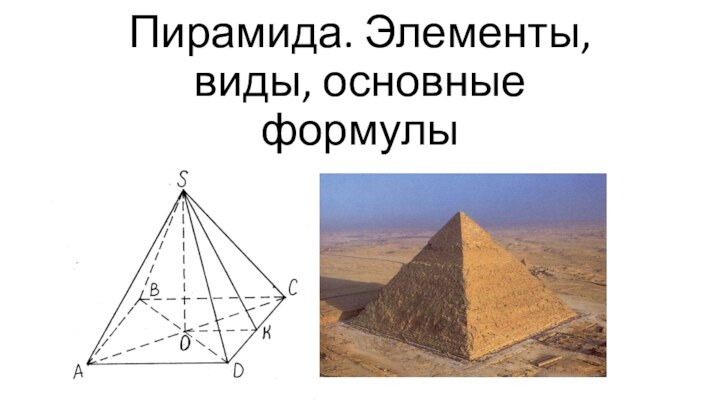
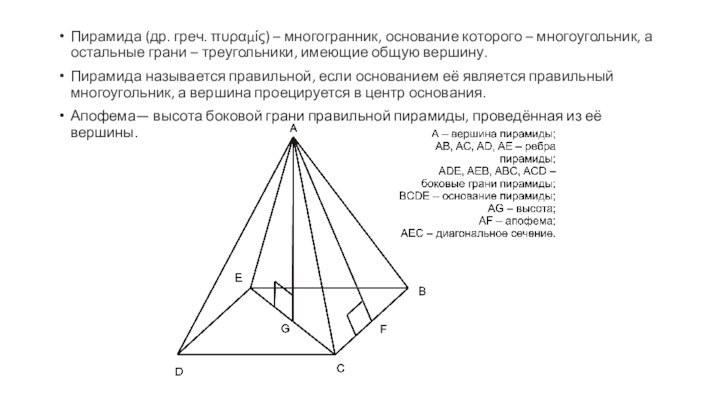
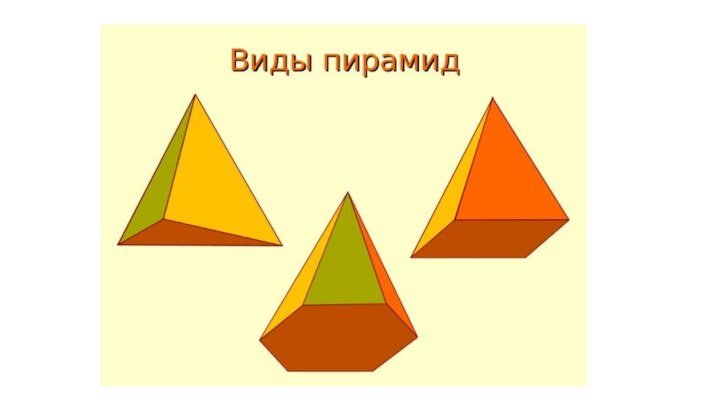
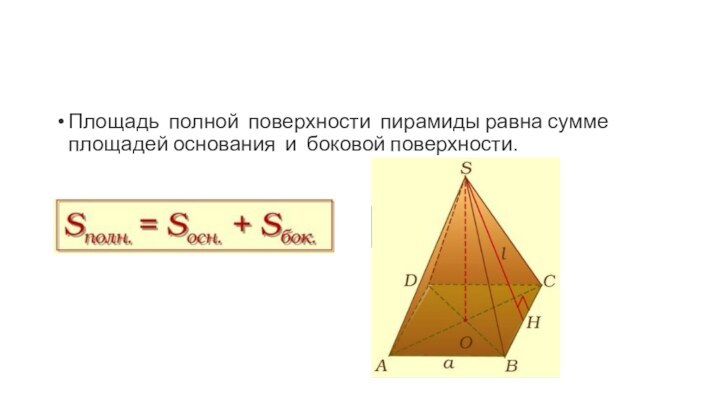
– многоугольник, а остальные грани – треугольники, имеющие общую

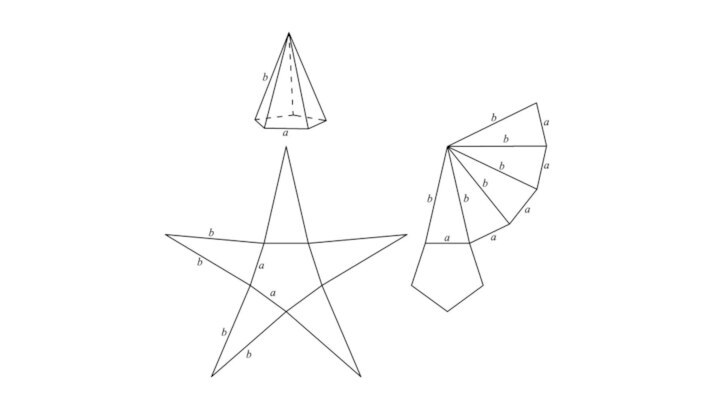
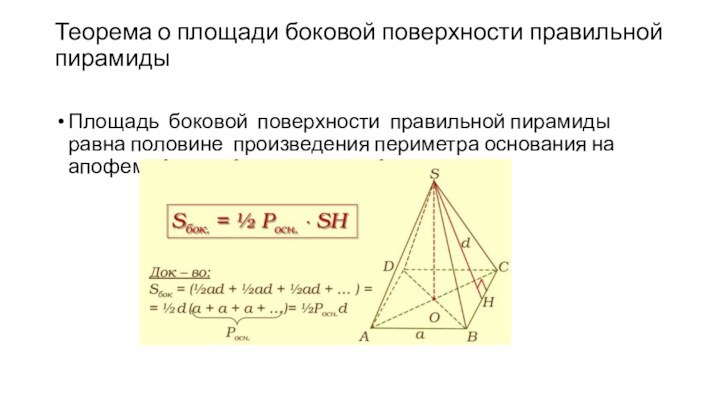
вершину.
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
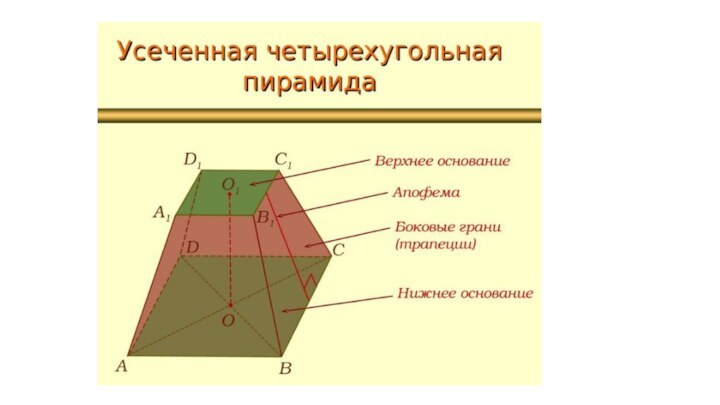
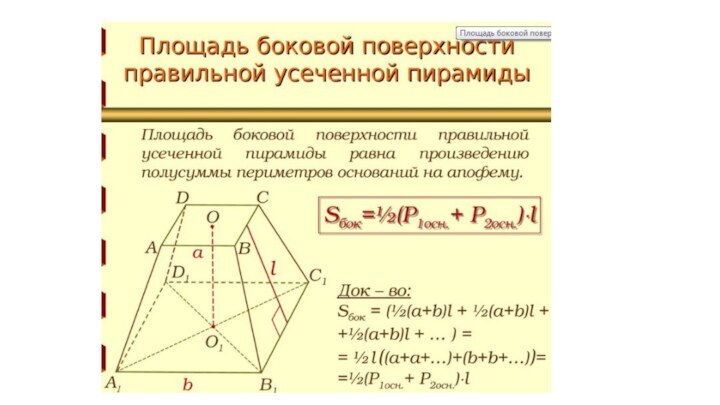
Апофема— высота боковой грани правильной пирамиды, проведённая из её вершины.

боковые рёбра равны, то:
вокруг основания пирамиды можно описать окружность,

причём вершина пирамиды проецируется в её центр;
боковые рёбра образуют с плоскостью основания равные углы;
также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
высоты боковых граней равны;
площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

и боковой поверхности.

S — площадь основания и h — высота;


где Vp

— объём параллелепипеда;

по формуле:

где a1,a2 — скрещивающиеся рёбра , d— расстояние

между a1 и a2 , α — угол между а1 и а2;

можно использовать формулы:



где a — апофема , P —

периметр основания, n — число сторон основания, b — боковое ребро, α— плоский угол при вершине пирамиды.

поверхности правильной пирамиды равна половине произведения периметра основания на

апофему.