Слайд 2
Цели урока
Образовательные:
1. Познакомить учащихся с числом π.
2.
Вывести формулы для нахождения длины окружности и
площади круга.
Развивающие:
1.Развивать познавательную активность, творческие
способности, смекалку и сообразительность.
2. Развивать логическое мышление, память, внимание и
речь.
Воспитательные:
1.Формировать коммуникативные умения учащихся.
2.Способствовать воспитанию уважительного отношения друг к другу при работе в группах, аккуратности при выполнении работы, уважения к ответам одноклассников.
Слайд 3
Задачи урока:
1. Актуализировать знания об
окружности, ее элементах.
2. Повторить правило округления
чисел.
3. Отработать умение решать текстовые
задачи на применение формул.
4. Продолжить формирование умений
учащихся работать в группе.
Слайд 4
Планируемые результаты
- Предметные результаты
Метапредметные
Личностные
Слайд 5
Этапы урока
Организационный момент. Мотивация
учебной деятельности учащихся
II. Актуализация опорных знаний
Усвоение
новых знаний. Практическая
работа
IV. Физкультминутка
V. Закрепление новых знаний
VI. Информация о домашнем задании,
инструктаж по его выполнению
Подведение итогов урока,
рефлексия
Слайд 6
Организационный момент. Мотивация
учебной деятельности учащихся
Загадки
Ни угла, ни стороны,
У круга есть одна подруга,
А родня – одни блины. Знакома всем ее наружность!
(круг) Она идет по краю круга
И называется -…(окружность)
Ребусы
Д "
П +
Ш=Щ
(площадь)
(длина)
Слайд 7
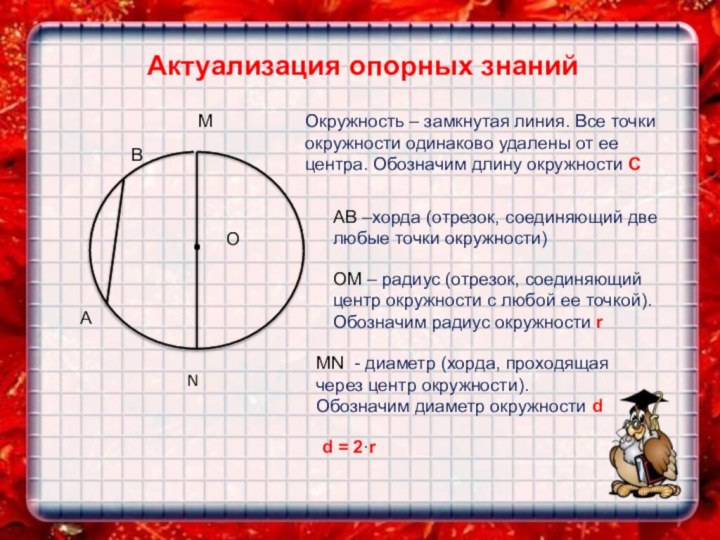
А
В
О
М
N
Окружность – замкнутая линия. Все точки окружности одинаково
удалены от ее центра. Обозначим длину окружности С
АВ –хорда
(отрезок, соединяющий две любые точки окружности)
ОМ – радиус (отрезок, соединяющий центр окружности с любой ее точкой). Обозначим радиус окружности r
MN - диаметр (хорда, проходящая через центр окружности).
Обозначим диаметр окружности d
d = 2·r
Актуализация опорных знаний
.
Слайд 8
Актуализация опорных знаний
Что называется отношение двух величин?
Как округлить
десятичную дробь до десятых, до сотых?
Округлить до десятых (до
сотых)
I II III
8,3153 8,5355 8,8298
3,2711 3,4366 3,2818
Слайд 9
Практическая работа
Измерение длины окружности
1. Обведите в тетрадях модели
кругов.
2. Обмотайте нитку вокруг наших моделей, а потом распрямите
нить .
3. Обмотайте нить по нарисованной в тетради окружности (длина нити должна быть равна этой окружности). Попросите помощи у товарища.
4. Измерьте длину нити линейкой.
5. Запишите результаты в тетрадь.
Измерение диаметра окружности
Проведите в окружностях диаметры.
Измерьте длину диаметров линейкой.
Запишите результаты в тетрадь.
Запишите отношение длины окружности к диаметру
Сосчитайте каждое отношение и округлите до сотых.
Слайд 11
Усвоение новых знаний
Число Архимеда π ≈ 22/7
π
≈ 3,1416 «Что я знаю о круге»
Длина окружности C = πd
C = 2πr, т.к. d=2r
Про площадь круга говорят:
Она равна пи эр квадрат. S = πr²
Слайд 12
Физкультминутка
Из-за парт мы выйдем дружно,
Но шуметь совсем не
нужно,
Встали прямо, ноги вместе,
Поворот кругом на месте.
Хлопнем пару раз
в ладошки.
И по топаем немножко.
А теперь представим, детки,
Будто руки наши – ветки.
Покачаем ими дружно,
Словно ветер дует южный.
Ветер стих. Вздохнули дружно.
Нам урок продолжить нужно.
Слайд 13
Исторические сведения о числе π
Длина окружности тем больше, чем больше ее диаметр.
Для всех окружностей отношение длины окружности к
длине ее диаметра является одним и тем же числом.
Сначала было замечено, что длина любой окружности
примерно в 3 раза больше диаметра. Затем этот результат
был уточнен – в 371 раза, но и тогда
математики знали, что это число
проблем при записях расчетов, ма-
тематики Древней Греции стали
обозначать это число буквой гре-
ческого алфавита – π (пи). Точное значение π не-
известно и сейчас. Нам для вычислений доста-
точно использовать значение π, округленного до
разряда сотых 3,14.
Примерно такую же точность дает значение
π ≈ 22/7. Число 22/7 носит имя великого матема-
тика: называется оно «число Архимеда».
Слайд 14
Двадцать две совы скучали
На больших сухих суках.
Двадцать две
совы мечтали
О семи больших мышах,
О мышах довольно юрких
В аккуратных
серых шкурках.
Слюнки капали с усов
У огромных серых сов.
Шутка из учебника Магницкого
(Для закрепления в памяти рационального выражения числа Архимеда π =22/7 )
Слайд 15
Закрепление новых знаний
Задача
Дано:
Решение:
Окружность С = 2
π r
π ≈ 3,14 С= 2·3,14·4,7 = 29,516 ≈ 29,5 (дм.)
r = 4,7 дм. S = πr²
Найти: S = 3,14·4,7·4,7 = 69,3626 ≈ 69,4 (дм²)
С - ? S - ?
Ответ : длина барьера равна 29,5 дм, площадь
арены равна 69,4 дм².
Задание для групп:
Найти C и S, результат округлить до десятых, если
I II III
r = 5,2 см. r = 6,5 см. r = 3,9 см.
d = 3,8 дм. d = 2,8 дм. d = 5,1 дм.
Слайд 16
Информация о домашнем задании,
инструктаж по его выполнению
Индивидуальное задание:
Придумать ребус или загадку
про окружность или круг
§ 4 п. 24 Проверить на любой модели окружности число π, выполнить все необходимые измерения. Найти длину этой окружности и площадь ограниченного ею круга.
Слайд 17
- можно ли сказать, что:
срез яблока – окружность,
срез теннисного
шарика – окружность,
глобус – окружность?
- приведите свои примеры окружности и круга;
- назовите формулы:
длина окружности,
площадь круга;
что нужно знать, что бы вычислить длину
окружности и площадь круга?
назовите единицы измерения длины,
площади.
Подведение итогов урока
Слайд 18
Я узнал:…
Я запомнил:…
Я научился:…
Мне понравилось:…
Я затруднялся:…
Мое настроение:…
Рефлексия
Я
научился…
Я узнал…
Мне понравилось…
Слайд 20
Результаты урока
Предметные результаты:
в познавательной (интеллектуальной) сфере:
знакомство учащихся с
числом π, расширение
понятия множества чисел;
знакомство учащихся
с формулами длины
окружности и площади круга;
применение формул при решении задач;
в ценностно-ориентационной сфере:
применение знаний при решении практико-
ориентированных задач
Слайд 21
Метапредметные результаты
Познавательные:
сформированность познавательных интересов,
направленных на
развитие представлений о числе π,
длине окружности и
площади круга.
Регулятивные:
- понимание смысла поставленной задачи;
- умение выполнять действия по алгоритму;
умение выполнять учебное действие в соответствии с
целью;
- контроль и оценка процесса и результатов деятельности.
Коммуникативные:
сформированность умений ясно, точно, грамотно
излагать свои мысли в устной речи;
умение адекватно использовать речевые средства
для аргументации своей позиции;
- умение работать в группе в атмосфере сотрудничества.
Слайд 22
Личностные результаты:
готовность и способность обучающихся
к
саморазвитию;
построение продуктивного
взаимодействия в группе,
сотрудничества
в разных ситуациях,
умение не создавать конфликты
и находить выходы из спорных
ситуаций.