- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Погрешности и приближенные числа
Содержание
- 2. ВведениеПри выполнении массовых вычислений важно придерживаться определенных
- 3. Повестка дняСписок изучаемых разделов:Приближенные числа и правила
- 4. ОбзорРазделы лекцииПриближенные числа и правила приближенийПогрешности арифметических операцийОсновные свойства решений
- 5. Словарь терминовПриближенным числом а* называется число, отличающееся
- 6. Приближенные числа и правила приближенийЗначащими цифрами числа
- 7. Приближенные числа и правила приближенийОкругление числа –
- 8. Приближенные числа и правила приближенийОтносительная погрешность (%) чисел с n верными знаками.Начало таблицы.
- 9. Приближенные числа и правила приближенийОтносительная погрешность (%) чисел с n верными знаками.Окончание таблицы.
- 10. Приближенные числа и правила приближенийДля двоичных чисел существуют понятия:Машинный нуль.Машинная бесконечность.Переполнение.Исчезновение порядка. 0Xo-XoМашинная бесконечностьМашинная бесконечностьМашинный нульX-X
- 11. Приближенные числа и правила приближенийЧисла, большие по
- 12. Приближенные числа и правила приближенийПример: Имеется гипотетическая
- 13. Приближенные числа и правила приближенийПроверка точности вычислений
- 14. Приближенные числа и правила приближенийВ представленном примере
- 15. Приближенные числа и правила приближенийВ современной мировой
- 16. Погрешности арифметических операций Погрешности суммы и разности:
- 17. Основные свойства решений Корректность вычислительной задачи. Это
- 18. Скачать презентацию
- 19. Похожие презентации
ВведениеПри выполнении массовых вычислений важно придерживаться определенных простых правил, выработанных практикой, которые позволяют экономить труд вычислителя и рационально использовать вычислительную технику. Одно из таких правил – разработка подробной вычислительной схемы.















Слайд 3
Повестка дня
Список изучаемых разделов:
Приближенные числа и правила приближений.
Погрешности
арифметических операций.
Основные свойства решений.
Время, отводимое на каждый раздел: 5-10
минут.
Слайд 4
Обзор
Разделы лекции
Приближенные числа и правила приближений
Погрешности арифметических операций
Основные
свойства решений
Слайд 5
Словарь терминов
Приближенным числом а* называется число, отличающееся от
точного а и заменяющее последнее в вычислениях. Если известно,
что а*< а , то а* называют приближенным значением числа а по недостатку; если же а* > а, то - по избытку.
Слайд 6
Приближенные числа и правила приближений
Значащими цифрами числа а*
называются все цифры его записи, начиная с первой ненулевой
слева.Значащую цифру числа а* называют верной, если абсолютная погрешность числа не превышает единицу разряда, соответствующего этой цифре.
Пример: Δ (a*) =0, 000002, a* =0, 0103000 – 4 верных цифры.
Слайд 7
Приближенные числа и правила приближений
Округление числа – замена
его другим числом с меньшим числом значащих цифр.
Погрешность
такой замены называется погрешностью округления.Виды округления:
Усечение – отбрасывание всех цифр, расположенных слева от значащей цифры. Абсолютная погрешность не превышает единицы разряда.
Округление по дополнению – при разряде, меньшим 5, остается та же цифра, при большем или равном 5 добавляется 1. Абсолютная погрешность не превышает ½ разряда последней оставляемой цифре.
Границы погрешностей всегда округляют в сторону увеличения.
Слайд 8
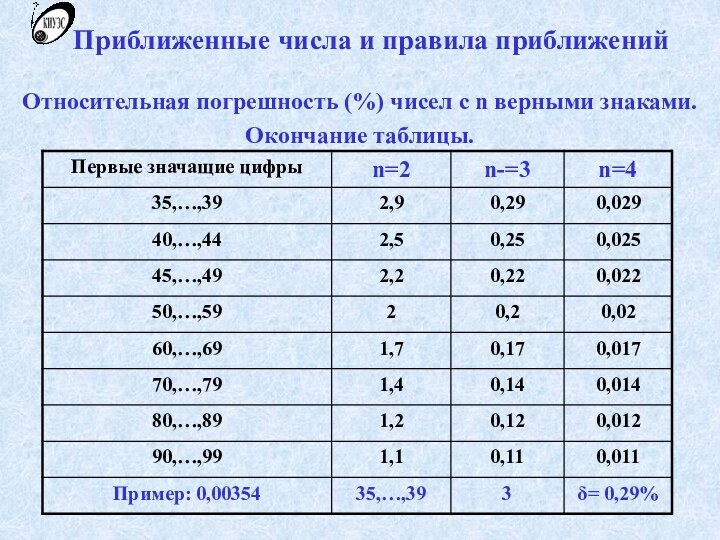
Приближенные числа и правила приближений
Относительная погрешность (%) чисел
с n верными знаками.
Начало таблицы.
Слайд 9
Приближенные числа и правила приближений
Относительная погрешность (%) чисел
с n верными знаками.
Окончание таблицы.
Слайд 10
Приближенные числа и правила приближений
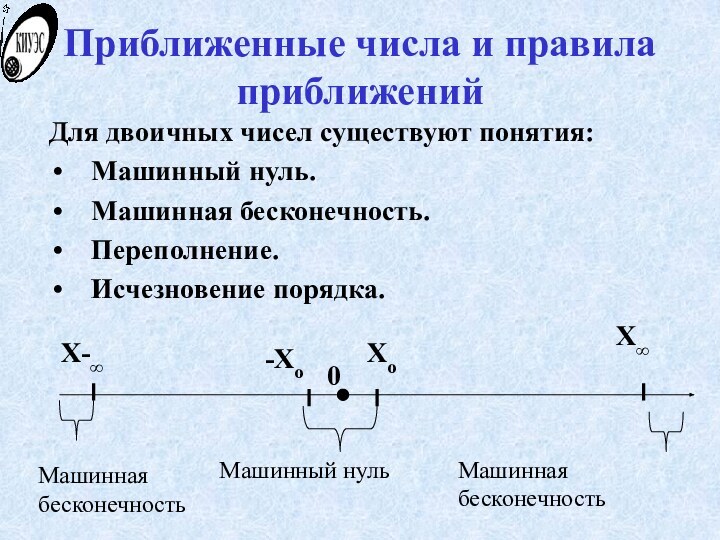
Для двоичных чисел существуют
понятия:
Машинный нуль.
Машинная бесконечность.
Переполнение.
Исчезновение порядка.
0
Xo
-Xo
Машинная бесконечность
Машинная бесконечность
Машинный нуль
X-
X
Слайд 11
Приближенные числа и правила приближений
Числа, большие по модулю,
чем X, рассматриваются, как машинная бесконечность, и попытка получить
такое число приводит к аварийному останову по переполнению. Числа, меньшие по модулю, чем Xo представляются машинным нулем. При получении таких чисел возможно исчезновение порядка (или антипереполнение).Для двоичных чисел при потери точности вычислений используют так называемую удвоенную точность.
Слайд 12
Приближенные числа и правила приближений
Пример: Имеется гипотетическая машина
с 6 двоичными разрядами мантиссы, в которой округление происходит
только по дополнению.Выполнить арифметические действия для двух чисел в двоичном коде:
a=20.5D=10100.1B; b=1.75D=1.11B
a+b=22.25D; a*b=35,785D
a+b=10100.1+1.11=101101.01B ≈10110.1B =22.5D
a*b=10100.1*1.11=1100011.111B ≈100100.1B =36D
Слайд 13
Приближенные числа и правила приближений
Проверка точности вычислений проводится
по так называемому машинному эпсилону εм. Машинный эпсилон εм
– это минимальное из представленных чисел ε, для которых 1 εм > 1Алгоритм проверки (вставка в фрагмент программы):
Задается шаг ε(о)=1, проводится вычисление,
Задается шаг ε(1)=0.5 ε(о) проводится вычисление и проверяется неравенство 1 ε > 1
…………………………………………………………………………………
n. Задается шаг ε(n)=0.5 ε(n-1) проводится вычисление и проверяется неравенство 1 ε > 1
Если неравенство выполняется, то принимается εм= ε(n-1) и переходят к следующему этапу вычислений.
Слайд 14
Приближенные числа и правила приближений
В представленном примере εм
= 0.000001,
т. к. 1+ εм =1.000001, тогда 1
εм =1.00001Если же к 1 добавить любое положительное число ε < εм , то в седьмом разряде результата будет стоять нуль, и после округления получается:
1 ε = 1
Слайд 15
Приближенные числа и правила приближений
В современной мировой практике
используется ошибка вычислений приближенного числа:
Error = |a-a*|/(1+a)
Error→ Δ
(a*) при |a|<<1Error→ δ(a*) при |a|>>1
Слайд 16
Погрешности арифметических операций
Погрешности суммы и разности:
Δ (a*±
b*) ≤ Δ (a*) + Δ (b*)
δ (a*+
b*) ≤ δmax ; δ (a*- b*) ≤ v*δmax δmax = max{δ (a*), δ (b*) }, v=|a+b|/|a-b|
Относительные погрешности произведения и частного: Δ (a*+ b*) ≤ Δ (a*) + Δ (b*)
δ(a* b*) ≤ δ (a*) + δ (b*) + δ (a*) * δ (b*)
δ(a*/ b*) ≤ (δ (a*) + δ (b*))/(1- δ (b*))
Границы относительных погрешностей:
δ(a* b*) ≈ δ (a*) + δ (b*) ≈ δ(a*/ b*)
Слайд 17
Основные свойства решений
Корректность вычислительной задачи.
Это выполнение условий:
1) ее решение y, принадлежащих Y, существует при всех
входных x, принадлежащих X. 2) это решение единственное 3) решение устойчиво по отношению к малым возмущениям входных величин.Единственность вычислительной задачи. Задача должна иметь единственное решение.
Устойчивость вычислительной задачи. Задача устойчива по входным данным, если для любого ε>0 существует
δ= δ(ε)>0 такое, что всякому исходному x* при котором Δ(x*) < δ , соответствует y*, для которого Δ(y*) < ε .
Т. е. решение y зависит от входного x непрерывным образом.
Относительная устойчивость решения – замена Δ на δ.





























