Слайд 2
В социально-экономическом анализе важно знать не только среднее (или
серединное) значение признака, но и насколько равномерно распределены эти
значения относительно среднего значения, а так же знать количественную
меру степени этой неравномерности.
Слайд 3
Вариация (variatio, латинск. - различие, изменение, колеблемость) -
количественное
различие значений одного и того же признака у отдельных
единиц совокупности
позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение
по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию
Слайд 4
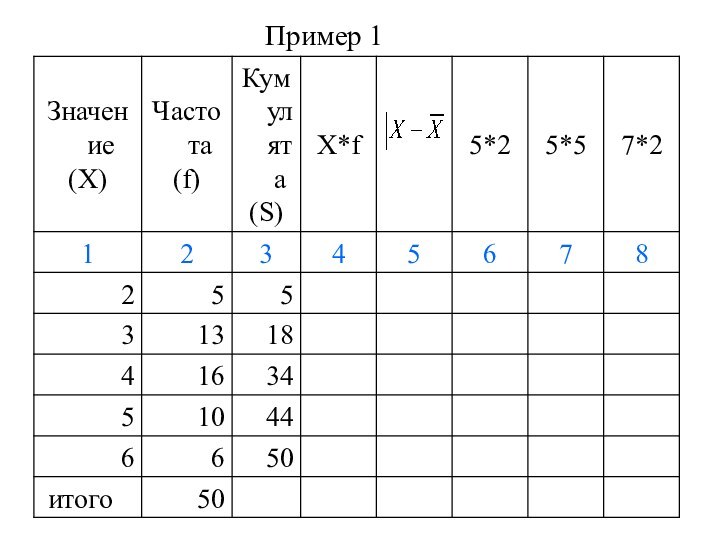
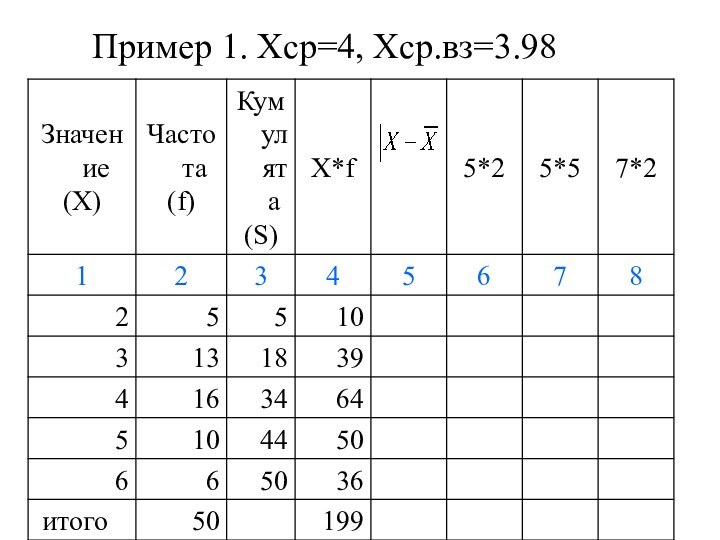
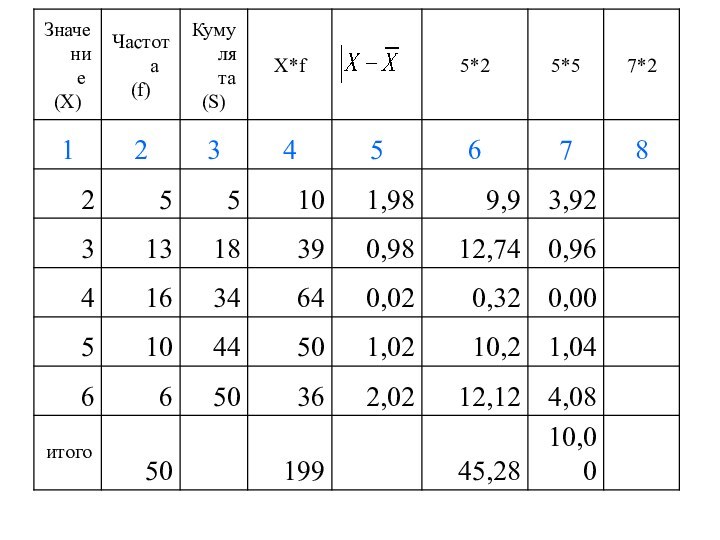
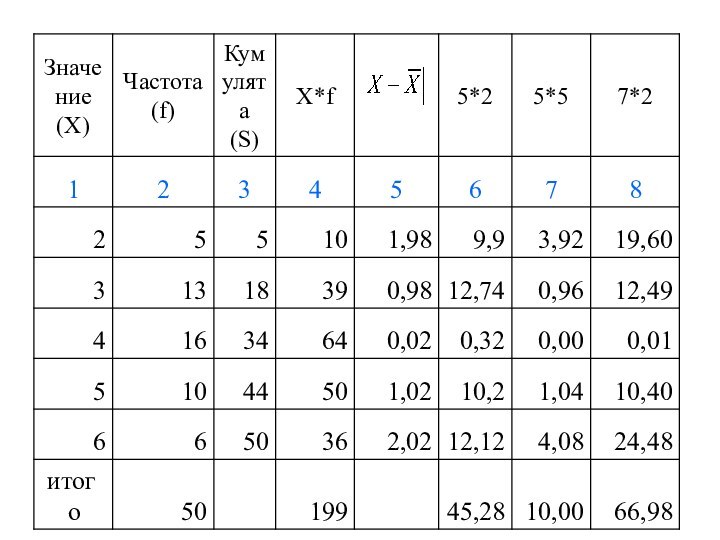
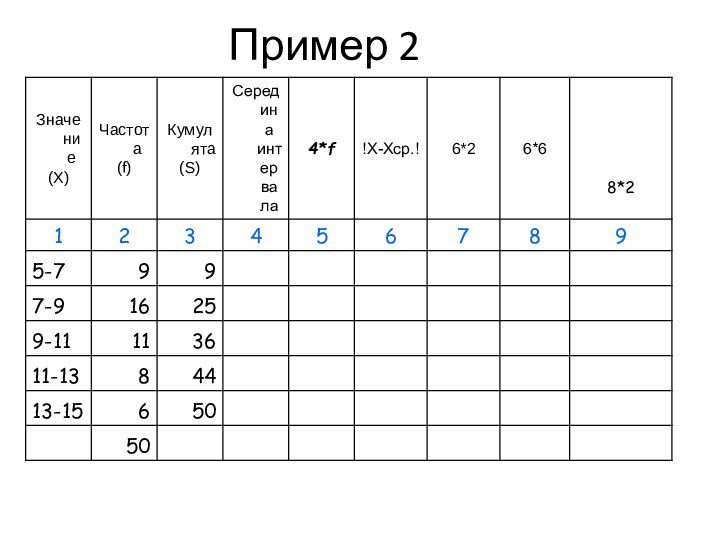
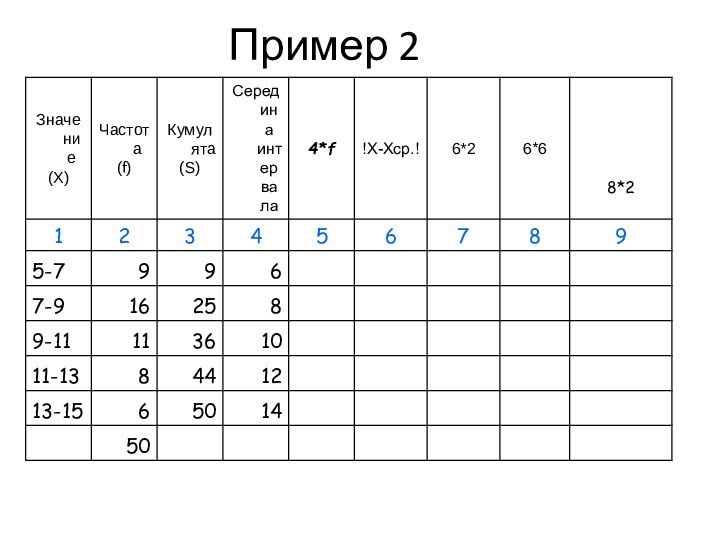
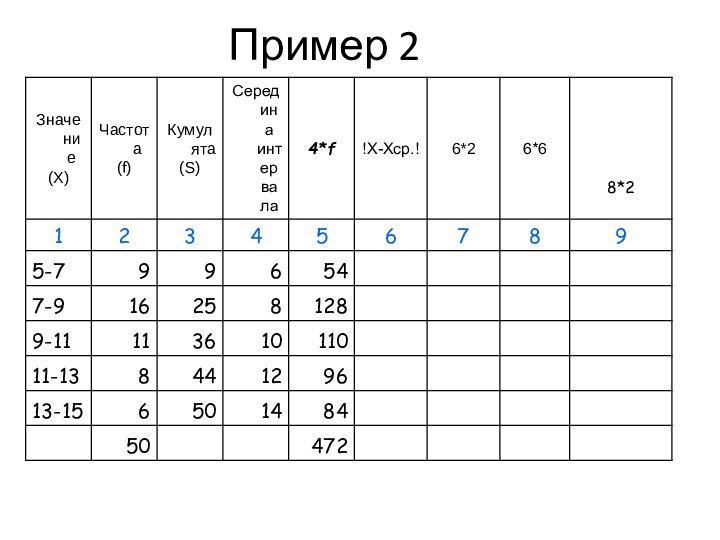
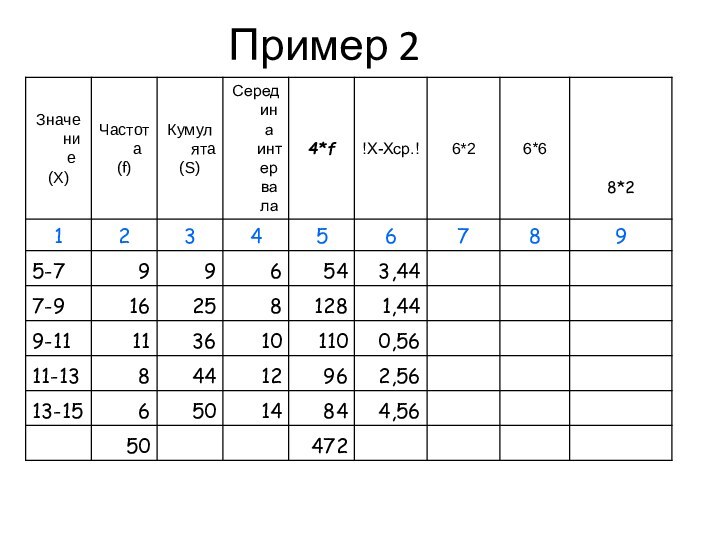
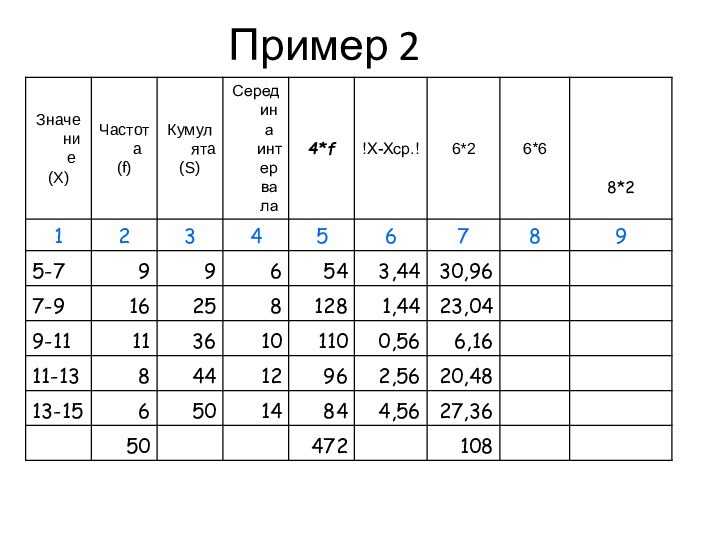
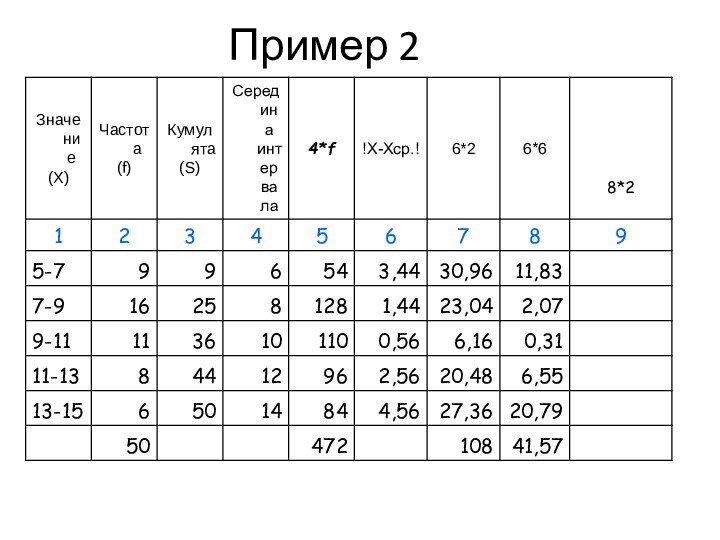
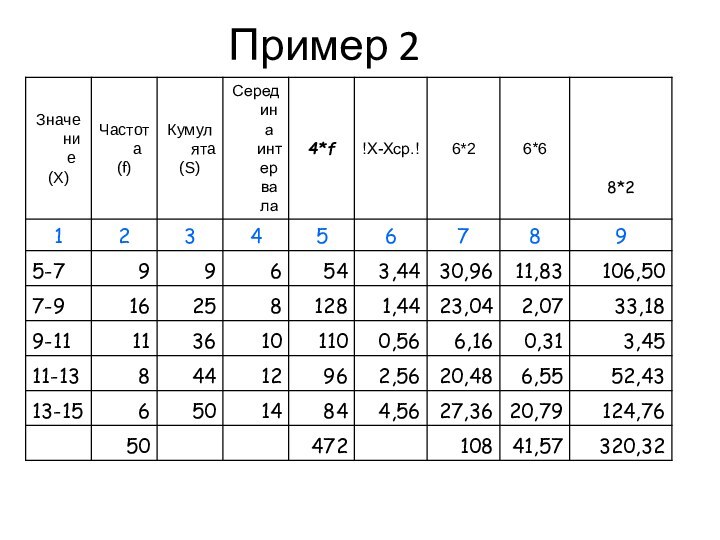
Пример
Пусть заданы два ряда.
Ряд I: 1, 2, 3,
4, 5, 6, 6, 7, 8, 9, 10, 11
Ряд II: 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8
Рассчитаем для этих рядов среднюю арифметическую, моду и медиану.
Ряд I. x = 6, Me= 6, Mo= 6, n= 12 .
Ряд II. x= 6, Me= 6, Mo= 6, n= 12 .
Слайд 5
Закономерность распределения признака в совокупности описывается:
частотными показателями;
показателями распределения
– структурные средние;
показателями степени вариации;
показателями формы распределения.
Слайд 6
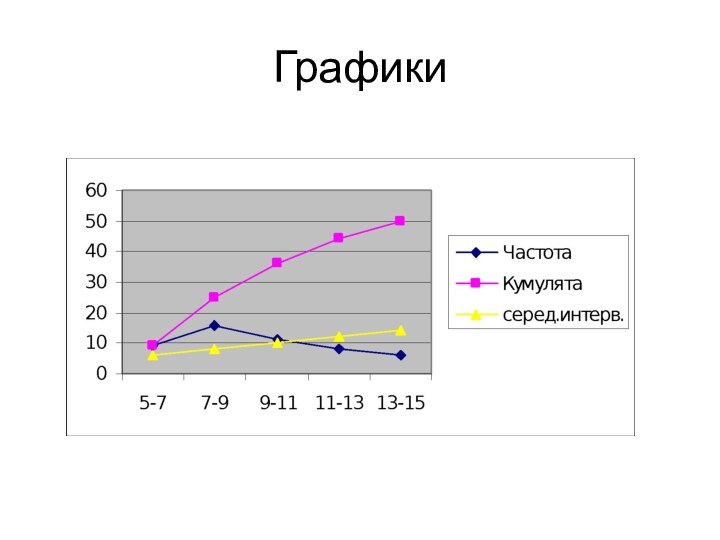
Частотные показатели вариации
абсолютная численность i-той группы –
частота fi
относительная частота – частость di
кумулятивная
(накопленная) частота Si (частость Sd, кумулята) характеризует объем совокупности со значениями вариантов, не превышающих Xi.
S1=f1, S2=f1+f2, S3=f1+f2+f3;
плотность частоты (частости) представляет собой частоту, приходящуюся на единицу интервала,
qi=fi/hi или qi=di/hi
где hi – величина i-того интервала.
Слайд 7
Мо и Ме
В симметричных распределениях средняя арифметическая, мода
и медиана совпадают .
Если это равенство нарушается —
распределение ассиметрично.
Простейшим показателем ассиметрии является разность ,
которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Слайд 8
порядковый номер Ме
при нечетном числе единиц к сумме
всех частот прибавляется единица и все делится на два.
при четном числе единиц медиана = значению признака у единицы совокупности, порядковый номер который определяется по общей сумме частот, деленной на два.
В дискретном ряду распределения медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы
Слайд 9
Изменение вариации признака в совокупности осуществляется с помощью
абсолютных и относительных показателей
Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Слайд 10
Размах вариации -
это разность между максимальным и минимальным
значениями признака
показывает пределы, в которых изменяется величина признака в
изучаемой совокупности
Размах вариации в первом ряду равен 10. Размах вариации во втором ряду равен 4.
Слайд 11
средние показатели вариации, основанные на учете отклонений от
центра ряда распределения - средней арифметической
За отклонение от средней
принимается разность
Для превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю
либо возводить значения отклонений в квадрат
Слайд 12
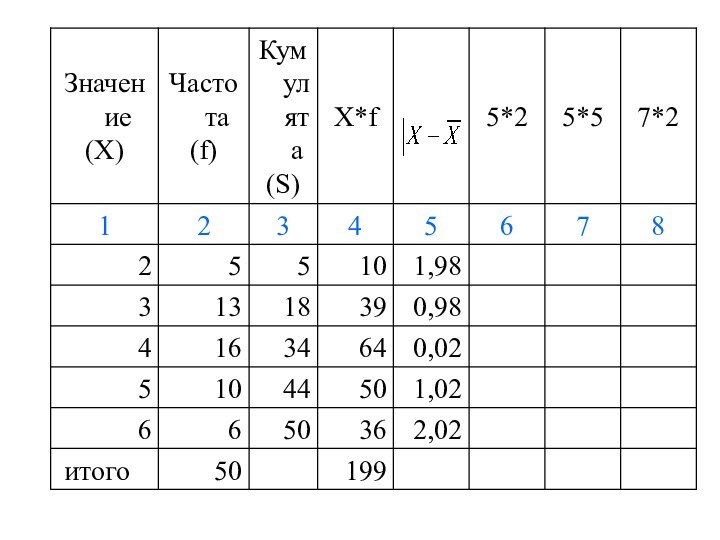
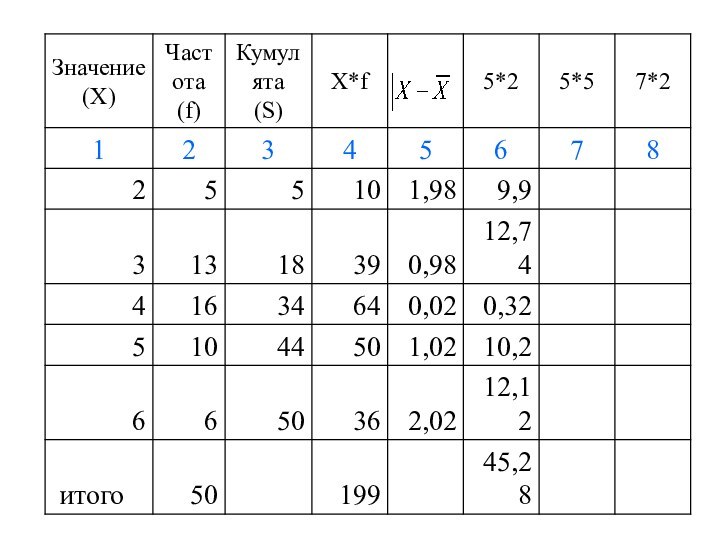
Среднее линейное отклонение
это средняя арифметическая из абсолютных отклонений
отдельных значений признака от средней; показывает, насколько в среднем колеблется величина
признака у единиц исследуемой совокупности.
Среднее линейное отклонение простое:
Среднее линейное отклонение взвешенное:
Слайд 13
Среднее квадратическое отклонение показывает во сколько раз в
среднем колеблется величина признака совокупности; является мерой надежности средней
величины: чем оно меньше, тем точнее средняя арифметическая.
Средняя квадратическая простая
Средняя квадратическая взвешенная
Слайд 14
Опыт работы у пяти претендентов на работе
составляет: 2,3,4,7
и 9 лет.
Хср.=5 лет
Слайд 15
Дисперсия - средний квадрат отклонений индивидуальных значений признака
от его средней величины (1- дисперсия взвешенная, 2- дисперсия
простая)
средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней
Слайд 16
Если из генеральной совокупности сделать несколько выборок и
каждый раз при этом определять среднее значение признака, то
возникает задача оценки колеблемости средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле
σ2 (Х) = σ2 /n
где n - объем выборки; σ2 - дисперсия признака, рассчитанная по данным выборки.
Слайд 17
Для оценки достоверности результатов выборочного наблюдения применяется показатель
средней ошибки выборки
Величина
носит название средней ошибки выборки и является
характеристикой отклонения выборочного среднего значения признака Х от его истинной средней величины
Слайд 18
Свойства дисперсии:
Дисперсия постоянной величины равна 0.
Если
все значения вариантов признака X уменьшить на постоянную величину
А, то дисперсия не изменится.
Если все значения вариантов Х уменьшить в К раз, то дисперсия уменьшится в К2 раз.
4.При малом числе наблюдений (< 30):
Слайд 19
Сравнение вариации нескольких совокупностей по одному и тому
же признаку, а тем более по различным признакам с
помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней
Слайд 20
Относительные показатели вариации -
Слайд 21
Коэффициент осцилляции – это отношение размаха вариации к средней,
в процентах. Отражает относительную колеблемость крайних значений признака вокруг
средней.
Линейный коэффициент вариации характеризует долю усредненного значения абсолютного отклонения от средней величины.
Слайд 22
Коэффициент вариации позволяет судить об однородности совокупности:
–
однородная;
– 17–33%% – достаточно однородная;
– 35–40%% – недостаточно однородная;
– 40–60%% – это говорит о большой
колеблемости совокупности.
Слайд 23
Рассчитать коэффициент вариации на основе среднего квадратического отклонения
для следующего примера:
Расход сырья на единицу продукции составил (кг):
по одной технологии Х1ср.=10 при σ1=4; по другой-
Х2ср.=6 при σ2=3.
Какая вариация расхода сырья интенсивнее?
Слайд 42
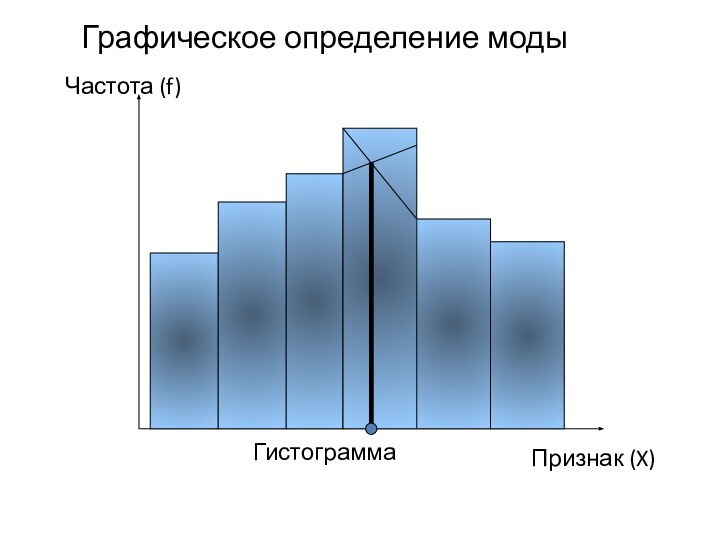
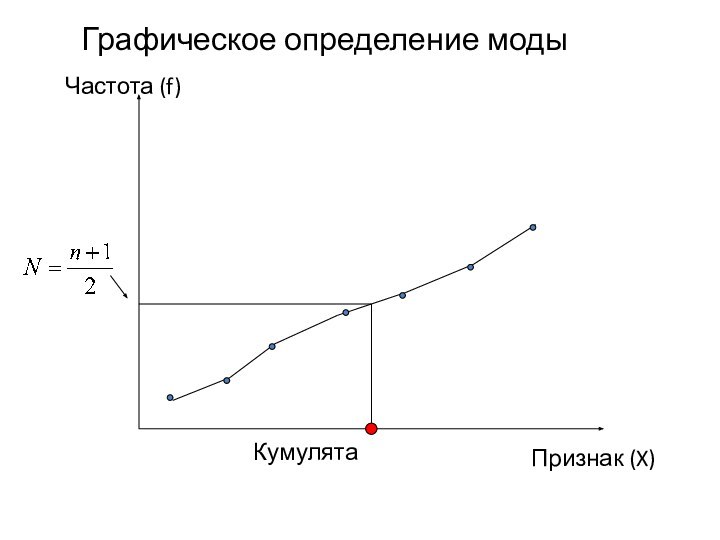
Графическое определение моды
Гистограмма
Частота (f)
Признак (X)