Презентация на тему Понятие бесконечной интегральной суммы. Интеграл

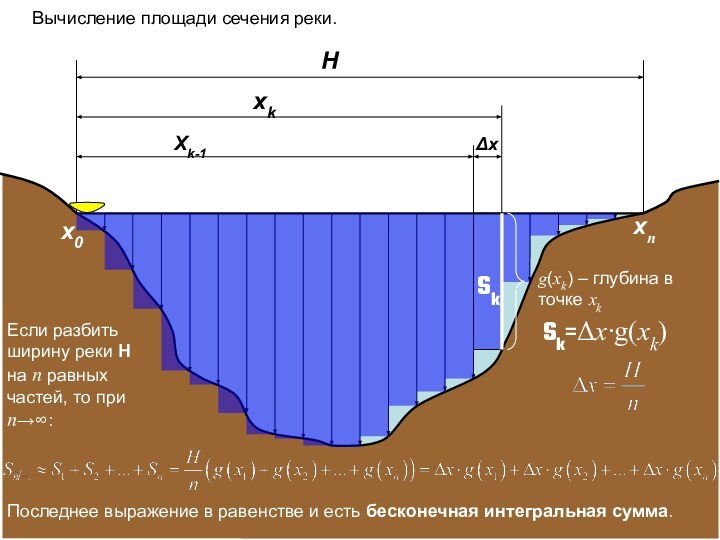
xk
Если разбить ширину реки H на n равных частей,

Sk=Δx∙g(xk)

x0

xn

Последнее выражение в равенстве и есть бесконечная интегральная сумма.

различных пространственных фигур, попробуем найти объем лимона. Ни на

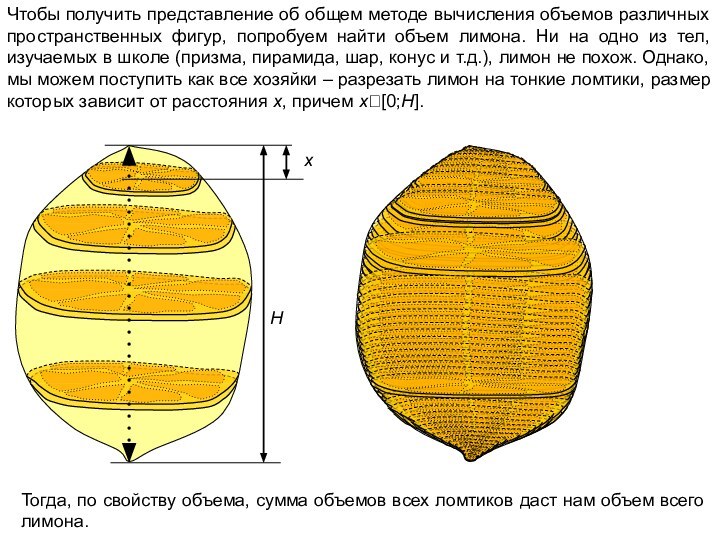
H

x

Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.

фигуры плоскостями, перпендикулярными оси фигуры; причем, если принять число

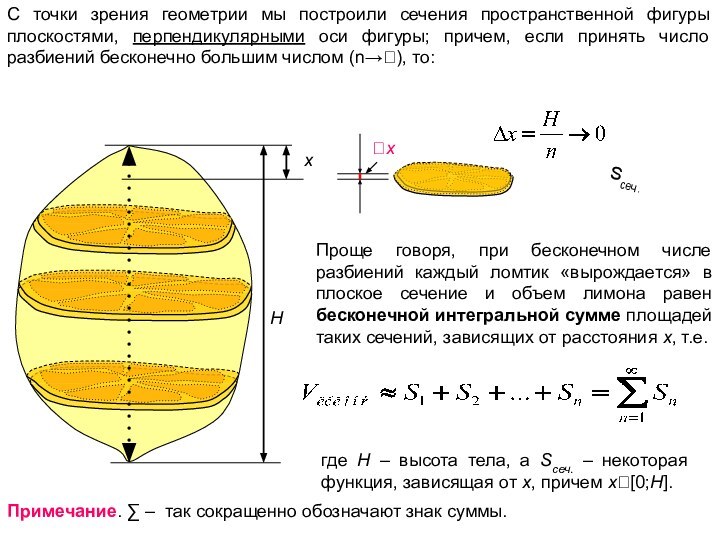
Проще говоря, при бесконечном числе разбиений каждый ломтик «вырождается» в плоское сечение и объем лимона равен бесконечной интегральной сумме площадей таких сечений, зависящих от расстояния x, т.е.

где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x[0;H].

Sсеч.

Примечание. ∑ – так сокращенно обозначают знак суммы.

данный пример и вывод окончательной формулы объёма прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен бесконечной интегральной сумме площадей сечения (равных площади основания) на промежутке [0; H] (взятых вдоль высоты).

значения:
y=f(x)
a
x0=

в отрезок, длина которого равна значению функции (или его

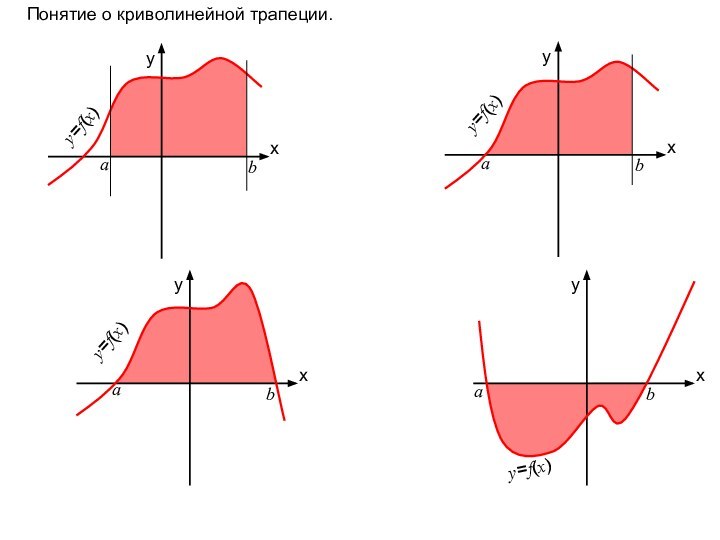
y=f(x)

a

x0=

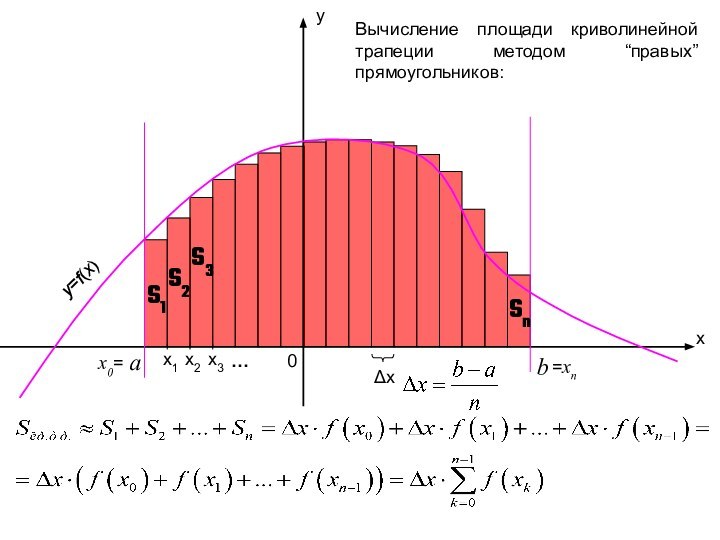
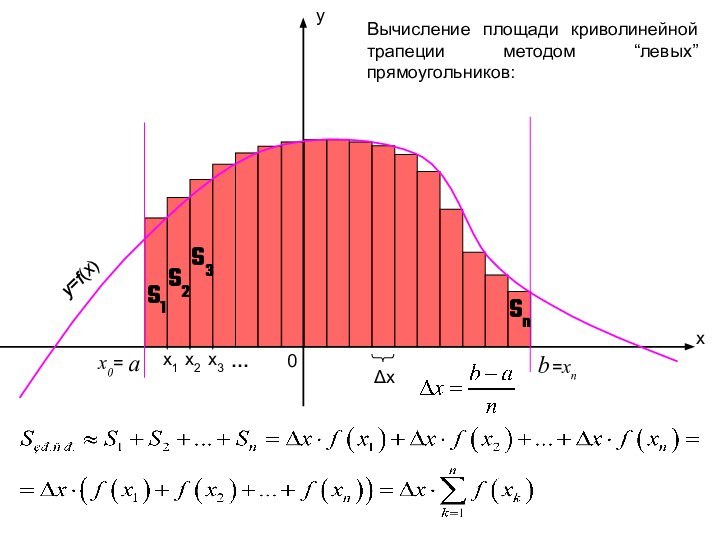
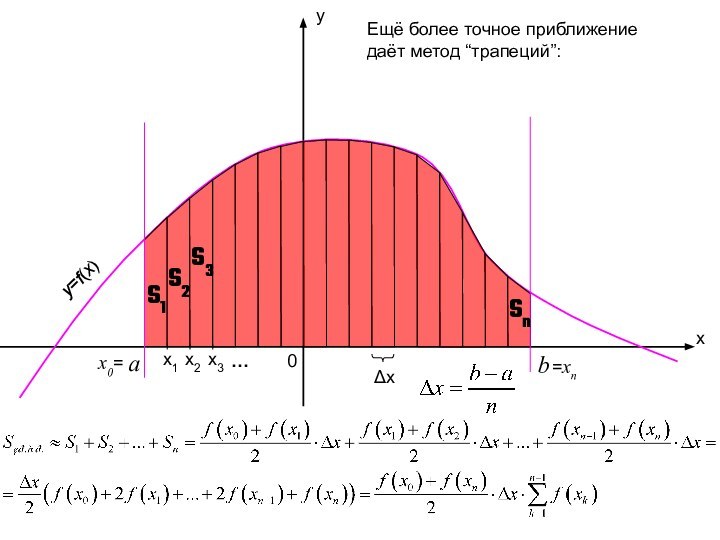
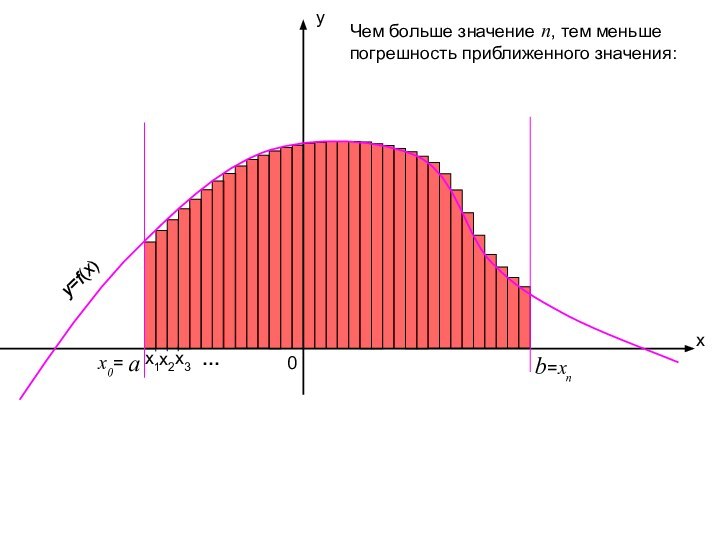
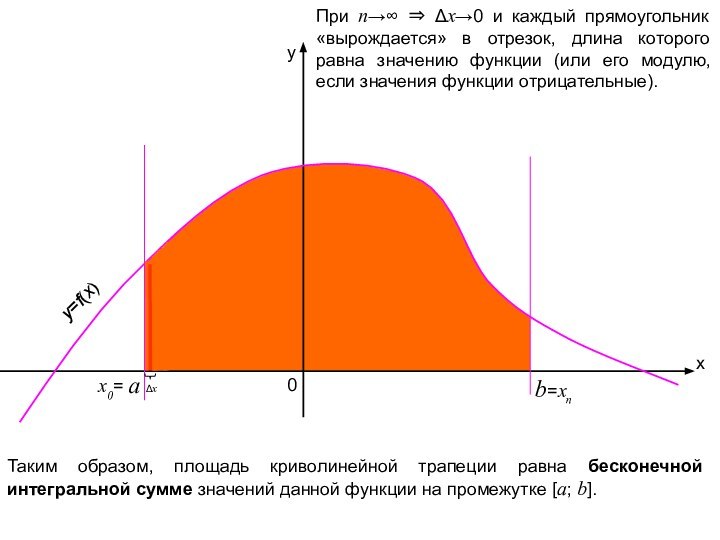
Таким образом, площадь криволинейной трапеции равна бесконечной интегральной сумме значений данной функции на промежутке [a; b].

Δx

трапеции с помощью понятия бесконечной интегральной суммы значений данной

Примечание. Обратите внимание, что знак интеграла напоминает стилизованную букву S, что естественно из геометрического смысла этого понятия.

Читают: интеграл от a до b эф от икс дэ икс.

Число a называют нижним пределом интегрирования, b – верхним пределом интегрирования, f(x) – подынтегральной функцией, x – переменной интегрирования.

Если Вы владеете понятием предела (lim), то можно дать следующее определение интеграла:

, где xn[a; b].

ΔS
Δx
b
a
x+Δx
x
Возьмём теперь прямоугольник такой же площади ΔS, опирающийся на

c

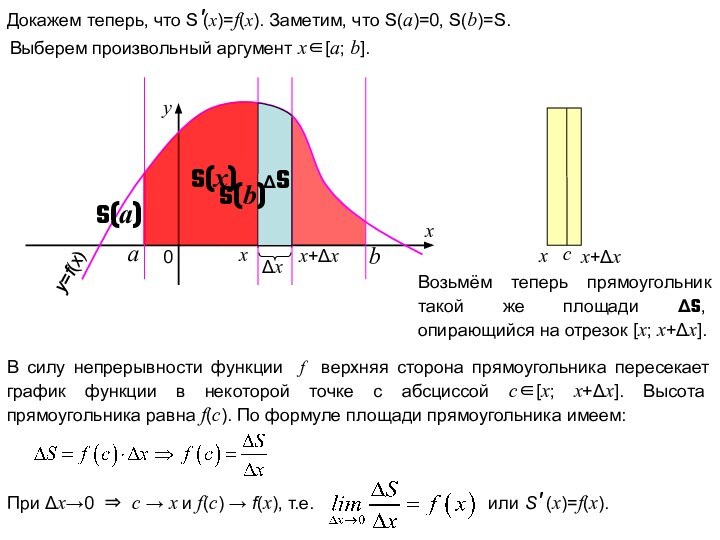
В силу непрерывности функции f верхняя сторона прямоугольника пересекает график функции в некоторой точке с абсциссой c[x; x+Δx]. Высота прямоугольника равна f(c). По формуле площади прямоугольника имеем:

S(x)

Выберем произвольный аргумент x[a; b].

S(a)

S(b)

(если, например, на заданном промежутке значения функции отрицательны).

(объясните их с помощью учителя):
Применение этих свойств часто упрощает

, где c