человек пытался постичь и создать порядок, красоту и совершенство”
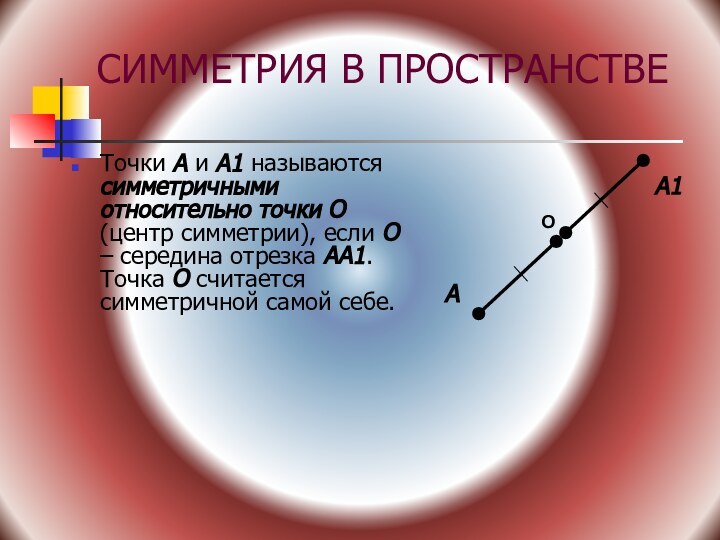
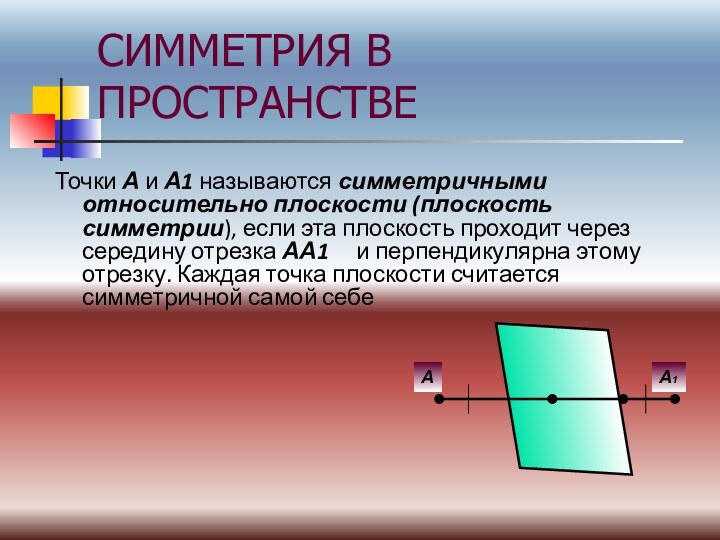
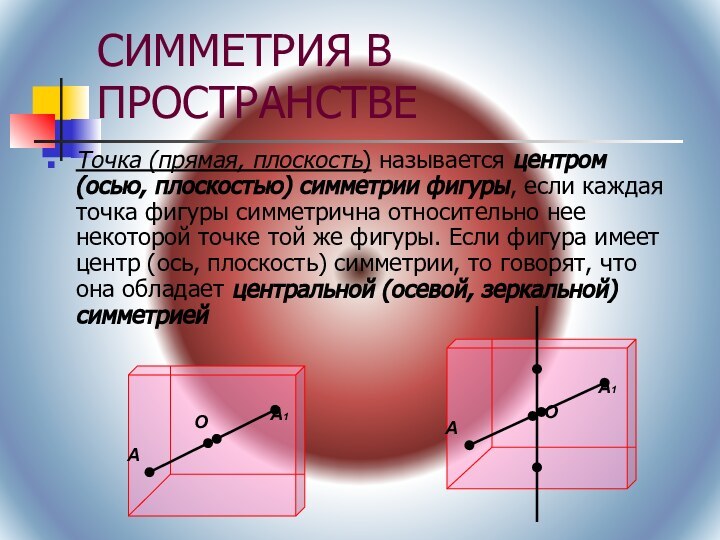
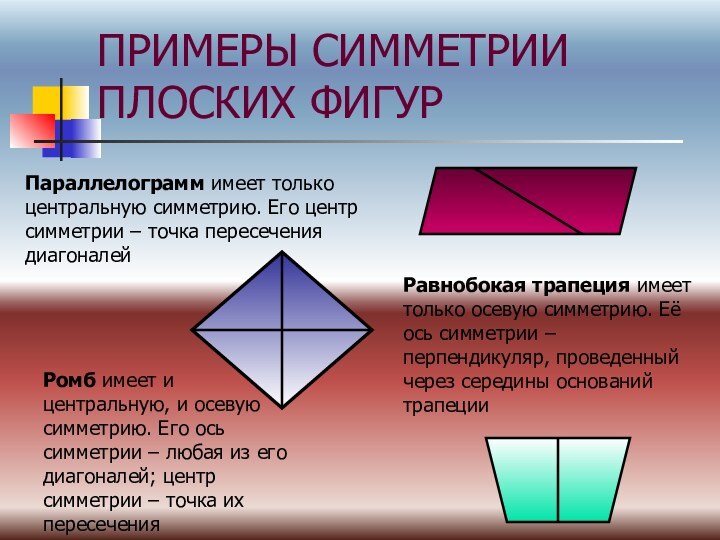
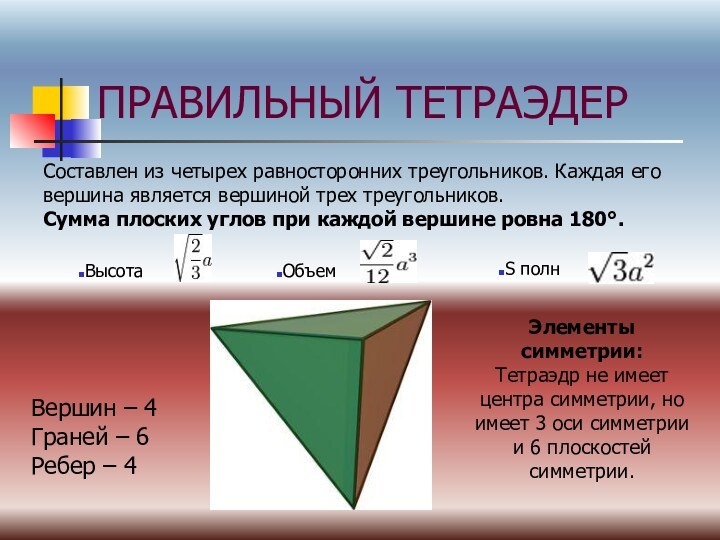
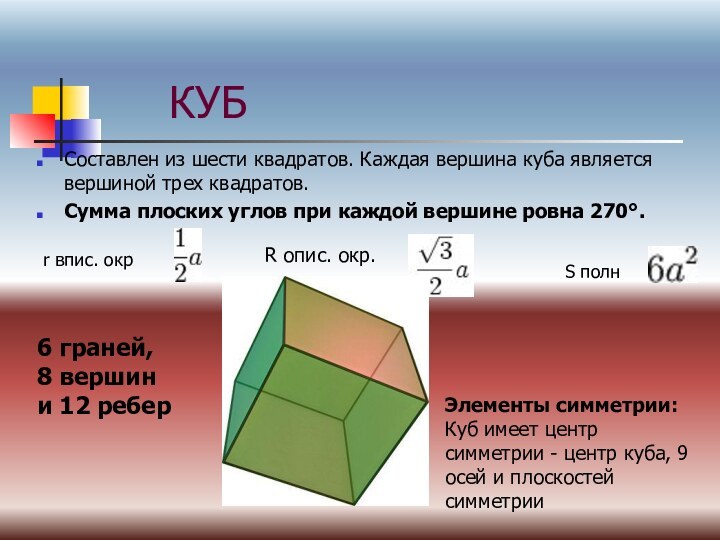
(Г.Вейль)Симметрия («соразмерность») — соответствие, неизменность (инвариантность), проявляемая при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы, сохраняя одну точку на месте.
«Витрувианский человек»
Ленардо Да Винчи (1490,Венеция)